Побудова множини цілих чисел

Розширення множини N здійснюється приєднанням до неї від'ємних цілих чисел і числа 0.

Означення 1. Від'ємним цілим числом називають число виду — п (читають: «мінус п»), де п Є N. Множину від'ємних цілих чисел позна­чають Z.

Після введення від'ємних цілих чисел, натуральні числа природно назвати додатними цілими числами. Для множини додатних цілих чисел, крім позначення N застосовують позначення Z₊. Отже, Z₊ ~ Z_- Означення 2. Об'єднання множин Z₊, Z_- і {0} називають множи­ною цілих чисел і позначають Z, тобто

Z=Z₊UZ_-U{0}, причому множини Z₊, Z_- і {0} попарно не перетинаються.

Надалі для зміни чисельності при переході А→В вживатимемо позначення ∆А→в (читають: «дельта переходу від А до В»). Введення Множини Z дає змогу записати

п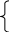 (В) — п(А), якщо п(А)<п(В)\

∆ A→B = 0, якщо п(А) = п(В)\

—(n(A) —n(В)), якщо п(А)>п(В),

тобто зміна чисельності при будь-якому переході А→ В є певним ці­лим числом, що визначається чисельностями множин А і В.

Таким чином, запис ∆A→B = а (∆A→B = —а), де а Є N. означає, що при переході А → В чисельність збільшилась (зменшилась) на а; запис ∆A → B = 0 означає, що при переході А→В чисельність зали­шилась без зміни. Розглянемо ще деякі означення, що стосуються цілих чисел.

Додатне ціле число а та від'ємне ціле число —а називають проти­лежними, причому — (—а) = а. Наприклад, — (—5)= 5. Число 0 вважають протилежним самому собі, —0 = 0.

Буквами без знака позначають не тільки додатні, а й від'ємні цілі числа та нуль. Тоді та сама буква зі знаком мінус означає протилежне ціле число. Наприклад, якщо а = 5, b = —4, с = 0, то —а = —5, —b = 4, — с = 0.

Два цілі числа називають числами одного і того самого знака, або говорять, що знак одного з них збігається зі знаком другого, якщо вони обидва або додатні, або від'ємні. Наприклад, —7 і —11 — числа одного й того самого знака.

Два цілі числа називають числами різних знаків, якщо одне з них додатне, а друге — від'ємне. Наприклад, —8 і 5 — числа різних знаків.

Модулем (абсолютною величиною) цілого числа а називають число (позначають | а | і читають «модуль а»), яке визначається рівностями

xa, якщо а Є Z ₊ U {0};

|a| =

x — а, якщо а Є Z _-

Наприклад, | 5 | = 5, | —17 | = 17.

Зображення цілих чисел на числовій прямій

На горизонтальній прямій р (рис. 45) візьмемо дві точки: точку О і справа від неї — точку А_г. Точку О називають початком відліку, а А₁ — одиничною точкою. Відрізок ОА_г називають одиничним від-

n' An' A'₂ A'₁ 0 A₁ A₂ A_n

- n -2 -1 0 1 2 n n p

різком, а напрямок р від точки 0 до точки А₁ — додатним напрямком. Означення 3. Пряму р з вибраними на ній точкою О — початком відліку, точкою А₁ — одиничною точкою і додатним напрямком від точки О до точки А± називають числовою або координатною прямою.

Множину Z можна зобразити точками числової прямої.

Уздовж променя h = OA, який називають додатним, починаючи від точки А1, послідовно відкладатимемо відрізки, кожен з яких має Довжину одиничного відрізка. Кінцеві точки утворюваних при цьому відрізків позначимо буквами A2, A3, ..., Аn. Тоді довжина'відрізка ОАп дорівнює п довжинам одиничного відрізка. При нескінченному продовженні цього процесу утворюється промінь h з виділеною на ньому нескінченною множиною точок M+ = {А1, А2,…, An,…}, яка еквівалентна множині натуральних чисел N = {1, 2, ..., n, ...}. Закон відповідності Аn ↔ n. При цьому число п називають координатою точки Аn. На рис. біля кожної точки множини M+ записано її координату.

Промінь h з побудованими на ньому точками множини М+ ілюструє відомі властивості множини N.

Промінь h', що доповнює додатний промінь h до прямої р, називають від'ємним.

До додатного променя h з побудованою на ньому множиною точок М+ застосуємо перетворення симетрії відносно початку відліку. В ре-вультаті дістанемо від'ємний промінь h' і на ньому нескінченну множину точок М_ = {A'1, A'2, ..., А'n, ...}, де кожна точка А'n симетрична відповідній точці Ап з множини М+. Множина точок М_ еквівалентна множині від'ємних цілих чисел Z_ = {—1, —2, ..., —n, ...). Закон відповідності зрозумілий: А'n ↔ —n. При цьому число —п назвемо координатою точки А'n. На рис. біля кожної точки множини М— записано ЇЇ координату.

Початку відліку поставимо у відповідність як координату — число

0. На рис. точка О має координату 0.

Множину М, що визначається рівністю М = М+ U М- U {0}, називають множиною цілочисельних точок числової прямої.

Множина М є геометричним зображенням множини Z. Якщо цілому числу к відповідає цілочисельна точка К, то останню називають зображенням числа к на числовій прямій.