Множина раціональних чисел

Дроби і на основі їх додатні раціональні числа були введені для того, щоб мати змогу виражати числом довжину будь-якого відрізка, сумірного з одиничним відрізком. Додатні раціональні числа характе­ризують також збільшення довжини при заміні одних відрізків інши­ми (зазначені відрізки сумірні з одиничним відрізком). Щоб охарак­теризувати зменшення довжини, вводять від'ємні раціональні числа аналогічно тому, як були введені від'ємні цілі числа.

Означення 22. Від'ємним раціональним числом називають число виду —а, де а Є Q₊ Множину від'ємних раціональних чисел позна­чають Q_-_.

За цим означенням Q₊ ~ Q_-_.

Означення 23. Об'єднання множин Q₊, Q_- i _ 1 {0} називають мно­жиною раціональних чисел і позначають Q. Таким чином, Q = Q₊ Q_- {0}, причому множини Q₊, Q_- і {0} попарно не перетина­ються.

Зрозуміло, що Z Q.

Додатне раціональне число а і від'ємне раціональне число —а називають протилежними, причому вважають, що — (—а) = а.

Число нуль вважають протилежним самому собі. Надалі буквами без знака позначатимемо не тільки додатні, а й від'ємні раціональні числа та нуль. Тоді та сама буква зі знаком мінус означатиме проти­лежне раціональне число.

Модулем (абсолютною величиною) раціонального числа а назива­ють число (позначають | а |), яке визначається рівностями

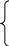а, якщо а Є Q₊ {0},

|a|

— а, якщо а Є Q_-

Раціональні числа можна зображати точками числової прямої ана­логічно тому, як це було зроблено вище для цілих чисел. Узагальнен­ням відповідних означень для цілих чисел є наступне означення.

Означення 24. Говорять, що раціональне число а дорівнює раціо­нальному числу b (записують а = b), якщо а і b•— числа одного знака та | а | = | b |, або а = 0 і b = 0.

Говорять, що раціональне число а менше від раціонального числа b (записують а < b), якщо для чисел а і b виконується одне із спів­відношень:

1)а,bЄQ₊+і а < b,

2. а, Ь Є Q_-_ і | а | > | b |,

3. а Є Q_-, b Є Q₊ {0},

4. а Є Q_- {0}, b Є Q₊.

Можна показати, що множина (Q, <) лінійно впорядкована, щільна і необмежена як зверху, так і знизу.

Раніше (див. п. 1.3) було встановлено, що множина Q — зчис-ленна.

На раціональні числа повністю переноситься означення суми й різ­ниці цілих чисел (там, де йшлося про зміну чисельності, йдеться про зміну довжини); операції додавання й віднімання раціональних чисел мають такі самі властивості, що й для цілих чисел.

Добутком раціональних чисел а і b називають раціональне число

с = аb, модуль якого дорівнює b — числа одного знака, і від'ємне — в противному разі. Для будь-якого раціонального числа а маємо

а • 0 = 0 • а = 0.

Це означення є перенесенням на раціональні числа відповідного означення для цілих чисел. Операція множення раціональних чисел має такі самі властивості, що й для цілих чисел.

Операцію ділення раціональних чисел розглядають як обернену до множення. Ділення можливе тоді і тільки тоді, коли дільник від­мінний від нуля. Останнє твердження наводимо без доведення.

Всі перелічені операції у множині Q є узагальненнями відповід­них операцій у множині Q₊.