Додавання десяткових дробів

Правило додавання десяткових дробів:

для того щоб додати два десяткові дроби, треба

1. зрівняти у дробів кількість цифр справа від коми;

1. відкинути в дробах коми і додати утворені при цьому натуральні числа;

2. у сумі відокремити комою справа стільки цифр, скільки відокрем­ лено в кожному з доданків.

На практиці, додаючи дроби, кількість цифр після коми можна не зрівнювати і коми не відкидати, а підписати дроби один під одним так, щоб кома була під комою, і додавати числа так само, як натураль­ні числа. Результат буде той самий (чому?). Наприклад,

128,71

35,648

164,358.

Так само виконується віднімання десяткових дробів:

__ 571,3485

93,539

477,8095.

Зазначимо, що в попередніх прикладах нулі не дописувалися, але дії виконуються так, ніби ці нулі було дописано.

Правило множення десяткових дробів: для того щоб перемножити два десяткові дроби, треба

1. відкинути в записах цих дробів коми;

2. знайти добуток двох утворених натуральних чисел;

1. у добутку відокремити комою справа стільки цифр, скільки їх відокремлено в обох множниках разом.

Ділення десяткових дробів. Нехай маємо два десяткові дроби

a = a_n a_n-1 … a₀, b₁ b₂ … b_k, c = c_m c_m-1 … c₀, d₁ d₂ … d_k

(для зручності дроби зведені до спільного знаменника). Частку e = а : о знайдемо за правилом ділення звичайних дробів:

e =

Таким чином, частку двох десяткових дробів зображено звичайним дробом. Виникає запитання: коли частку двох десяткових дробів можна зобразити у вигляді десяткового дробу? Відповідь залежить від можливості перетворення звичайного дробу в десятковий. Питання про можливість такого перетворення буде розглянуто далі. Виявля­ється, що не кожний звичайний дріб можна перетворити у десятковий; зокрема, частку двох десяткових дробів не завжди можна записати у вигляді десяткового дробу.

Тому розглянемо питання про перетворення десяткових дробів у звичайні і навпаки — звичайних дробів у десяткові.

Зрозуміло, що кожний десятковий дріб можна замінити звичайним дробом (зокрема, нескоротним), що дорівнює йому.

Справді, це випливає з означення десяткового дробу. Так,

1,25 = 1 ;

0,424 =

0,17 = .

Розглянемо тепер перетворення звичайного дробу у десятковий. Повну відповідь на це питання дає наступна теорема.

Теорема 30. Для того щоб звичайний нескоротний дріб пере­творювався у десятковий, необхідно і достатньо, щоб канонічний роз­клад його знаменника містив лише прості множники 2 і 5.

Доведення. Необхідність. Нехай нескоротний дріб можна

зобразити десятковим дробом: Тоді т • 10^k = nq. Якщо

б канонічний розклад числа п містив просте число р, відмінне від 2 і 5, то т • 10^k ділилося б на р. Але 10* не ділиться на р. Тому Д (10^k,

p) = 1. Отже, число т ділиться на р і дріб є скоротним. Зайшли

у суперечність, бо дріб - нескоротний. Це протиріччя показує,

що до канонічного розкладу знаменника п не можуть входити прості множники, відмінні від 2 і 5.

Достатність. Нехай — нескоротний дріб і п = 2^α5^β, де α і

β — невід'ємні цілі числа, з яких принаймні одне відмінне від нуля. Тоді

=

а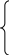 тому

якщо α = β,

= якщо α < β,

якщо α > β,

що й треба було довести.

Один із способів перетворення звичайного дробу у десятковий міститься в доведенні останньої теореми, а точніше, в доведенні до­статності ЇЇ умови.

Інший спосіб перетворення звичайного дробу у десятковий поля­гає в діленні чисельника на знаменник.

Нехай дріб може бути перетворений у десятковий: = .

Тоді m • 10^k = nq. Звідси (т • 10^k) п і q є часткою від ділення т х x 10^k на п. Тому для перетворення дробу у десятковий треба до

чисельника дописати k нулів і здобуте число розділити на знаменник, а в частці відокремити комою к нулів. На практиці виконують ділен­ня чисельника на знаменник, дописуючи до чисельника нулі по одно­му доти, поки ділення не закінчиться.