38

Математика

5 семестр

ЗАСТОСУВАННЯ ТЕОРІЇ МНОЖИН І МАТЕМАТИЧНОЇ ЛОГІКИ ДО

ОЗНАЧЕННЯ ПОНЯТЬ ШКІЛЬНОГО КУРСУ МАТЕМАТИКИ

Тема. РІВНЯННЯ, НЕРІВНОСТІ, ФУНКЦІЇ

ВИРАЗИ

1. Числові вирази

Поняття виразу, числових рівностей і нерівностей, рівняння і нерівності зі змінними, їх системи і сукупності широко застосовуються в різних науках, тому їх вивченню приділяється велика увага. Всі ці поняття можуть бути по-різному означені. Серед них найбільш простими і науково точними є ті, що базуються на використанні теорії множин і математичної логіки.

Під числовим виразом розуміють запис чисел та операцій над ними, в якому за попередньою домовленістю відомий порядок виконання операцій над ними. Кожне число є також числовим виразом. Числа виразу називаються його компонентами.

Порядок операцій у числовому виразі регулюється круглими дужками: спочатку операції виконуються у найглибших дужках, потім у наступних і т.д., зовнішні дужки опускаються. Якщо ж дужки в числовому виразі відсутні, то порядок виконання арифметичних операцій такий: множення або ділення, потім додавання або віднімання в порядку їх запису.

Говорячи про числові вирази, мають на увазі, що результати зазначених у них операцій існують, тобто операції виконувані. Але якщо в числовому виразі є, наприклад, операція ділення з дільником, рівним нулю, то її результат не існує. В цьому разі кажуть, що числовий вираз не має смислу. Зокрема, числовий вираз (4 + 5) : (6 – 2  3) не має смислу, бо при виконанні зазначених операцій у ньому з’являється необхідність ділення на нуль.

Якщо в числовому виразі виконати всі зазначені операції, то одержане число називається його значенням. Якщо числовий вираз є числом, то це число і називається його значенням. Залежно від значень числові вирази поділяються на додатні, від’ємні і нульові, записується це так: А > 0, А < 0, А = 0. Числові вирази не завжди мають значення в тій числовій множині, з якої беруть їх компоненти. Наприклад, числовий вираз 15 : (4 – 7) не має значення у множині натуральних чисел, бо різниця чисел 4 і 7 не має значення у множині натуральних чисел. Хоча компоненти і значення виразів (3 – 8) + (14 – 3) і ((1 + + 8) : 18)  6 є натуральними числами, але їх не можна розглядати над множиною натуральних чисел, бо результати проміжних операцій і не є натуральними числами. Це пояснюється тим, що не всі операції є виконуваними над певними числовими множинами. При розгляді числових виразів в усіх випадках, коли не вказано, з яких числових множин беруться їх компоненти, мають на увазі множину дійсних чисел.

Числовим виразам при потребі дають назви за останніми в них операціями. Наприклад, вираз 4 + 36 : 9 називають сумою числа 4 і частки чисел 36 і 9.

Числові вирази не є висловленнями, бо про них не можна сказати, істинні вони чи хибні. Домовимося позначати числові вирази великими латинськими буквами, а множину всіх виразів – W.

З числовими виразами знайомляться вже учні початкових класів. Спочатку з виразами виду 5 + 3, 8 – 2, називаючи їх відповідно сумою і різницею. Потім розглядаються числові вирази дедалі складнішої структури. Терміни "математичний вираз", "значення виразу" з’являються в лексиконі учнів, коли вони вже виконують обчислення в межах сотні. В процесі навчання учні знаходять значення числових виразів; записують розв’язок, коли це можливо і є потреба, текстової задачі у вигляді числового виразу; складають за даними виразами задачі. При виконанні таких завдань вони неминуче зустрічаються з числовими виразами, значення яких не можна знайти у множині натуральних чисел. Наприклад, про вираз 4-7 учні говорять, що його значення не можна знайти, бо не можна від меншого числа відняти більше.

2. Числові рівності та їх властивості

Два числових вирази називаються рівними, якщо рівні їх числові значення. Відношення рівності на множині числових виразів є відношенням еквівалентності, бо таким воно є для числових множин, а тому визначає розбиття на класи рівних між собою виразів. Це дає змогу в усіх випадках, коли цікавляться значенням виразу, а не його структурою, заміняти один вираз на рівний йому. Наприклад, вираз 4 + 4 + 4 + 4 + 4 можна замінити виразом 4  5 або 20.

Два довільних числові вирази А і В, з’єднані між собою знаком рівності „=”, утворюють числову рівність (записується А = В). Числові вирази А і В називаються частинами числової рівності: А – лівою, В – правою.

З точки зору математичної логіки числова рівність є висловленням, яке істинне тоді і тільки тоді, коли значення лівої частини дорівнює значенню правої частини. Істинне висловлення, що визначається числовою рівністю, часто називають істинною (правильною) числовою рівністю. Над числовими рівностями як над висловленнями можна виконувати всі операції логіки висловлень, зокрема кон’юнкцію і диз’юнкцію.

Істинні числові рівності мають властивості, що базуються на властивостях дійсних чисел.

1. Якщо до обох частин числової рівності додати (відняти) один і той же числовий вираз, то знову одержимо числову рівність:

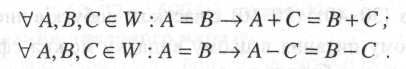
Відношення рівності числових виразів має рефлексивну властивість, тому для довільних числових виразів А і С

А + С = А + С (1)

За умовою А = В. Замінивши А на В у правій частині рівності (1), на підставі симетричної властивості відношення рівності одержуємо

А + С = В + С.

Наслідок 1. Якщо одна з частин числової рівності є алгебраїчною сумою, то будь-який її доданок можна з однієї частини перенести в другу частину, але при цьому його знак змінити на протилежний, зокрема

Наслідок 2. Якщо в обох частинах числової рівності є рівні доданки, то їх можна опустити, і знову одержимо числову рівність, зокрема

2. Числові рівності можна почленно додавати (віднімати), ізнову одержимо числову рівність, зокрема

Нехай А, В, С, і F – довільні числові вирази, при яких

за властивістю 1;

за транзитивністю відношення рівності

для числових виразів;

.

Аналогічно доводяться такі властивості числових рівностей.

3. Якщо обидві частини числової рівності помножити на один і той же числовий вираз, то знову одержимо числову рівність:

4. Якщо обидві частини числової рівності поділити на один і той же числовий вираз, значення якого відмінне від нуля, то знову одержимо числову рівність:

5. Числові рівності можна почленно перемножати, і знову одержимо числову рівність, зокрема

6. Обидві частини числової рівності можна почленно підносити до степеня з натуральним показником, і знову одержимо числову рівність:

7. Якщо числові вирази, відмінні від нуля, рівні між собою, то рівними будуть і обернені їм вирази:

3. Числові нерівності та їх властивості

З двох числових виразів більшим називається той, значення якого більше, і позначається знаком „ >”:

де а і b є відповідно значеннями виразів А і В. Відношення "більше" на множині числових виразів є відношенням строгого лінійного порядку, бо таким воно є для числових множин. Це дає можливість класи рівних між собою числових виразів строго лінійно впорядкувати.

Відношення "менше" (позначається "<") означається як обернене до відношення "більше", а тому воно також є відношенням строгого лінійного порядку.

Відношення "більше або дорівнює" (позначається ">") на множині числових виразів означається як об’єднання двох відношень "рівне" і "більше". Відношення ж "менше або дорівнює" (позначається " ") може бути означене або як об’єднання відношень "рівне" і "менше", або ж як відношення, обернене до відношення "більше або рівне". Останніх два відношення є відношеннями нестрогого лінійного порядку на множині числових виразів.

Два довільних числових вирази А і В, між якими поставлено один із знаків "<", ">", "<", ">", утворюють числову нерівність (записується А<В, А>В, А<В, А>В). Числові вирази А і В називаються частинами числової нерівності, А – лівою, В – правою.

Числова нерівність є також висловленням, яке істинне тоді і тільки тоді, коли значення лівої частини перебуває зі значенням правої частини в тому відношенні, що визначається знаком нерівності. Істинне висловлення, що задається числовою нерівністю, називається істинною числовою нерівністю.

До числових нерівностей, як і до числових рівностей, застосовуються операції логіки висловлень, зокрема кон’юнкція і диз’юнкція. Наприклад, для числових нерівностей 3 < 5 і 7 > 10 їх кон’юнкція має вигляд (3 < 5) л (7 > 10) записується

а диз’юнкція (3 < 5) л (7 > 10) записується

Логічне значення кон’юнкції – "0", а диз’юнкції – "1", бо складові висловлення мають різні логічні значення: "3 < 5" – "1", а "7 > 10 " – "0".

Дві або більше числові нерівності називаються нерівностями одного (однакового) смислу, якщо в усіх них ліві і праві частини перебувають в одному і тому ж відношенні порядку. Дві числові нерівності називаються нерівностями протилежного смислу, якщо відношення, в якому з перебувають ліва і права частина однієї з них, є оберненим до відношення порядку, що пов’язує ліву і праву частини другої нерівності.

Наприклад, числові нерівності А₁ > В₁, А₂ > В₂, А₃ > В₃ є нерівностями однакового смислу, а числові нерівності С  F і С  F є нерівностями протилежного смислу.

Істинні числові нерівності мають ряд властивостей, що базуються на їх означеннях та властивостях дійсних чисел:

1.

2. l)

2)

Доведемо І). Нехай А і В – довільні числові вирази, значеннями яких є числа а і b, відповідно такі, що

А >В  за означенням відношення "більше" для числових виразів;

а > b  за означенням відношення "більше" для дійсних чисел;

а – b > 0  за означенням відношення "більше" для числових виразів;

А – В > 0.

3. Якщо до обох частин числової нерівності додати (відняти) один і той же числовий вираз, то знову одержимо нерівність того самого смислу, що й задана, зокрема

1)

2)

Доведемо 1). Нехай А, В, С – довільні числові вирази, значення яких а, b, с відповідно такі, що

А > В  за властивістю 2;

А – В > 0  за означенням відношення "більше" для числових виразів;

а – b > 0  за властивістю нуля при додаванні дійсних чисел;

(а – b) + 0 > 0  за властивістю додавання протилежних чисел;

(а – b) + (с – с) > 0 => за властивістю додавання і віднімання дійсних чисел;

(а + с) – (b + с)>0  за монотонністю додавання дійсних чисел;

а + c > b + с  за означенням відношення "більше" для числових виразів;

А + С > В + С.

Наслідок 1. Якщо хоч одна з частин числової нерівності є алгебраїчною сумою числових виразів, то будь-який доданок можна перенести з однієї частини в другу, змінивши знак перед ним на протилежний, зокрема

Наслідок 2. Якщо в обох частинах числової нерівності є рівні доданки, то їх можна опустити, і одержимо нерівність того ж смислу, зокрема

4. Числові нерівності одного і того ж смислу можна почленно додавати, і знову одержимо нерівність того ж смислу, що й дані, зокрема

Нехай А, В, С, F – довільні числові вирази такі, що

(А > В)  (С > F)  за властивістю 3;

(А + С > В + С)  за транзитивністю відношення "більше"

(В + С > В + F)

А + С >В + F.

5. Числові нерівності протилежних смислів можна почленно віднімати, і одержимо нерівність того ж смислу, що й нерівність, від якої віднімають, зокрема

Нехай А, В, С, F – довільні числові вирази такі, що

(А > В)  (С < F) за властивістю 1;

(А > В)  (F > С)  за властивістю 4;

А + F > В + С  за наслідком 1;

A – C > B – F.

Розглядаючи наведені нижче властивості числових нерівностей слід звернути увагу на те, що знаки одержуваних нерівностей істотно залежать від того, на додатний чи від’ємний числові вирази множаться вихідні нерівності.

6. Якщо обидві частини числової нерівності помножити (поділити) на один і той же числовий вираз, значення якого додатне, то одержимо нерівність того ж смислу, що й дана, зокрема

7. Якщо обидві частини числової нерівності помножити (поділити) на один і той же числовий вираз, значення якого від’ємне, то одержимо нерівність протилежного смислу до даної, зокрема

Нехай А, В, С – довільні числові вирази, значеннями яких є дійсні числа а, Ь, с, відповідно такі, що

(А > В)  (С < 0)  за означенням відношень " > " і " < " для числових виразів;

(а > b)  (с < 0)  за властивістю множення дійсних чисел;

ас < be  за властивістю відношень ">" і "<" для числових виразів;

АС < ВС.

8. Числові нерівності одного і того ж смислу з додатними частинами можна почленно множити і одержимо нерівність того ж смислу, що й задані, зокрема

Нехай A, B, C, F – довільні додатні числові вирази, такі, що

(А > В)  (С > F)  за властивістю 6;

(АС > ВС)   за транзитивністю відношення "більше"

 (ВС > BF) для числових виразів;

AC > BF.

Наслідок 3. Обидві частини числової нерівності з додатними частинами можна підносити до степеня з натуральним показником і одержимо нерівність того ж смислу, що й задана, зокрема

9. Дві числові нерівності одного і того ж смислу з від’ємними частинами можна почленно перемножати і одержимо нерівність протилежного смислу до даних нерівностей, зокрема

10. Відношення порядку, що пов’язують два додатних (від’ємні) числові вирази і вирази, які є обернені до них, є оберненими між собою, зокрема