Черкаський державний технологічний університет

Кафедра радіотехніки

КОНТРОЛЬНЕ ЗАВДАННЯ

з дисципліни «Сигнали та процеси в радіотехніці»

для студентів спеціальності 6.050901 Радіотехніка

Білет № 57

1. Елементи загальної теорії радіотехнічних сигналів. Класифікація радіотехнічних сигналів. Сигнал і його математична модель.

2. Умова існування спектральної щільності сигнала. Властивості дійсної та уявної частин спектральної щільності. Спектральна щільність сигнала, зсунутого у часі.

3. Маємо імпульсний сигнал прямокутної форми тривалістю 5 мкс і амплітудою 15 В. Початок відліку часу співпадає з фронтом імпульса. Записати аналітичний вираз для цього сигналу.

, В

15

10

5

0 t, мкс

0 2,5 5 7,5 10

4. Амплітуда несучого ВЧ-коливання дорівнює В. Коефіцієнт модуляції М=0,65. Розглядається випадок однотональної модуляції. Визначити амплітуду верхньої бокової складової.

1. Одновимірні та багатовимірні сигнали.

2. Спектральна щільність похідної та інтеграла.

3. Обчислити енергію сигнала , що являє собою імпульс напруги; форма імпульса трикутна з висотою В і тривалістю мкс.

U

t

4. Амплітуда несучого ВЧ-коливання 4 В. Коефіцієнт модуляції 70%. Знайти максимальне і мінімальне значення однотонального АМ – сигнала.

1. Детерміновані та випадкові сигнали.

2. Спектральна щільність добутку сигналів.

3. Обчислити норму сигнала , що являє собою імпульс напруги; форма імпульса трикутна з висотою В і тривалістю мкс.

U

t

4. Амплітуда несучого ВЧ-коливання 4 В. Максимальне значення АМ-сигнала 5 В. Мінімальне значення АМ-сигнала 2 В. Визначити величини коефіцієнтів модуляції вгору і вниз.

1. Імпульсні сигнали.

2. Умова існування спектральної щільності сигнала. Спектральна щільність неінтегровних сигналів. Спектральна щільність постійного у часі сигнала.

3. Маємо радіоімпульс з прямокутною формою обвідної. Імпульс існує на інтервалі часу і описується функцією . Записати аналітичний вираз для норми радіоімпульса.

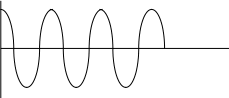S

U₀

t

0

4. Низькочастотний модулюючий сигнал має нижню частоту ( ) і верхню ( ). Визначити ширину спектру АМ-сигнала, якщо частота несучого коливання ( ).

1. Аналогові, дискретні та цифрові сигнали.

2. Умова існування спектральної щільності сигнала. Спектральна щільність неінтегровних сигналів. Спектральна щільність комплексного експоненційного сигнала.

3. Маємо радіоімпульс з прямокутною формою обвідної. Імпульс існує на інтервалі часу і описується функцією . Для випадку обчислити величину енергії радіоімпульса. В; мкс.

S

U₀

t

0

4. Однотональний ЧМ-сигнал має девіацію частоти кГц. У випадку індекса модуляції одержуємо рівність . Знайти частоту модуляції , при якій несуче коливання у спектрі сигнала буде відсутнє.

1. Динамічне представлення сигналів. Принцип динамічного представлення.

2. Умова існування спектральної щільності сигнала. Спектральна щільність неінтегровних сигналів. Спектральна щільність гармонічного сигнала. Спектральна щільність довільного періодичного сигнала.

3. Маємо радіоімпульс з прямокутною формою обвідної. Імпульс існує на інтервалі часу і описується функцією . Для випадку обчислити величину норми радіоімпульса. В; мкс.

S

U₀

t

0

4. Транзистор, який використовується в схемі модулятора, має злам характеристики в точці В. Амплітуда коливань несучої частоти на вході В, амплітуда модулюючого сигнала В, початкове зміщення В. Обчислити максимальне та мінімальне значення кута відсічки.

1. Функція включення.

2. Умова існування спектральної щільності сигнала. Спектральна щільність неінтегровних сигналів. Спектральна щільність функції включення.

3. Маємо експоненційний імпульс напруги (В):

.

Знайти, чому дорівнює норма цього сигнала.

4. Транзистор, який використовується в схемі модулятора, має злам характеристики в точці В. Амплітуда коливань несучої частоти на вході В, амплітуда модулюючого сигналу В, початкове зміщення В. Знайти коефіцієнт модуляції вихідного сигналу.

1. Динамічне представлення довільного сигнала за допомогою функцій включення.

2. Умова існування спектральної щільності сигнала. Спектральна щільність неінтегровних сигналів. Спектральна щільність радіоімпульсів

3. Маємо експоненційний імпульс напруги (В):

.

Знайти, чому дорівнює норма цього сигнала.

4. У схемі діодного детектора кОм, крутизна характеристики діода мА/В. Визначити коефіцієнт детектування.

1. Дельта-функція.

2. Умова існування спектральної щільності сигнала. Спектральна щільність неінтегровних сигналів. Спектральна щільність прямокутного відеоімпульса.

3. Маємо два зміщених у часі експоненційних імпульси напруги (В):

; .

Знайти скалярний добуток цих сигналів.

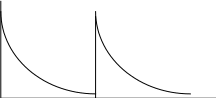U₁ U₂

t, мкс

0 2 4

4. У схемі амплітудного модулятора транзистор працює з мінімальним кутом відсічки рад. Обчислити, чому буде дорівнювати функція Берга при такому значенні кута відсічки.

1. Динамічне представлення сигналів за допомогою дельта-функцій.

2. Оптимальність розкладання сигнала по ортогональному базису.

3. Маємо два зміщених у часі експоненційних імпульси напруги (В):

; .

Скалярний добуток дорівнює В^2.с.

Знайти величину кута між цими сигналами згідно концепції сигнала як вектора у нескінченновимірному просторі.

U₁ U₂

t, мкс

0 2 4

4. У схемі амплітудного модулятора транзистор працює з максимальним кутом відсічки рад. Обчислити, чому буде дорівнювати функція Берга при такому значенні кута відсічки.

1. Геометричні методи в теорії сигналів. Лінійний простір сигналів.

2. Поняття комплексної частоти.