18. Составной код. Итеративные коды.

Итерационный код обладает теми же свойствами что и код Хэмминга, является линейным, в наиболее простом случае позволяет корректировать одиночные ошибки. Использование данного кода определяется записью проверочных символов в идее двумерной матрицы.

Простейшим из них является двумерный линейный итеративный код, п ри использовании которого кодовые слова записываются в виде таблицы. Основной является форма записи, при которой строки и столбцы содержат четное (нечетное) число единиц. Например, при кодировании информационного слова Х_k = 011101111 с помощью таблицы с четностью по строкам и столбцам получим избыточные символы Х_r = X_h, X_v = 0010011, как показано на рис. 3.3 (информационные символы выделены жирным шрифтом, а проверочные – курсивом).

Горизонтальные проверки

k₂

0 k1 1 1	0
1 0 1	0
1 1 1	1
0 0 1	1

Вертикальные проверки

Рис. 3.3. Схематичное представление (в виде таблицы) двумерного линейного итеративного кода

Кодовое слово имеет вид: X_n = 0111011110010011.

Порождающая матрица для двумерного линейного итеративного кода (4, 3, 4, 3) с d_min = 4, приведенного на рис. 3.3, будет иметь следующий вид:

(3.16)

Число проверочных символов определяется следующей зависимостью:

Местоположение ошибки находится на пересечении строки и столбца с нарушенной четностью.

Следовательно, двумерный линейный итеративный код (d_min=4) позволяет корректировать все одиночные ошибки с одновременным обнаружением двукратных.

19. Особенности использования перемежителей.

Перемежение – разнесение, разбрасывание бит в ином порядке, чем в исходном слове.

Глубина перемежения или min расстояние – это важнейшее характеристика перемежения.

а1 а2 а3 а4

а3 а1 а4 а2

Цель перемежения – разнесение групповых символов в разные части слов, чтобы на выходе можно было использовать более простые коды ошибок.

Благодаря перемежению на входе декодера ошибки равномерно распределяются во времени, в идеале образуя поток независимых ошибок

20. Циклические коды

Цель. Рассмотреть математический аппарат помехоустойчивого кодирования на основании циклических полиномов.

Пусть подлежит отправке информационное сообщение

.

Данному сообщению можно сопоставить полином, как показано ниже на рис 4.12:

1 0 1 0

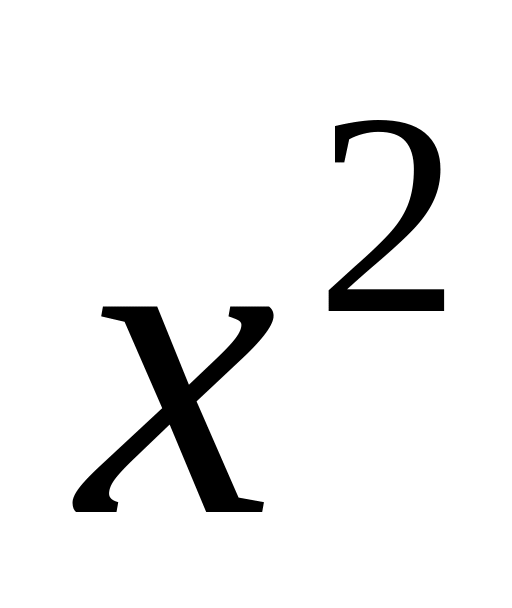
Рис. 4. 12.

Коэффициенты у полинома, полученного таким способом, равны 0 или 1 (члены полинома с нулевыми коэффициентами просто не выписываем). Далее такой полином будем называть циклическим. Особенностью циклических полиномов является то, что операции вычитания на поле таких полиномов нет – операция вычитания заменяется операцией сложения полиномов. Более того, операция сложения выполняется также специфически. Никаких переносов не существует. Если число слагаемых с одной и той же степенью k при x четное, то результатом будет 0; если нечетное – то результатом будет .

Пример.

,

,

.

Умножение выполняется обычным образом, но сохраняется введенное правило сложения.

Пример.

1. ,

,

.

2. ,

,

Определение. Циклический полином P называется первичным, если его нельзя представить как произведение , где и отличны от 1 и самого P.

Первичными полиномами, например, являются , , , и т.д.

Итак, прежде всего, определяются дополнительные разряды, присоединяемые к передаваемому информационному сообщению. Для выбора числа дополнительных разрядов будем использовать результат Боуза и Чоудхури, который состоит в следующем. Пусть n – число информационных разрядов. Пусть k – число дополнительных разрядов. Требуется выполнение следующих условий:

a) для некоторого целого m (любого подходящего);

b) , где – число обнаруживаемых ошибок.

Для получим:

,

.

Сложив эти неравенства и, полагая , получим:

Это соотношение в точности копирует (4.12) для кодов Хэмминга. Итак, в нашем случае возьмем . Значения дополнительных разрядов получают так. Умножают исходный полином на полином . В нашем случае и делят на первичный полином степени k (например, возьмем ). Остаток от деления и даст нам дополнительные разряды.

Итак, имеем:

1)

2)
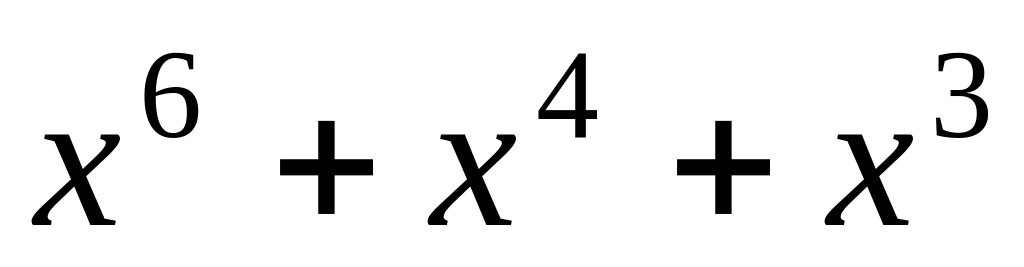
		– остаток

Еще раз напомним, что операция вычитания над полем циклических полиномов нет. Вычитание заменяется сложением, которое выполняется по сформулированным выше правилам.

Остаток можно записать так

(так как у нас число дополнительных разрядов ).

Этому полиному соответствует двоичный код 001.

Итак, мы должны передать число I = 1010. Для него мы определили дополнительные контрольные разряды 011. При этом нами использован первичный полином степени – . Отправляемое сообщение имеет такой вид:

1010’011

Теперь рассмотрим, как обнаруживаются и исправляются одиночные ошибки.

Допустим, был искажен второй разряд, и, следовательно, принято число

= 1110011.

Переведем его в полиномиальную форму:

.

Теперь надо разделить на первичный полином . Если деление произойдет нацело без остатка, то ошибки нет. В противном случае сразу фиксируется факт ошибки и дальнейшие действия направлены на исправление ошибки. В нашем случае деление дает

	– остаток

Остаток указывает на ошибку. Поступают так: циклически сдвигают принятую комбинацию на один разряд влево:

1 110011

= 1100111.

Полученное таким образом число снова делят на первичный полином. Если в остатке получается число, отличное от 1, то производят очередной циклический сдвиг влево и снова делят и т.д. до тех пор, пока, наконец, в остатке не получится ровно 1. В нашем случае второе деление дает:

	– остаток

Остаток не равен 1. Производим циклический сдвиг:

1 100111

= 1001111.

Выполняем очередное деление

1	– остаток

Мы получили в остатке 1. Это означает, что процесс делений и сдвигов прекращается. Для исправления ошибки нужно к последнему делимому добавить 1:

+1

Сложение выполняется по правилам циклических полиномов (без переносов). Теперь нужно получить двоичное представление этого полинома:

1001110.

Наконец, нужно выполнить обратный циклический сдвиг вправо столько раз, сколь раз до этого сдвигали число влево:

1 001110

0 100111

1010011

Мы получили восстановленное число. Циклические коды позволяют обнаруживать и исправлять многократные ошибки. Этот вопрос здесь не рассматривается, см. например [].