Федеральное агентство по образованию

Уральский государственный технический университет - УПИ

Анализ устойчивости и расчет переходного процесса дискретной системы

Домашнее задание и методические указания по дисциплине «Основы теории управления» для студентов направлений и специальностей подготовки

230100 - Информатика и вычислительная техника 230101 - Вычислительные машины, комплексы, системы и сети 230102 - Автоматизированные системы обработки информации и управления

Екатеринбург

УГТУ-УПИ

2007

УДК 62.50

Составители: Л.А. Ванеева, Е.Э. Страшинин, А.В. Цветков

АНАЛИЗ УСТОЙЧИВОСТИ И РАСЧЕТ ПЕРЕХОДНОГО ПРОЦЕССА ДИСКРЕТНОЙ СИСТЕМЫ: домашнее задание и методические указания по дисциплине «Основы теории управления» /сост. Л.А. Ванеева, Е.Э. Страшинин, А.В. Цветков. Екатеринбург: УГТУ-УПИ, 2007. 11с.

Приводится описание исходной дискретной системы, для которой проводится анализ устойчивости, рассчитывается корректирующее звено, обеспечивающее минимальное время переходного процесса. Проводится расчет временных характеристик скорректированной системы.

Приведены методические указания для выполнения всех пунктов домашнего задания.

Библиогр.: 7 назв. Рис. 4.

Подготовлено кафедрой «Автоматика и информационные технологии».

Ó Уральский государственный

технический университет  УПИ, 2007

Оглавление

ВВЕДЕНИЕ 4

1. ОПИСАНИЕ СИСТЕМЫ 4

2. ПОРЯДОК ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ 5

3. МЕТОДИЧЕСКИЕ УКАЗАНИЯ 6

БИБЛИОГРАФИЧЕСКИЙ СПИСОК 9

Введение

Изучение раздела «Цифровые системы управления» предусматривает выполнение одного домашнего задания, в котором студенты закрепляют знания по оценке устойчивости дискретной системы, проводят расчет корректирующего звена и переходного процесса исходной и скорректированной систем.

1. Описание системы

Рассматривается цифровая электромеханическая следящая система, функциональная схема которой (рис.1) соответствует целому классу систем, реализующих цифровое управление положением рабочих органов производственного оборудования.

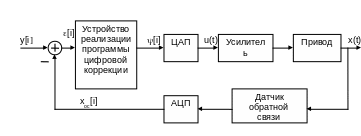
Рис.1. Функциональная схема системы

С помощью датчика обратной связи и аналого-цифрового пре­образователя (АЦП) контролируется координата x(t) в дискретные моменты времени - моменты съема t=iT₀, где i-целые неотрицательные числа (0,1, 2, 3,…), T₀ - период квантования сигналов по времени.

На выходе АЦП получается последовательность числовых кодов, которая описывается решетчатой функцией x_ос[i]=К_осx(iT₀), где K_ос-коэффициент обратной связи. При этом не учитывается квантование сигналов системы по уровню.

На входе системы в моменты съема задается управляющий сигнал y[i]. Рассогласование [i] = y[i] - x_ос[i] обрабатывается в реальном масштабе времени вычислительным устройством по программе цифрового корректирующего звена.

На выходе цифроаналогового преобразователя (ЦАП) образуется сигнал u(t), ступенчато изменяющийся при значениях t , незначительно запаздывающих относительно моментов съема iT₀ на время обработки сигналов в цифровой части системы. Этим запаздыванием можно пренебречь, так как рассматриваются достаточно большие постоянные времени привода.

Привод включает в себя электродвигатель, редуктор и механически связанные с ним другие массы, перемещаемые двигателем. Момент инерции, приведенный к валу двигателя, предполагается настолько значительным, что электромеханическая постоянная времени привода Т существенно превышает величины постоянных времени остальных элементов системы.

При указанных допущениях непрерывная часть системы определяется только усилителем и приводом и описывается передаточной функцией W(s)=K/s(Ts+1), где величина Т ,с, задается каждому студенту по номеру его варианта:

Т=0,5+0,1N.

Цифровая часть системы обеспечивает период квантования Т₀=1 с.

Статический передаточный коэффициент датчика обратной связи и АЦП принимается равным единице (К_ос=1). С учетом этого сигнал ошибки на выходе элемента сравнения определяется как [i]=y[i]-x[i].

Алгоритм пересчета величин [i] в значения [i] для цифрового корректирующего звена определяется указанными в задании требованиями к переходному процессу системы. Для ЦАП принимается единичный коэффициент преобразования, то есть u[i]=[i], где (i -1)T₀ t  iT₀. При t = iT₀ происходит ступенчатое (без разрыва) изменение u(t) от значения [ i – 1] до уровня [i].