2.5.1.5. Управление осями графиков.

При построении графика MATLAB автоматически находит максимальные и минимальные значения заданных выражений и выбирает соответствующий масштаб и обозначения осей. Для последующей настройки параметров осей используется функция axis. Так после создания графика можно многократно уточнять пределы осей, используя следующий формат записи функции:

Axis([xmin xmax ymin ymax]) . Здесь вектор аргументов содержит уточняемые минимальные и максимальные значения осей Х и Y.

Для управления внешним видом осей можно также использовать ключевые слова совместно с функцией axis:

axis square – создает Х и Y оси равной длины;

axis equal - задает равную длину интервала меток на осях;

axis auto – возвращает значение осей “по умолчанию”;

axis on – выводит обозначения осей и метки промежуточных значений;

axis off – выключает обозначения осей и метки промежуточных значений.

2.5.1.6. Подграфики.

Функция subplot позволяет выводить массив графиков на рабочем поле системы или при распечатке на одном листе бумаги. Формат записи:

subplot(m, n, p) , где m и n – соответственно числа строк и столбцов выводимой матрицы графиков; p - № текущего подграфика. Величина номера возрастает слева-направо и сверху-вниз.

2.5.1.7. График комплексного числа.

Если аргументом функции plot является комплексное число, то на графике оно представляется точкой с координатой по оси абсцисс равной величине действительной части числа и по оси Y – мнимой части числа. Если задать изменения значений действительной и мнимой частей числами, то график будет иметь вид:

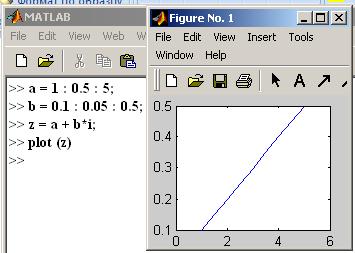
Если задать функцию plot с 2 аргументами, то система MATLAB игнорирует мнимую часть (или мнимые части, если оба аргумента комплексные). По оси Х будет размещаться значение аргумента, записанного первым (или его действительная часть, если этот аргумент – комплексное число). Соответственно значение второго аргумента записывается по оси Y. Содержания предупреждений системы в этих случаях видны на следующем рисунке (везде выводится точка):

8. Использование окна “Workspace” для задания типа и параметров графика [1, с. 113].

Если в командной строке заданы массивы, необходимые для построения графика, то можно вызвать функцию plot из диалогового окна “Workspace” вместо набора имени функции с клавиатуры. Окно можно вызвать с помощью меню (в версии 6:View – Workspace; в версии 7: Desktop -  Workspace), активизировать эти массивы щелчком мыши по именам массивов с удержанием <Ctrl> и выбрать тип графика из контекстного меню, открываемого щелчком правой кнопкой мыши (ПКМ) в окне Workspace:

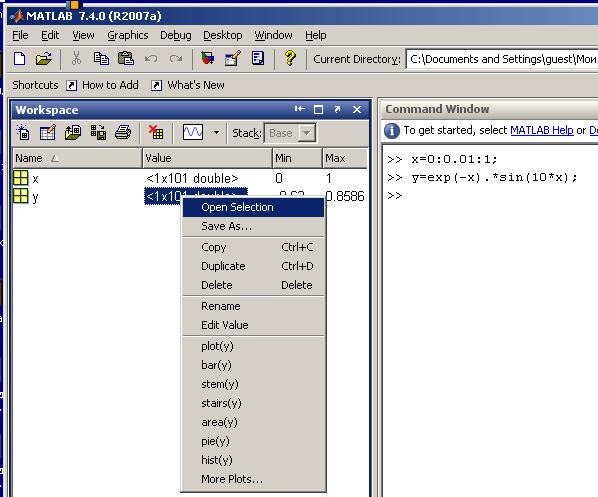
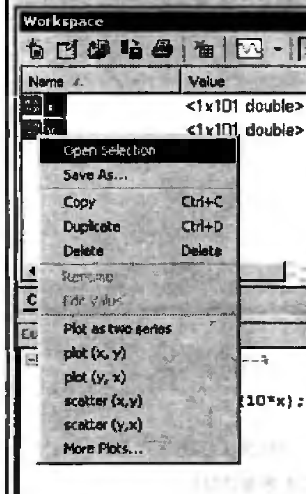
На рисунках видно различие содержания контекстного меню для случаев, когда выделена одна переменная или 2 переменных.

Нужную функцию можно также выбрать из раскрывающегося списка типов графиков на панели инструментов окна Workspace:

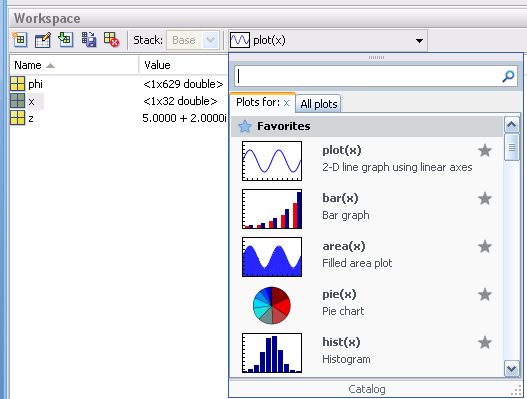
Эти действия приводят к автоматическому вызову, например, функции plot (или другой функции, возможной для выбранных аргументов), к появлению графика функции и к отображению в командном окне записи, связанной с низкоуровневой графикой:

plot(x,'DisplayName','x','YDataSource','x');figure(gcf) .

Функция в этом случае автоматически вызывается с использованием средств низкоуровневой графики, которые будут рассматриваться ниже. Достаточно подробно они описаны в [1, глава 9]. В окне Workspace для графического отображения, например, пары векторов х и у допустимо несколько способов; так выбор в меню или по элементам списка строки plot (х, у) приводит к созданию зависимости y(x); выбор plot (у, х) приводит к построению обратной зависимости х(у). Необходимо учитывать, что при попытке использовать векторы разной длины, система выдаст сообщение об ошибке.

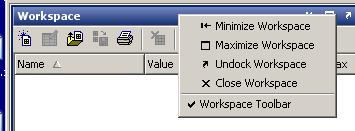
Если панель инструментов окна Workspace отсутствует, то ее можно отобразить при помощи контекстного меню окна. Для этого следует щелк-

нуть ПКМ по заголовку окна Workspace и в появившемся меню выбрать пункт Workspace Toolbar:

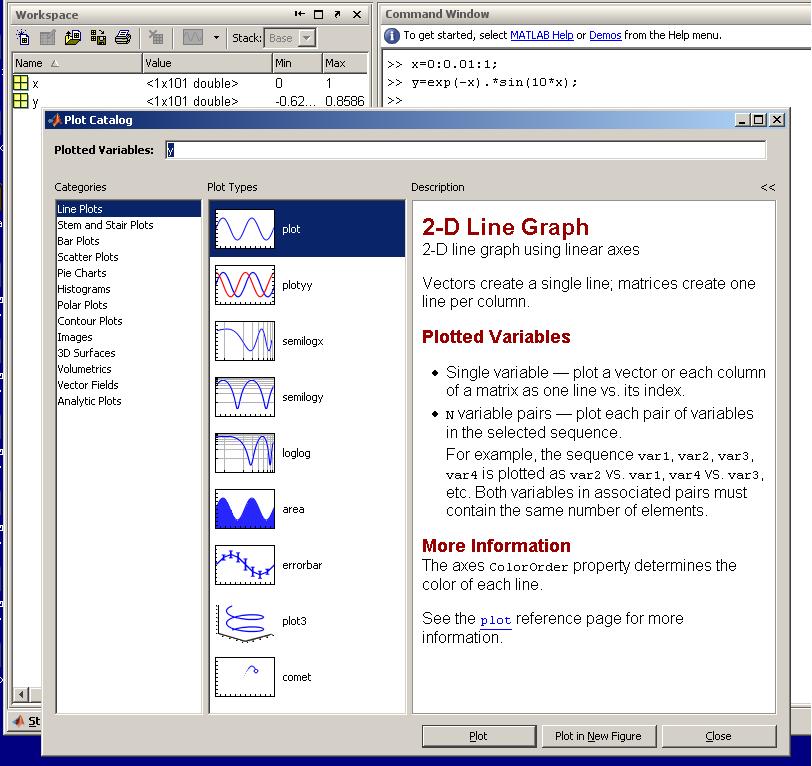
Список типов графиков окна Workspace содержит пункт More Plots (Другие графики), выбор которого приводит к открытию дополнительного окна для выбора типа графика: :

Окно позволяет выбрать категорию графика, типы графиков, относящиеся к каждой категории, и описание для отмеченного типа графика. Кнопки внизу окна дают возможность либо построить график в том же окне (“Plot”), либо в новом (“Plot in New Figure”), либо закрыть окно без построения (“Close”).

Переменные можно задавать непосредственно в окне Workspace. На панели инструментов этого окна есть пиктограмма “New variable”; использование этой пиктограммы и запись имени новой переменной иллюстрируются следующими рисунками:

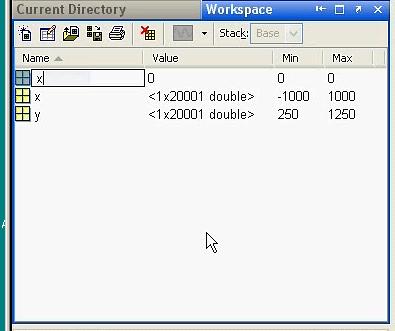
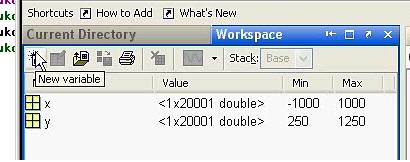
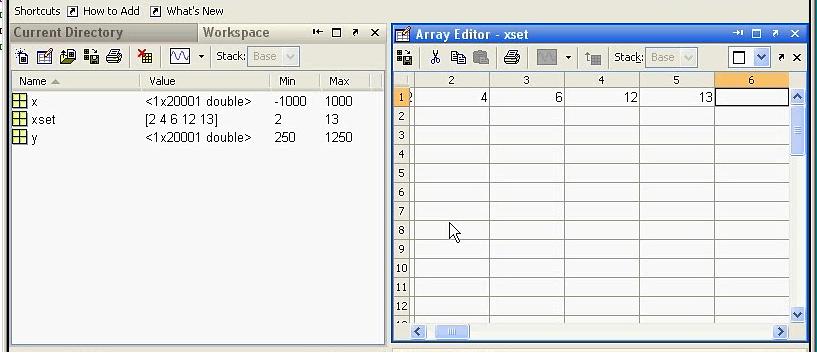
Если переменная является массивом, то двойной щелчок (2ЛКМ) по имени переменной в окне Workspace вызывает редактор массива, в котором удобно и наглядно можно присваивать значения элементов массива:

Литература.

1. Ануфриев И. Е., Смирнов А. Б., Смирнова Е. Н. MATLAB 7. Наиболее полное руководство.- СПб.: БХВ-Петербург, 2005. - 1104 с: ил.

Matlab7NaiboleePolnoeRukovodstvo.djvu, главы 3 и 4.

2. Иллюстрированный самоучитель по MatLab 6 (23 урока). Урок 6.

http://www.radiomaster.ru/cad/matlab/glava6/index1.php

3. В.Г.Потемкин. Система инженерных и научных расчетов Matlab 5.x. Том 2. –М.: Диалог-МИФИ, 1999, 304 с. (Глава 10).

http://www.exponenta.ru/SOFT/MATLAB/potemkin/book2/chapter10/contens.asp

Оглавление

2. MATLAB. 1

2.5.1.2. Графики в логарифмическом и полулогарифмическом 2

масштабах [3]. 2

2.5.1.3. График в полярных координатах [3]. 3

2.5.1.4. Оформление графиков [1, с.135] 3

2.5.1.5. Управление осями графиков. 5

2.5.1.6. Подграфики. 5

2.5.1.7. График комплексного числа. 5

2.5.1.8. Использование окна “Workspace” для задания типа и параметров графика [1, с. 113]. 6