2.2.5. Форматы вывода результата вычислений.

Формат числа определяет вид результата вычислений в командном окне. По умолчанию используется формат short (укороченный), при котором на экране отображаются только четыре цифры после десятичной точки. Это сделано для того, чтобы не перегружать подробностями командное окно. Формат вывода может быть изменен с помощью диалогового окна Preferences (раздел меню File - строка Preferences… (Предпочтения)):

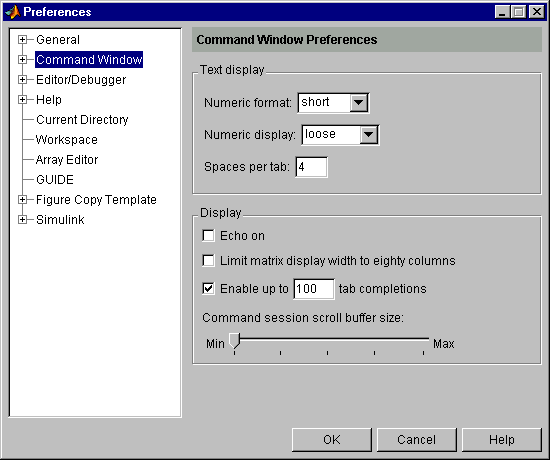
Для установки формата вывода следует убедиться, что в списке левой панели выбран пункт Command Window. Задание формата производится из раскрывающегося списка Numeric format группы полей Text display. На рисунке выбран формат “short”:

>> 200/3

ans =

66.6667

Этот формат вывода сохранится для последующих вычислений, пока не будет установлен другой формат. В MATLAB возможна ситуация, когда при отображении слишком большого или малого числа результат не укладывается в формат short. Так, например, при вычислении 100000/3 и 1/3000 результаты выводятся в экспоненциальной форме:

>> 100000/3

ans =

3.3333e+004

>> 1/3000

ans =

3.3333e-004

Если требуется получить результат вычислений более точно, то в раскрывающемся списке диалогового окна Preferences следует выбрать формат long. При этом результат будет отображаться в длинном формате с плавающей точкой long c 15 цифрами после десятичной точки. Форматы short e и long e предназначены для вывода результата в экспоненциальной форме соответственно с 4 и 15 цифрами мантиссы после десятичной точки. Информацию о форматах можно получить, набрав в командной строке команду doc format.

Задать формат вывода можно непосредственно из командной строки при помощи команды format. Например:

>> format long e

>> 1.33/5.13

ans =

2.592592592592593e-001

>> format long g

>> ans

ans =

0.259259259259259

>> format rat

>> 0.03333333

ans =

1/30

Формат с буквой g не выводит в показателе степени нули при научной форме записи числа; используется с – long и short (так, например, вместо 1.3333е+000 будет выводиться 1.3333). Формат rat устанавливает форму вывода, при которой вещественные числа приближённо представляются отношением двух небольших целых чисел.

Для того, чтобы выделить результат, MATLAB выводит его через строку после вычисляемого выражения. Иногда требуется разместить больше строк на экране. Для этого в диалоговом окне Preferences следует выбрать compact из раскрывающегося списка Numeric display. Добавление пустых строк обеспечивается выбором строки loose (широкий, свободный) из списка Numeric display.

Применение команды format без параметров восстанавливает используемое по умолчанию состояние format short.

Все промежуточные вычисления MATLAB производит с двойной точностью, независимо от того, какой формат вывода установлен.

2.2.6. Комплексные числа и комплексные функции.

Комплексные числа в системе MATLAB записываются в следующем виде:

3+2i; 7-4j; -3.8952+1.23e-5i; 5+i*7.

По умолчанию они имеют тип double. Для записи комплексного числа требуется в 2 раза больше памяти, чем для записи вещественного числа, так как по 8 байт памяти отводится для действительной Re z и мнимой Im z частей комплексного числа z. При вводе комплексных чисел системные переменные (мнимая единица ) i или j могут быть записаны до или после мнимой части. При записи перед Im z ставится знак умножения * после этих системных переменных. При записи мнимой единицы после Im z ставить знак умножения необязательно. Например, следующие записи эквивалентны:

1+i*2 ~ 1+j*2 ~ 1+2*i ~ 1+2*j ~ 1+2i ~ 1+2j (записи 1+i2 или 1+j2 не допустимы) . Возможна запись 1+i, которая не разрешалась, например, в MathCAD.

Если коэффициентом при мнимой единице является не число, а переменная, то простановка знака умножения обязательна, т.е. должна быть следующая запись: x+y*i. Если системным переменным i или j присвоить значение отличное от , то в текущем сеансе работы они перестанут выполнять функцию мнимой единицы.

Если в командную строку ввести i, получим

>> i

ans =

0 + 1.0000i

Тот же результат получим при вводе буквы j:

>> j

ans =

0 + 1.0000i

Кроме того, комплексное число можно представить в другом формате:

>> format long

>> 4-9j

ans =

4.00000000000000 - 9.00000000000000i

При выводе мнимая единица всегда обозначается буквой i и выводится после мнимой части.

Два комплексных числа считаются равными, если равны отдельно их действительные и мнимые части. Алгебраические действия над комплексными числами выполняются по следующим формулам (это не matlab-запись):

z₁ ± z₂=(x₁+iy₁) ± (x₂+iy₂)=(x₁ ± x₂)+i(y₁ ± y₂);

z₁ z₂=(x₁+iy₁)(x₂+iy₂)=(x₁x₂ - y₁y₂)+i(x₁y₂ +x₂y₁);

= ; здесь стрелка над именем переменной означает комплексно-сопряженное число.

Примеры:

>> 1+2i+3-4j

ans =

4.0000 - 2.0000i

>> (1+2i)*(3-4j)

ans =

11.0000 + 2.0000i

>> (1+2i)/(3-4j)

ans =

-0.2000 + 0.4000i

>> z=(3+2i)^3

z =

-9.0000 +46.0000i

Функции real и imag выделяют вещественную и мнимую части комплексного значения:

>> real(z)

ans =

-9

>> imag(z)

ans =

46

Функция complex формирует комплексное число по паре вещественных чисел:

>> z=complex(3,-4)

z =

3.0000 - 4.0000i

Функция conj возвращает комплексно–сопряженное число:

>> conj(z)

ans =

3.0000 + 4.0000i

Такой же результат получится, если поставить апостроф после мнимой части комплексного числа или после имени комплексной переменной:

>> z=1+2*i'

z =

1.0000 - 2.0000i

>> z'

ans =

1.0000 + 2.0000i

Возникающий в процессе вычислений с вещественными переменными комплексный результат не является ошибкой. Вычислить , оставаясь в рамках только вещественных чисел, нельзя. MATLAB автоматически перейдет к комплексным вычислениям и в итоге возвратит результат, равный i:

>> sqrt(-1)

ans =

0 + 1.0000i

В математике используют и другие формы представления комплексных чисел:

z= x+iy = ρe^i = ρ(cos φ+isin φ); здесь записи сделаны так, как это принято в математике, и не являются matlab-выражениями.

Здесь ρ=│z│= 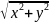– модуль комплексного числа, φ – фаза, или главное значение его аргумента (величина угла измеряется в радианах), причем tg φ= .

Значения этих параметров можно определить с помощью стандартных matlab-функций ρ=abs(z) и φ= angle(z).

Основные элементарные функции комплексного переменного (формулы “математические”, а не matlab-выражения):

показательная функция e^iz;

тригонометрические функции

cos z = 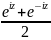sin z = ;

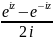гиперболические функции

ch z = 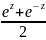, sh z = ;

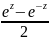главное значение логарифма

ln z = ln │z│+iarg z;

главные значения обобщенных показательной и степенной функций

a^z = e^{zln a} и z^= e^{ln z},

z, α, a – любые комплексные числа, a≠0.

Примеры matlab-записей, приведенных выше формул из математики:

>> exp(1+i)

ans =

1.4687 + 2.2874i

>> sin(1+j)

ans =

1.2985 + 0.6350i

>> i^i

ans =

0.2079

>> isreal(i^i)

ans =

1

>> (2+i)^(1-3i)

ans =

-3.3307 – 8.3459i

>> log(-1)

ans =

0+ 3.1416i

Литература.

1. В.Г.Потемкин "Введение в Matlab". Глава 1. http://www.nsu.ru/matlab/MatLab_RU/ml/book1/index.asp.htm

2. Автор не известен. Лекции по Маtlab 6.x . Высший Государственный Колледж Связи. Республика Беларусь. http://vgks.moy.su/load/3-1-0-29 (файл 29_Matlab.rar; глава 1.)

3. Иллюстрированный самоучитель по Matlab. Уроки 2,5.

http://www.radiomaster.ru/cad/matlab/index.php

Оглавление

2. MATLAB. 1

2.1. Назначение и особенности MATLAB. 1

2.2. Среда и интерфейс. 2

2.2.1. Операционная (рабочая) среда системы. 2

2.2.1.1. Окно рабочей среды MATLAB [2, глава 1,с.3]. 2

2.2.1.2. Режимы работы. Ввод с клавиатуры. 3

2.2.1.3.Зоны просмотра и редактирования. 5

2.2.1.4.Рабочее пространство. Ввод выражений. 5

2.2.2.Арифметические выражения. 8

2.2.3. Переменные. 9

2.2.4. Вещественные числа. 10

2.2.5. Форматы вывода результата вычислений. 11

2.2.6. Комплексные числа и комплексные функции. 12