7.2 Алгоритм обхода "снизу-вверх".

шаг 1. выбрать последовательно слева-направо вершины-стоки, соответствующие символам цепочки и найти вершину-исток на дереве;

шаг 2. если вершина-исток представляет начальный символ, то конец, иначе перейти к шагу 1.

Пример 27. Написать правильную цепочку и найти систему составляющих для синтаксического дерева, представленного на рис.6.

По правилам алгоритма "снизу-вверх" имеем правильную цепочку терминальных и нетерминальных символов:

c1Ca1DAbEc2Ga2HFBJ .

В цепочке также выделяются составляющие, но на первом месте каждой составляющей указывается ее значение, а на втором - имя: c1C; a1D; bE; c2G; a2H; c1Ca1DA; c2Ga2HF; bEc2Ga2HFB.

Хвостом каждой цепочки является синтаксическая переменная, что определяет условия использования правосторонней грамматики.

Система составляющих имеет вид:

на уровне членов предложения:

CJ = { (A,5);(F,12);(B,13)};

на уровне слов:

CJ = {(C,2);(D,4);(E,7);(G,9);(H,11)}.

Составляющие (C,2) и (D,4) вложены в составляющую (A,5), составляющие (G,9) и (H,11) вложены в (F,12), cоставляющие (E,7) и (F,12) вложены в (B,13).

Пример 28. Написать правильную последовательность символов и найти систему составляющих для синтаксического дерева, представленного на рис.7.

Совершая обход дерева "снизу-вверх", получим следующую цепочку:

a1a2A2A1c1iA3C1b1C2B4a3B3a4B2B1c2J.

Основными составляющими в написании программы являются

<заголовок программы> - a1a2A2c1A1 ;

";' - c1 ;

<блок > - iA3C1b1C2B4a3B3a4B2B1 ;

"." - c2 .

Система составляющих для этой цепочки может быть записана так:

CJ = { (A1,4); (c1,5); (B1,16); (c2,17) }.

В каждую из составляющих вложены другие составляющие, имеющие меньшую длину. Так, например, составляющие A2 и A3 вложены в A1, составляющие C1 и С2 - в B4, составляющая B4 - в B3,составляющая B3 - в B2, а составляющая B2 - в B1.

Пример 29. Написать правильную последовательность символов и найти систему составляющих для синтаксического дерева, представленного на рис. 8.

Используя правила алгоритма "снизу-вверх", правильная цепочка символов имеет вид:

iA3C1C4xD2iA3C1C4C3+D1iA3C1C4xD2iA3C1C4C3C2 .

Если принять основными составляющими цепочки нетерминальные символы С1 иС3 , то систему составляющих можно записать так:

СС2 = { (C1,3);(C1,9);(C1,16);(C1,22);(C3,11);(C3,24) }.

Составляющая С1 есть хвост подцепочки iA3C1.

8. Двоичное дерево

Особое место в анализе цепочек формального языка занимает двоичное дерево, в состав которого входят корень и два непересекающихся двоичных поддерева, называемых левым и правым поддеревьями данного корня. В отличие от дерева разбора из корня и каждого узла дерева исходит не более двух дуг. Такое дерево оказывается более удобным для применения системы составляющих в анализе синтаксических конструкций цепочек. На рис.13 показано двоичное дерево и его два поддерева: левое поддерево, когда правое - пусто и правое поддерево, когда левое - пусто.

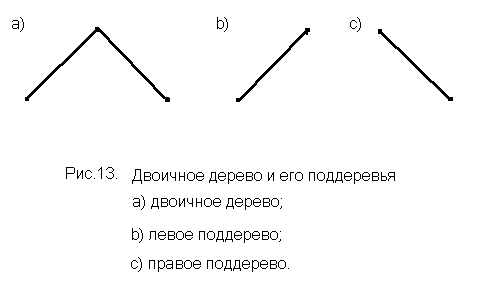
Для перехода от дерева разбора к его двоичному эквиваленту следует воспользоваться следующими правилами:

правило формирования левого поддерева: если вершина "K" является самым левым потомком вершины "J" в дереве разбора, то эта вершина формирует вершину-сток левого поддерева двоичного дерева и является левым потомком вершины "J" двоичного дерева; вершина-исток левого поддерева есть образ символа, находящегося в левой части правила грамматики, а вершина-сток - образ первого символа правой части правила грамматики;

правило формирования правого поддерева: если вершина "L" является старшим среди оставшихся (после удаления вершины "K" для формирования левого поддерева) братьев - потомков вершины "J" в дереве разбора, то эта вершина формирует вершину-сток правого поддерева двоичного дерева и является правым потомком старшего брата - вершины "K" ; все последующие братья - потомки вершины "J" в дереве разбора являются правыми потомками братьев по старшинству и формируют правые поддеревья двоичного дерева; вершина-исток правого поддерева есть образ предшествующего левого символа в правой части правила, а вершина-сток - образ следующего справа символа в правой части правила

Пусть дано правило J ::=KLM,

где J, K,L,M,  VN.

На рис.14а) представлен граф двоичного дерева. В составе этого дерева - одно левое поддерево, соединяющее вершины J и K и два правых, соединяющих вершины K и L , L и M.

Пусть дано множество правил КС-грамматики:

J ::= KLM, K ::= k и L ::= Pm,

где k,m  V_T,

J,K,L,M,P  V_N .

На рис. 14b) представлен граф двоичного дерева. В составе этого дерева три левых поддерева, соединяющих вершины J и K, K и k , L и P и три правых поддерева,соединяющих вершины K и L, L и M , Р и m.

Рассмотрим двоичные деревья для синтаксических деревьев и деревьев разбора, представленных в примерах 20, 21, 22 и 23.

Пример 30. Для синтаксического дерева, представленного на рис. 6, сформировать двоичное дерево.

На рис.15 представлен двоичный эквивалент дерева разбора в соответствии с правилами грамматики, заданными в примере 20.

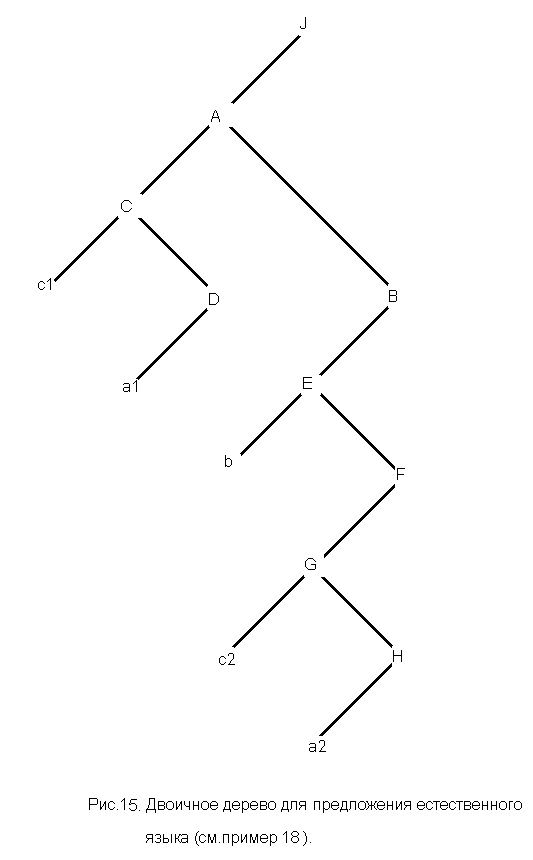
Пример 31. Для дерева разбора синтаксической переменной <программа> языка программирования Паскаль, представленного в примере 21 (рис. 7), сформировать двоичное дерево.

На рис.16 представлен двоичный эквивалент дерева разбора в соответствии с правилами грамматики, заданными в 2 (пример 1).

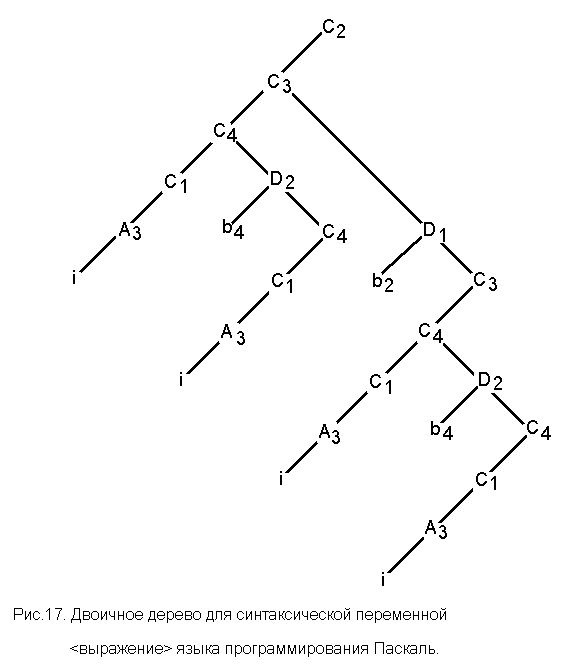
Пример 32. Для дерева разбора синтаксической переменной <выражение> языка программирования Паскаль, представленного в примере 22 (рис. 8), сформировать двоичное дерево.

На рис.17 представлен двоичный эквивалент дерева разбора в соответствии с правилами грамматики, заданными в 2 (пример 1).

Пример 33. Для синтаксических деревьев арифметических выражений:

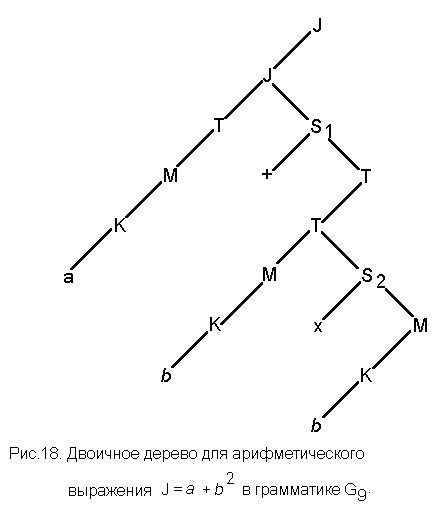
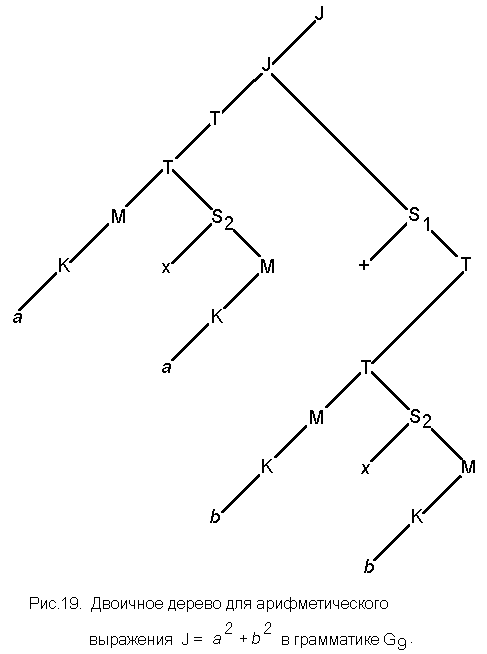
a) J = a +b², b) J = a² + b²,

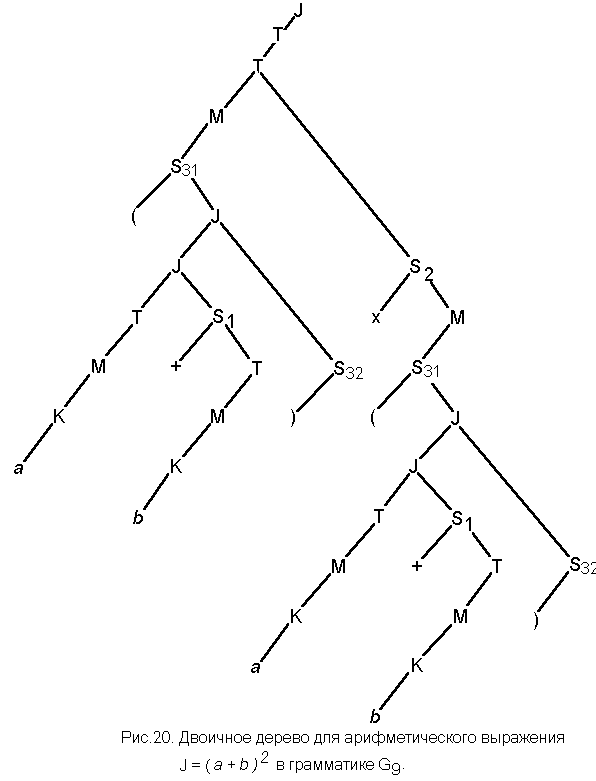
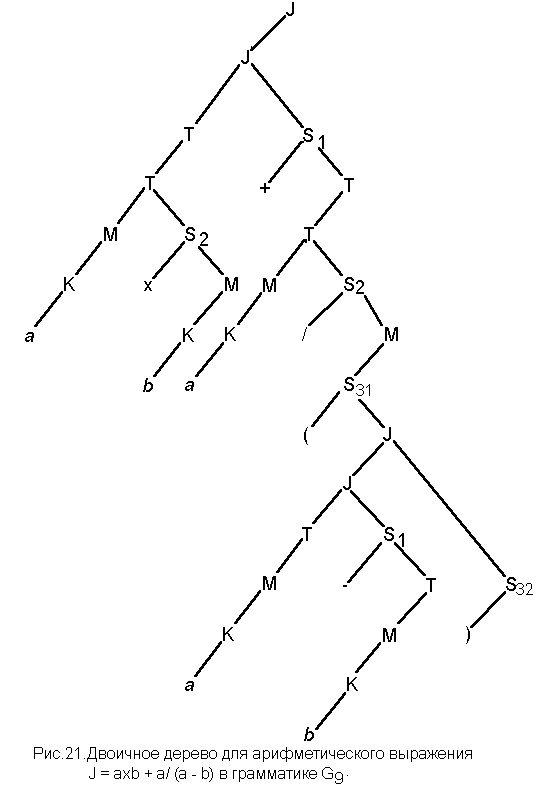
c) J = ( a + b )² d)J = a x b + a( a - b )

в грамматике G9, рассмотренных в примере 23 (рис. 9,10,11,12), сформировать двоичные деревья.

На рис.18, 19, 20 и 21 представлены двоичные эквиваленты синтаксических деревьев по правилам грамматики, заданными в 3 (пример 14).