15.Геометрические уравнения. Погонные силовые факторы. Разрешающие уравнения в перемещениях.
-
постоянная по толщине пластины.
- поворот вокруг оси у.
- поворот вокруг оси х.
Геометрические уравнения.
Физические уравнения (получаются на основе закона Гука).
Определим
:
Аналогично
Определим крутящий момент:
С- корректирующий коэффициент(5/6….8/9).
Уравнения равновесия.
Выделяется малый элемент и к нему прикладываются силовые факторы.
Разрешающие уравнения.
В
результате упрощения получим:
Элементы теории поверхностей
1.Расчетная схема оболочки. Основные определения. Срединная поверхность. Основные гипотезы классической теории оболочек.
Оболочка – тонкое тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми (толщина оболочки) много меньше его других размеров.
Поверхность, равноудалённая от наружной и внутренней поверхностей оболочки, называется срединной поверхностью.
Основные гипотезы классической теории оболочек (гипотезы Кирхгофа-Лява):
Гипотеза прямых нормалей
Материальный элемент нормальный к срединной поверхности до деформации, после деформации остается прямым, нормальным деформированным к срединной поверхности и не изменяет своей длины.
Гипотеза ненадавливания.
Нормальными напряжениями в слоях эквидистантных к срединной поверхности можно пренебречь по сравнению с другими компонентами тензора напряжения
2.Координатный и векторный способ задания поверхности.
Координатный способ:
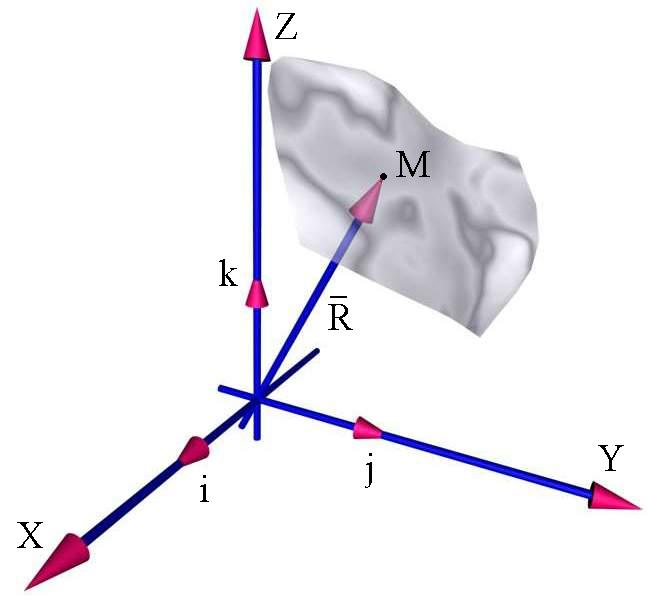
Векторный способ:
Примеры:
Цилиндр:
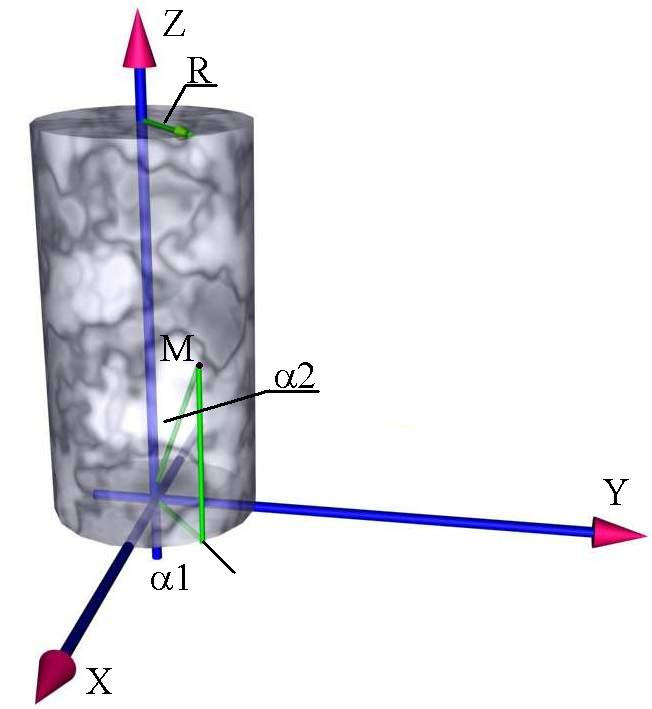
Сфера.
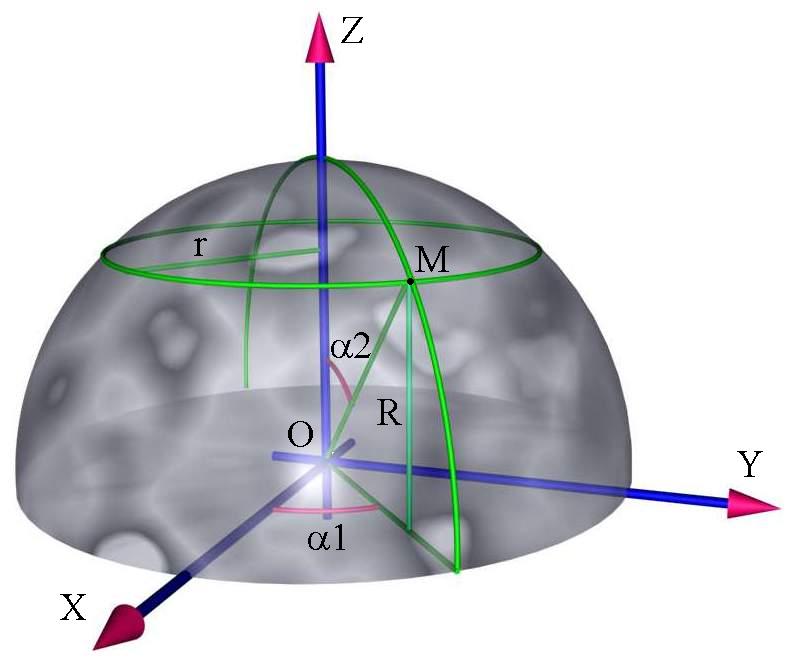(географическая
система координат)
3.Материальные координаты. Семейства координатных линий на поверхности оболочки
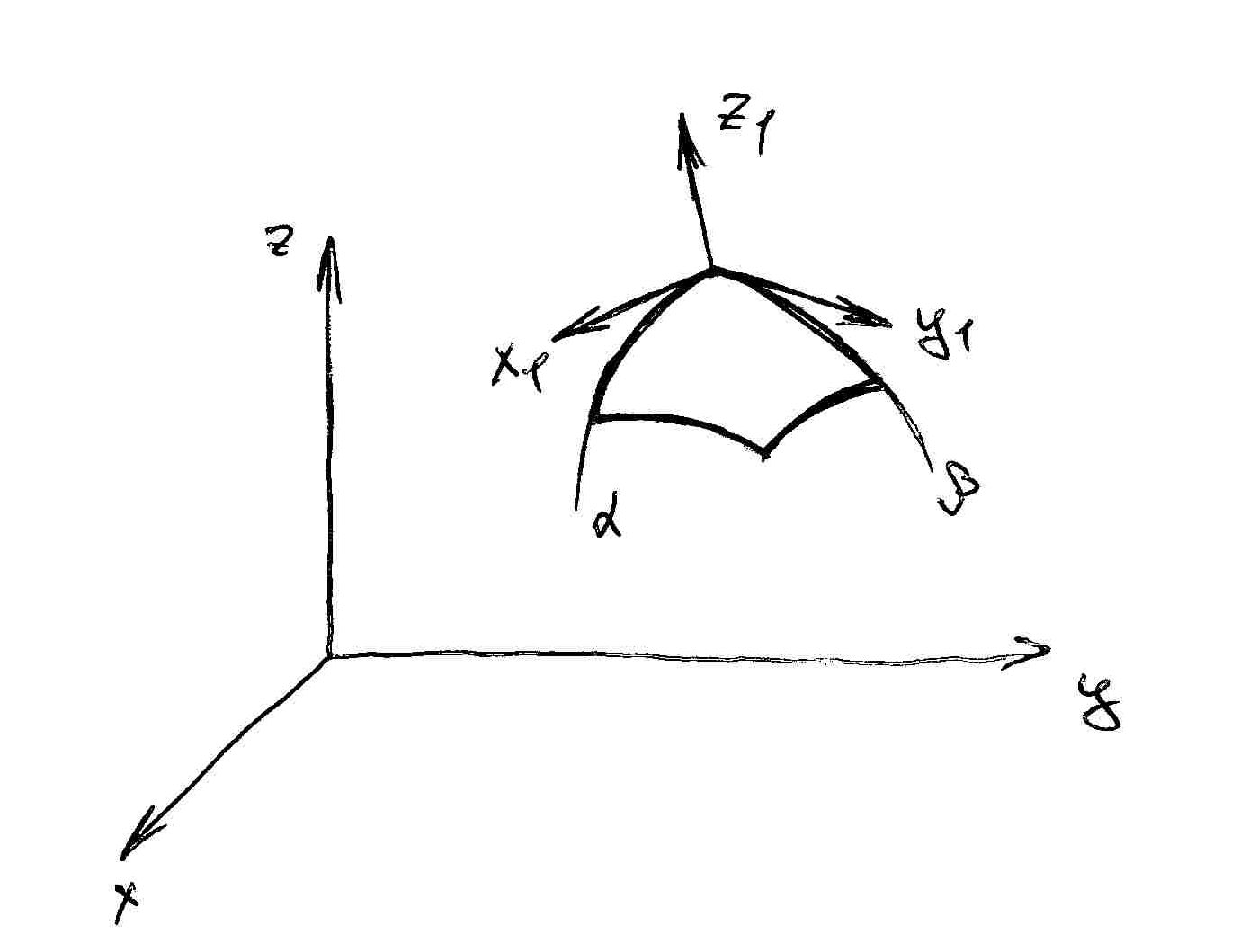
- линии главных кривизн оболочки
Касательно к линиям
проведены
оси
,
которые вместе с направленной вдоль
внешней нормали осью
образуют правый трехгранник
В итоге
- материальные координаты
Надо уточнить про координаты у Дмитриева!!!!!!!
Семейства координатных линий на поверхности оболочки:
- координатные линии
- координатные линии
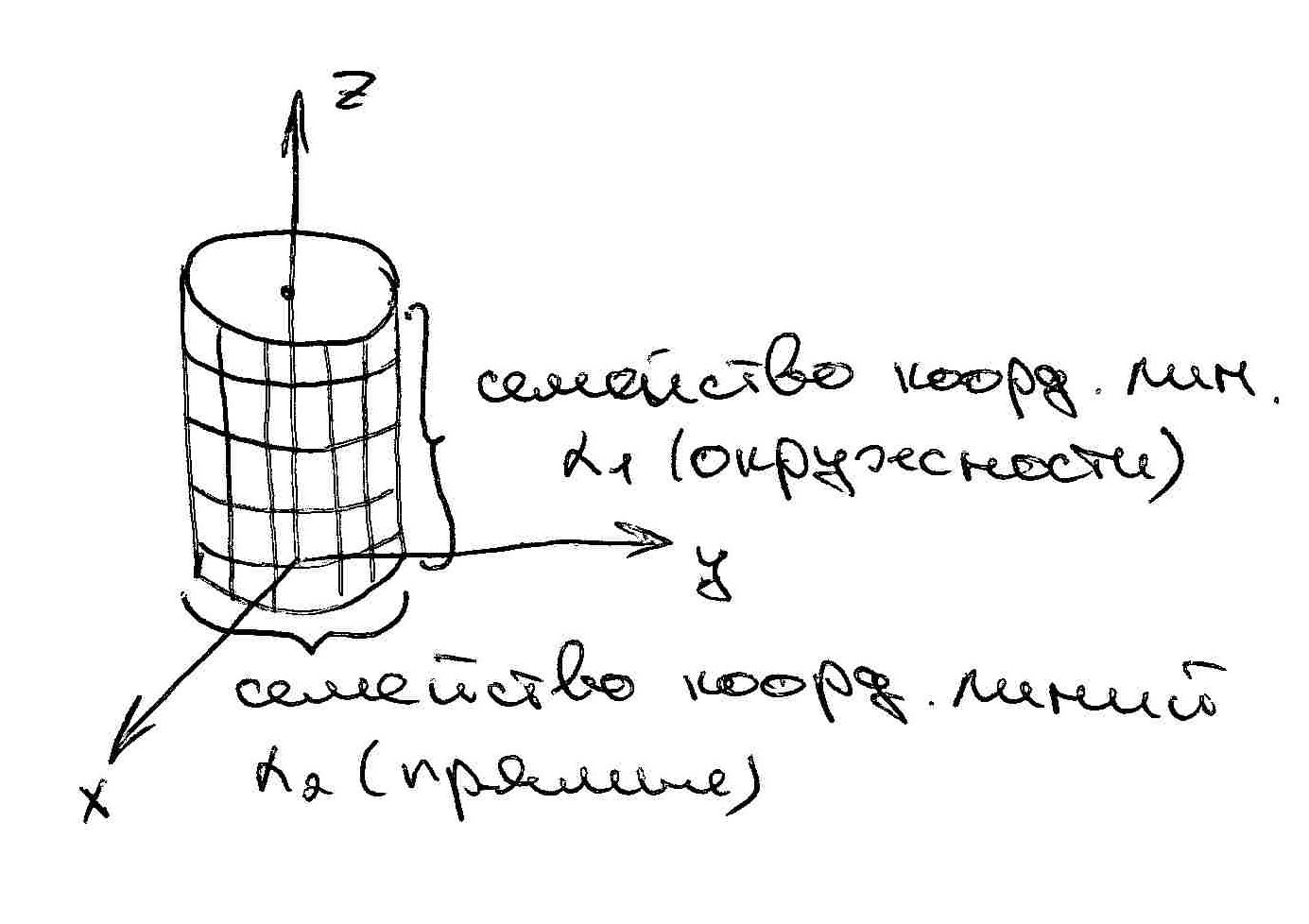
Координатные линии являются материальными (Лагранжевими)
4.Локальный координатный базис. Единичные векторы базиса. Параметры Ламе.
Единичные векторы локального координатного
базиса:
.
направлены по касательным к координатным
линиям
,
направлен по нормали к поверхности, так
что векторы
образуют правую тройку.
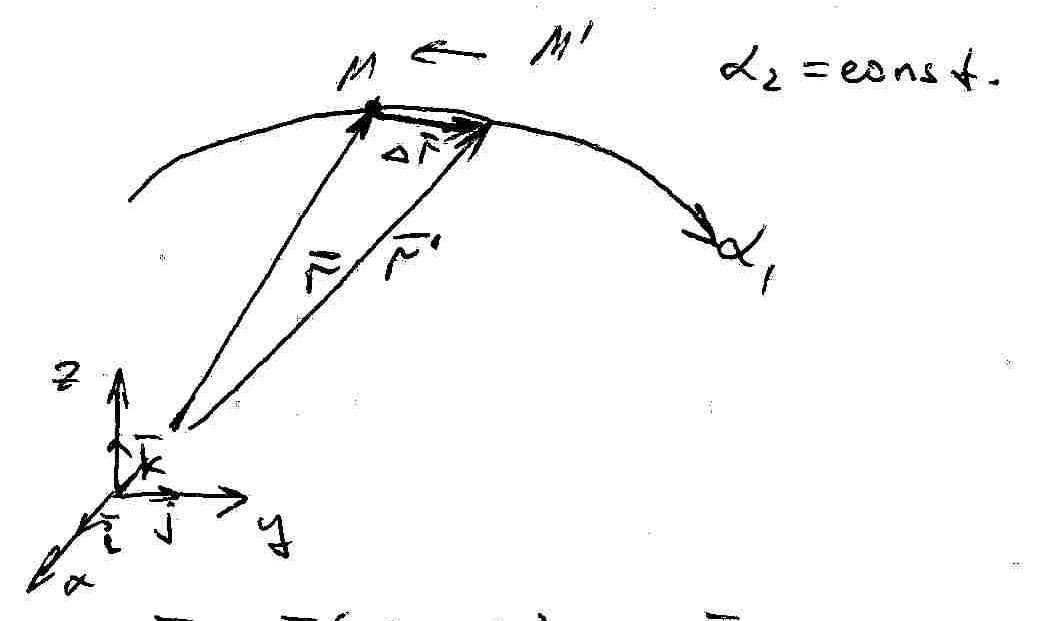
Касательная получается при стремлении М` к М
- направлен по касательной к координатной
линии
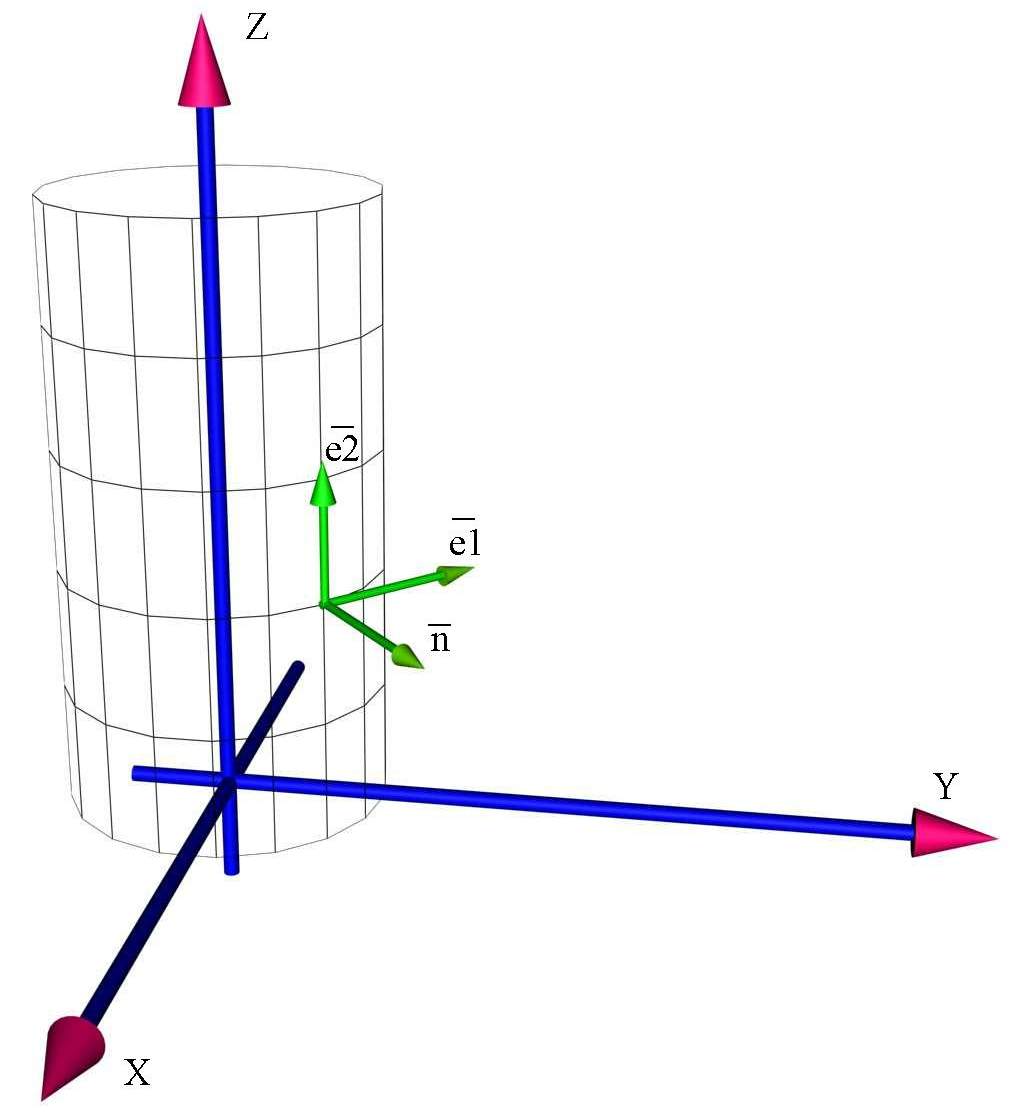
- параметры Ламе
5.Первая квадратичная форма. Определение длин дуг координатных линий, геометрический смысл параметров Ламе.
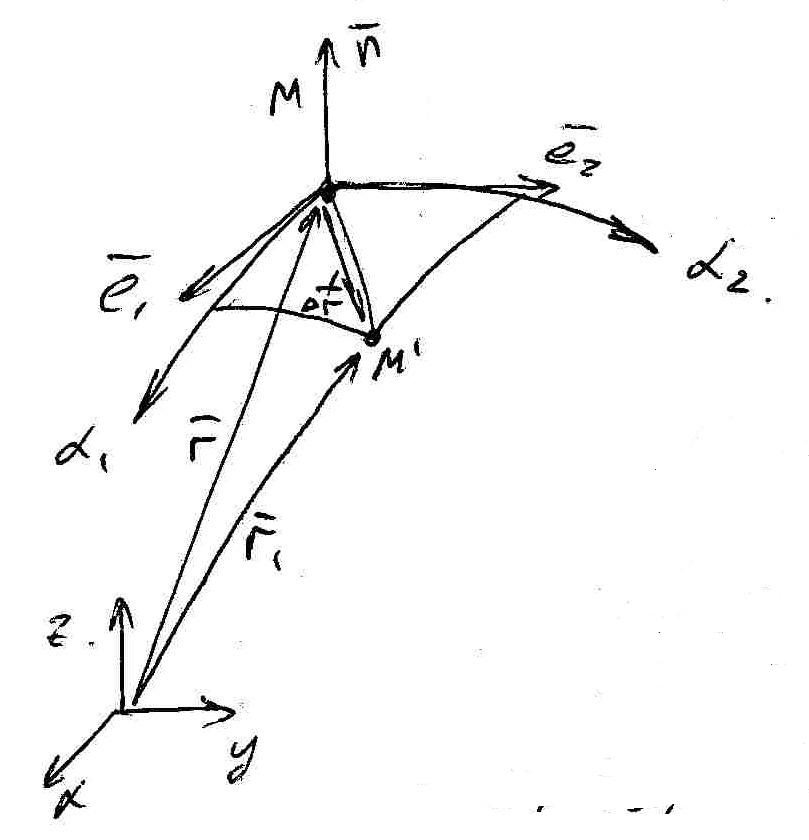
Она определяет расстояние между двумя точками, лежащими на поверхности.
- 1-я квадратичная форма(ПФК), где
- коэффициенты ПФК
В ортогональной системе координат
т.к.
Геометрический смысл параметров Ламе:
Приращение дуги координатной линии
Параметры Ламе связывают между собой приращение длины дуги координатной линии с приращением координаты.
6.Определение углов между единичными векторами. Ортогональные координаты. Первая квадратичная форма в ортогональных координатах.
- 1-я квадратичная форма (ПФК), где
- коэффициенты ПФК
- угол между
единичными векторами
Ортогональная система координат:
В ортогональной системе координат т.к.
7. Определение кривизны пространственной кривой.
Вторая квадратичная форма.
Она связана с кривизной поверхности.
Кривизна пространственной кривой.
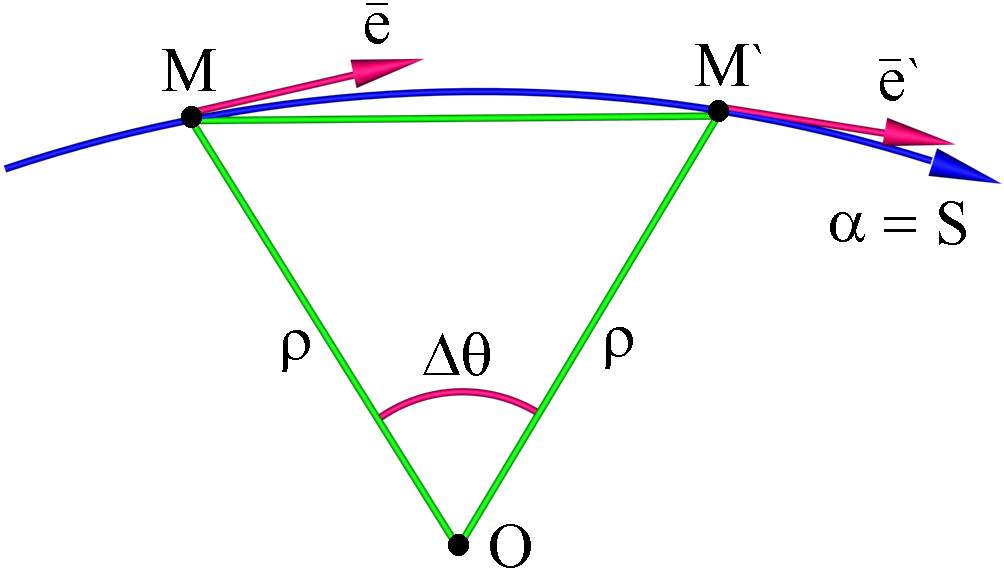
Длина дуги MM` - S
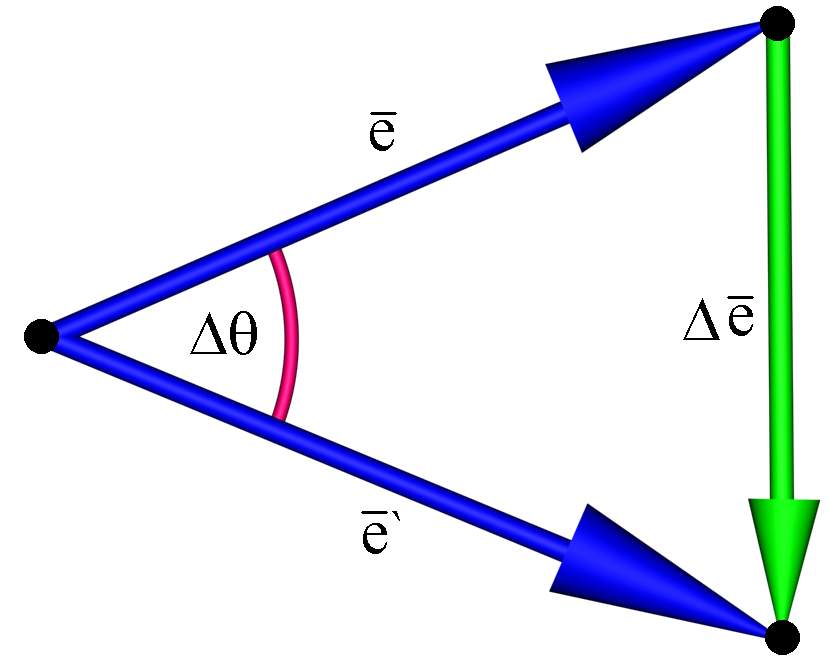
ΔOMM` OM OM` MM`=dS
При 
(т.к
)
8. Кривизна кривой, лежащей на поверхности оболочки. Вторая квадратичная форма.
Домножим правую и левую части скалярно на
;
;
коэф-ты
II
]
9. Кривизна нормального сечения. Связь между кривизной нормального и наклонного сечений. Теорема Менье.
-
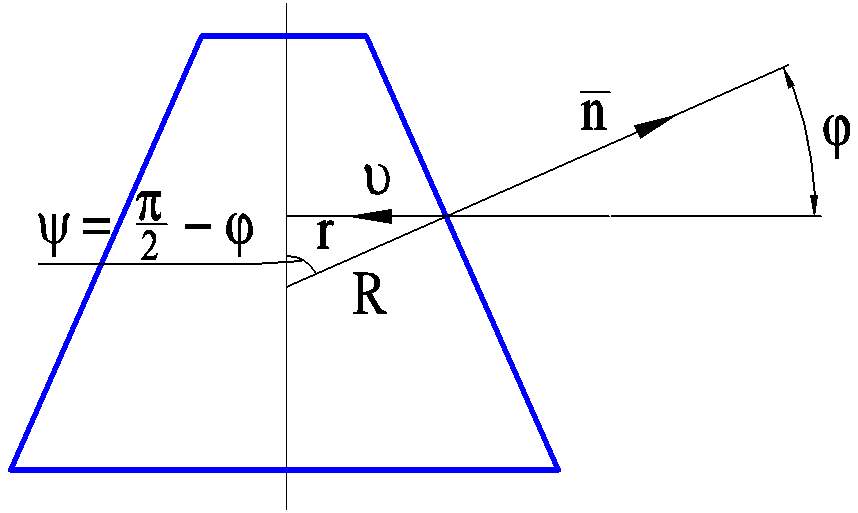
кривизна нормального сечения
φ=0
-- связь кривизны нормального и наклонного
сечений
10. Кривизны координатных линий, кручение.
Найдём кривизны координатных линий.
Возьмём нормальные сечения, проходящие через координатные линии.
-
Кривизны координатных линий
,
где
-кручение
срединной поверхности
Кручение – предел отношения естественного угла закручивания двух противоположных сторон малого элемента поверхности к расстоянию между этими сторонами
В пределе Δe2 направлен по (-n)
