Оглавление

1. Расчетная схема пластины - пластины, пластинки, мембраны, плиты. Основные гипотезы классической теории изгиба пластин. 7

Расчетная схема пластины 7

Основы теории пластин 7

Основные гипотезы. 7

2.Геометрические уравнения классической теории изгиба пластин Кирхгофа-Клебша. 8

Геометрические уравнения. 8

3.Характер напряженно-деформированного состояния тонкой пластины. Уравнения закона Гука. Погонные моменты. Связь усилий с перемещениями. 10

Уравнения закона Гука (Физические уравнения) 10

Погонные моменты 10

Физические уравнения. 11

Связь усилий с перемещениями 11

4.Уравнения равновесия. Разрешающие уравнения теории пластин в перемещениях - уравнения Софи Жермен - Лагранжа. Бигармонический оператор. 12

Уравнения равновесия 12

Разрешающие уравнения теории пластин в перемещениях - уравнения Софи Жермен - Лагранжа 13

5.Граничные условия. Парадокс Пуассона-Кирхгофа. 14

Граничные условия 14

Парадокс Пуассона-Кирхгофа 14

6.Цилиндрический изгиб пластин, чистый изгиб пластин, кручение пластин. 15

7.Расчет пластин при граничных условиях Навье. Двойной тригонометрический ряд. Свойства ортогональности и полноты системы функций. 17

8.Расчет пластин при граничных условиях Навье, случаи нагружения пластины сосредоточенной и распределенной нагрузкой. 20

9.Собственные колебания пластины шарнирно опертой по всему контуру. Нормирование форм колебаний по массе. 25

10.Расчет пластин при граничных условиях Леви. 27

11.Расчет пластин методом конечных разностей. Аппроксимация производных. Граничные условия. Законтурные точки. 29

Порядок аппроксимации: 31

Граничные условия. Законтурные точки. 32

12.Расчет тонких ортотропных пластин. Физические уравнения. Связь погонных усилий с перемещениями. 34

Физические уравнения. 35

13.Разрешающие уравнения теории ортотропных пластин в перемещениях. Конструктивно-ортотропные пластины. 37

Конструктивно-ортотропные пластины. 39

14.Теория пластин Тимошенко. Основные гипотезы. 40

Основные гипотезы: 40

15.Геометрические уравнения. Погонные силовые факторы. Разрешающие уравнения в перемещениях. 41

Элементы теории поверхностей 45

1.Расчетная схема оболочки. Основные определения. Срединная поверхность. Основные гипотезы классической теории оболочек. 45

Поверхность, равноудалённая от наружной и внутренней поверхностей оболочки, называется срединной поверхностью. 45

2.Координатный и векторный способ задания поверхности. 46

3.Материальные координаты. Семейства координатных линий на поверхности оболочки 48

4.Локальный координатный базис. Единичные векторы базиса. Параметры Ламе. 50

5.Первая квадратичная форма. Определение длин дуг координатных линий, геометрический смысл параметров Ламе. 52

6.Определение углов между единичными векторами. Ортогональные координаты. Первая квадратичная форма в ортогональных координатах. 54

7. Определение кривизны пространственной кривой. 55

8. Кривизна кривой, лежащей на поверхности оболочки. Вторая квадратичная форма. 57

9. Кривизна нормального сечения. Связь между кривизной нормального и наклонного сечений. Теорема Менье. 59

10. Кривизны координатных линий, кручение. 60

11. Экстремальные свойства кривизн. Главные кривизны и линии главных кривизн. Сопряженные системы координат. 62

12. Средняя и Гауссова кривизны. Классификация оболочек по значению Гауссовой кривизны. 64

Вопрос №13. 66

Формулы Вейнгартена дифференцирования единичных векторов. 66

Вопрос №14. 71

Соотношения Кодацци-Гаусса(без вывода). 71

1. Расчетная схема пластины - пластины, пластинки, мембраны, плиты. Основные гипотезы классической теории изгиба пластин.

Расчетная схема пластины

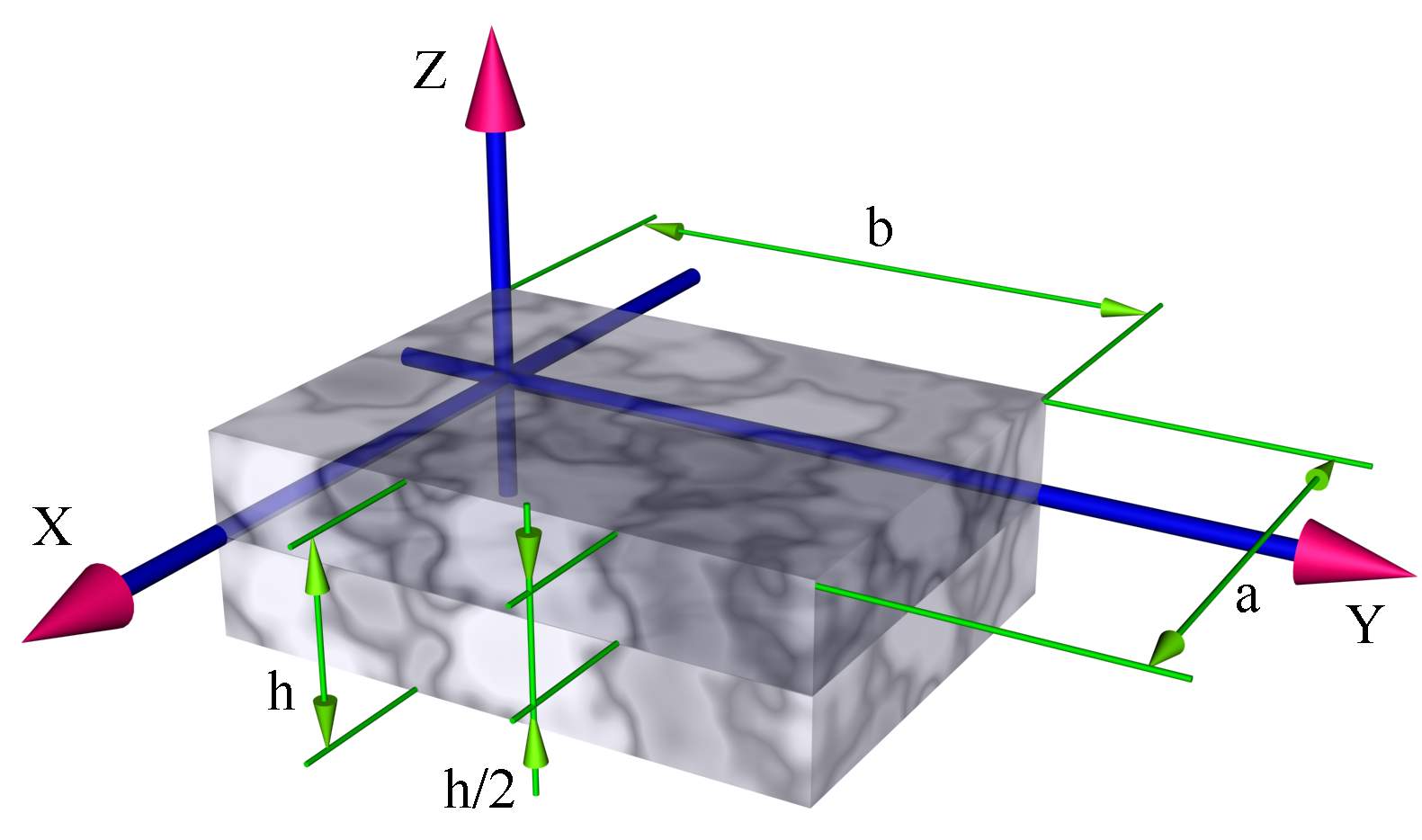
Основы теории пластин

Пластины - плоское тело одно из измерений которого много меньше двух других.

-линейная теория.

-геометрическая линейная теория.

-теория мембран.

Основные гипотезы.

1. Гипотеза прямых нормалей.

Прямолинейный элемент перпендикулярный срединной плоскости пластины до деформации, после деформации ос­тается перпендикулярным к деформации срединной плос­кости пластины и не изменяет своей длинны.

2. Гипотеза ненадавливания.

Нормальными напряжениями в слоях параллельных серединной плоскости можно пренебречь по сравнению с другими компонентами тензора напряжений.

2.Геометрические уравнения классической теории изгиба пластин Кирхгофа-Клебша.

Геометрические уравнения.

-кривизна линий x.

- кривизна линий y.

- кручение.

Геометрические уравнения.

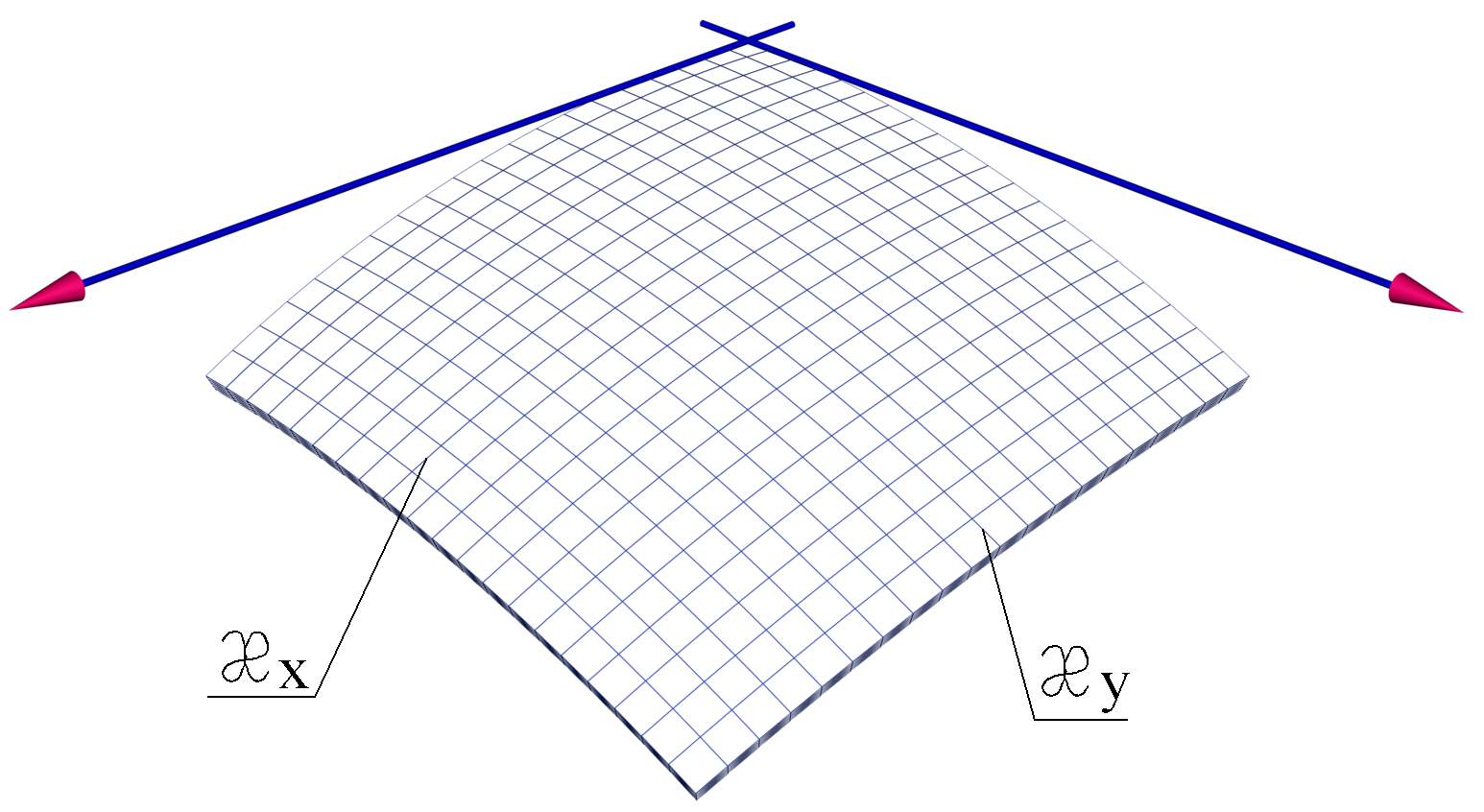
3.Характер напряженно-деформированного состояния тонкой пластины. Уравнения закона Гука. Погонные моменты. Связь усилий с перемещениями.

Согласно гипотезе ненадавливания напряжение вдоль оси z отсутствует.

Уравнения закона Гука (Физические уравнения)

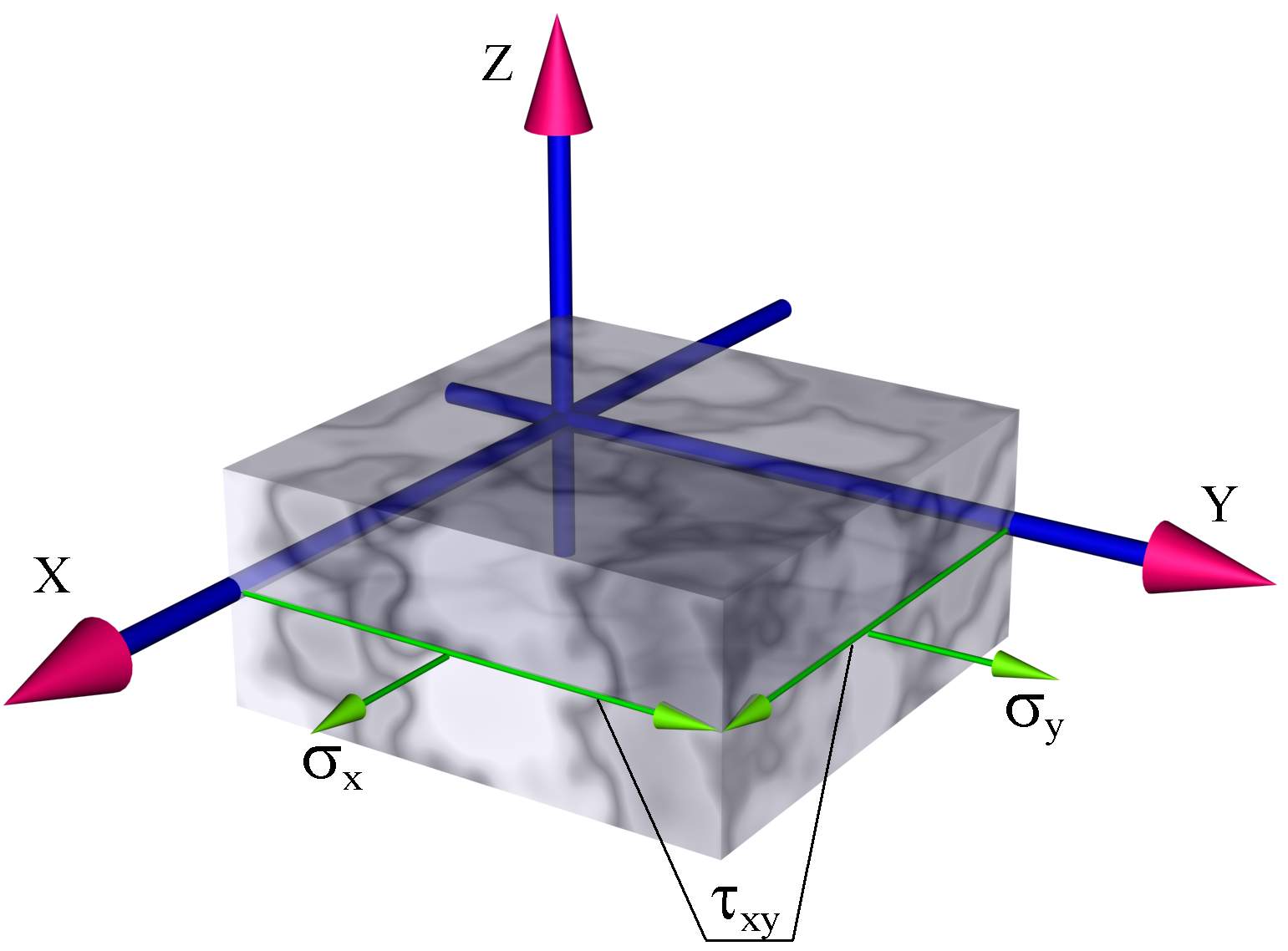
Погонные моменты

- цилиндрическая жесткость, т. е. это погонная балочная жесткость при изгибе в цилиндр.

Физические уравнения.

Связь усилий с перемещениями

;

Оператор Лапласа (гармонический оператор.):

;

4.Уравнения равновесия. Разрешающие уравнения теории пластин в перемещениях - уравнения Софи Жермен - Лагранжа. Бигармонический оператор.

Уравнения равновесия

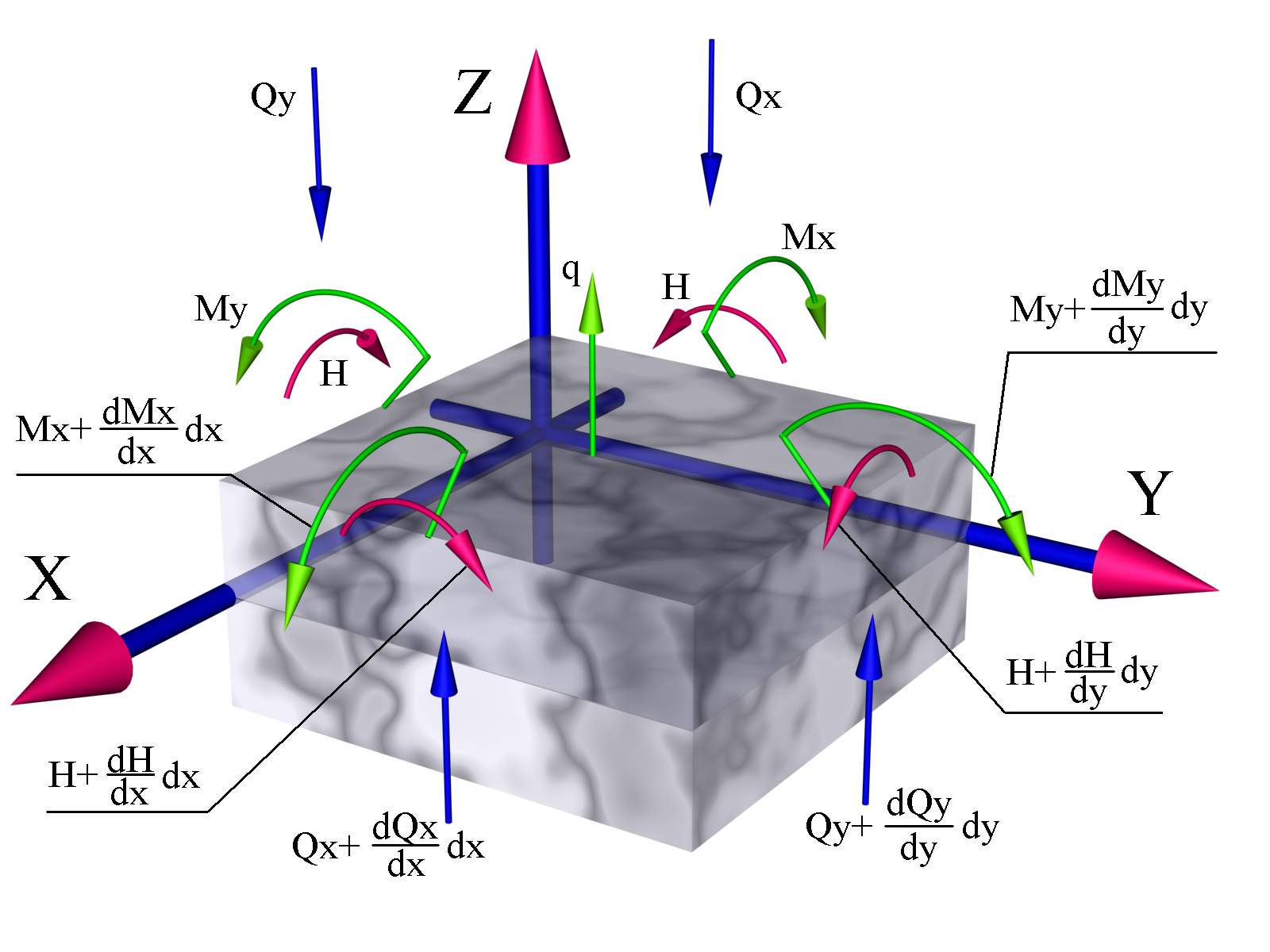
Поперечные силы рассматриваем как чисто статические силовые факторы.

Члены с тремя приращениями считаем б.м.

Разрешающие уравнения теории пластин в перемещениях - уравнения Софи Жермен - Лагранжа

– Двойной Лапласиан (Бигармонический оператор). , раскрываем

;

5.Граничные условия. Парадокс Пуассона-Кирхгофа.

Граничные условия

1. Заделка

2. Шарнир

3. Свободный край

Парадокс Пуассона-Кирхгофа

В случае свободного края, число граничных условий не соответствует порядку ДУ.

Преодоление: крутящий момент Н заменяется статически эквивалентной распределенной поперечной нагрузкой, которая добавляется к .

6.Цилиндрический изгиб пластин, чистый изгиб п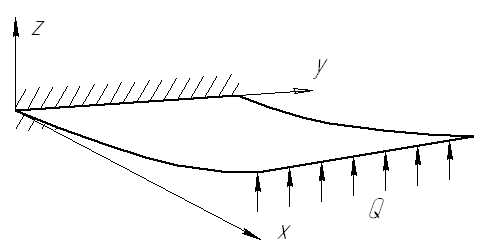 ластин, кручение пластин.

Задаемся функцией в виде полинома:

Граничные условия:

При

Силовые факторы на кромках:

7.Расчет пластин при граничных условиях Навье. Двойной тригонометрический ряд. Свойства ортогональности и полноты системы функций.

Граничные условия Навье – это условия шарнирного опирания по всему кон­туру.

1)

2)

3)

4)

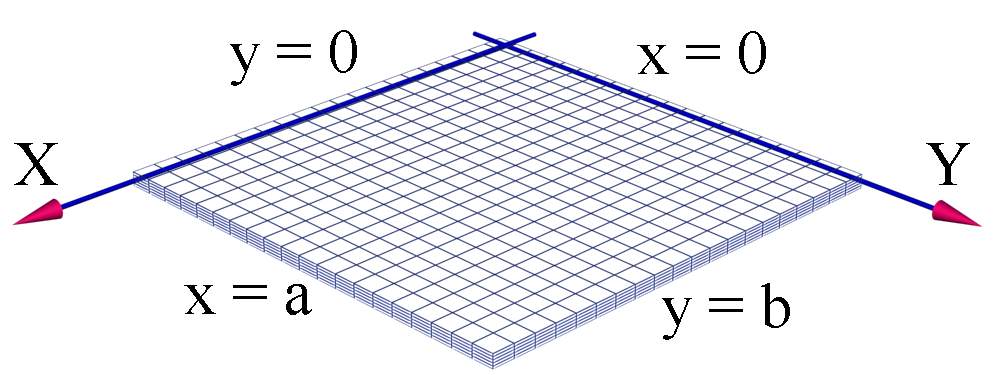
--функция, удовлетворяющая граничным усло­виям, но она не обязательно является решением дифференциального уравнения.

-из уравнения Софи-Жермен видно, что при подстановке W тождества не получается, поэтому q надо разложить в ряд по sin.

Условие ортогональности:

Заменим двойной интеграл двух кратным.

Произведем замену с использованием

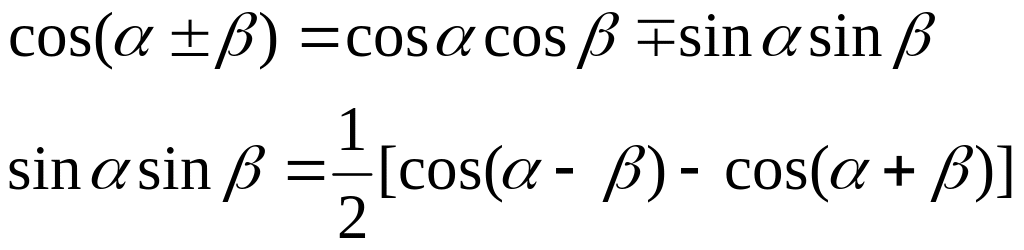
Получаем

Поучаем нагрузку в виде суммы ряда:

После замены окончательно получаем: