Головні напрямки на поверхні. Лінії кривини на поверхні. Теорема Родріга.

Нехай – регулярна поверхня, М – її фіксована точка. Напрямок з точки М на поверхні називається головним, якщо у цьому напрямку нормальна кривина приймає своє екстремальне значення, тобто мінімум або максимум. Треба зазначити, що в емболічних точках та точках сплощення головні напрямки невизначені, оскільки в цих точках в усіх напрямках нормальна кривина однакова. В інших точках існує два головні напрямки. З форми індикатриси кривизни бачимо, що ці напрямки співпадають з напрямками координатних осей в канонічній системі координат. Оскільки саме в цих напрямках величина приймає свої екстремальні значення.

З курсу аналітичної геометрії відомо, що напрямки і тоді і тільки тоді співпадають з напрямками осей канонічної системи координат кривих другого порядку, коли ці напрямки ортогональні і спряжені відносно першої квадратичної форми поверхні. Тому ортогональність напрямків записується через першу квадратичну форму наступним чином:

. (1)

А умова спряженості напрямків записується через другу квадратичну форму, оскільки вона і є квадратичною формою індикатриси кривини.

(2)

Приводячи подібні при отримаємо лінійну систему рівнянь відносно невідомих :

(3)

Головний напрямок – це ненульовий розв’язок системи. Однорідна система (3) тоді і тільки тоді має ненульові розв’язки, коли її визначник дорівнює нулю. Тим самим знаходимо умову для знаходження напрямку :

Стовпці цього визначника є сумами стовпців , тому цей визначник можна представити як суму чотирьох визначників. Виносячи зі стовпців отриманих визначників спільні множники маємо:

. (4)

. (5)

Отримали квадратне рівняння для знаходження головних напрямків. Це рівняння зручно записувати таким чином:

Якщо цей визначник розкрити за першим рядком, то отримаємо рівняння (4). Поділивши це рівняння на отримаємо рівняння для знаходження головних напрямків:

(6)

З цього рівняння знаходимо розв’язки:

(7)

Теорема Родріга: Нехай – регулярна поверхня, М – деяка її точка, – одиничний вектор нормалі, – вектор-функція поверхні . Тоді

1. Якщо напрямок з точки М є головним, то у цьому напрямку , де – нормальна кривина поверхні у напрямку .

2. Припустимо, що у деякому напрямку з точки М має місце співвідношення 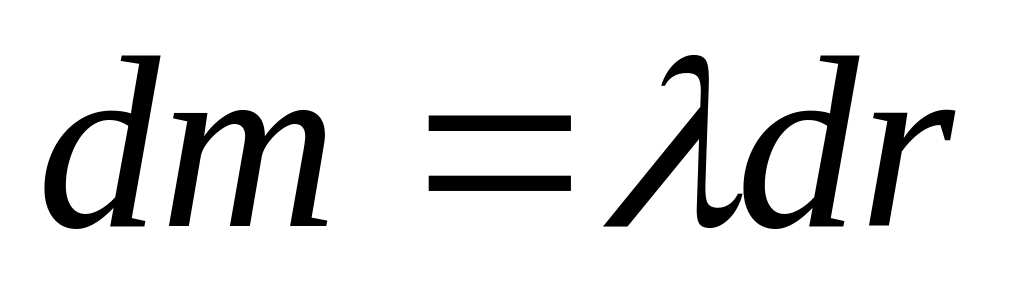, тоді , де – нормальна кривина точки М за напрямком .

Доведення: 1. Нехай – інший головний напрямок з точки М. Оскільки головні напрямки ортогональні , вони лежать у дотичній площині поверхні у точці М. Оскільки вектор-функція має постійну довжину 1, то вона ортогональна до свого диференціала і значить лежить у дотичній площині. Таким чином вектори компланарні і лежать у дотичній площині. Тому вектор можна лінійно через :

2. Нехай – напрямок, ортогональний до напрямку . Тоді . Помножимо обидві частини рівняння на вектор і отримаємо:

Що є умовою спряженості напрямків . А якщо напрямки спряжені відносно другої квадратичної форми і взаємно ортогональні, то вони і є головними напрямками. Помножимо тепер рівняння скалярно на вектор :

Нехай – регулярна поверхня. Крива на поверхні називається лінією кривини, якщо у кожній її точці напрямок цієї кривої з цієї точки є головним.

Розв’язки (7) рівняння (6) можна розглядати як диференційні рівняння для знаходження ліній кривини. Інтегруючи ці рівняння, маємо: – внутрішні рівняння ліній кривини у неявній формі. Значення параметрів знаходяться з початкової умови: ці ліній проходять через деяку фіксовану точку .

Координатні лінії з напрямками визначають головні напрямки, якщо їх напрямки є взаємно ортогональними і спряженими відносно другої квадратичної форми.

Умова ортогональності записується: , умова спряженості – .

(8)

Тобто, якщо координатні лінії є лініями кривини, то в усіх точках поверхні повинні виконуватися умови (8).