Друга квадратична форма регулярної поверхні. Формули для обчислення коефіцієнтів.

Нехай – регулярна поверхня з вектор-функцією . Тоді в кожній точці поверхні визначена дотична площина цієї поверхні, що паралельна векторам . Тому в кожній точці поверхні визначена вектор-функція – одиничний вектор нормалі поверхні у точці . Тоді є квадратичною формою від змінних , ці форму називають другою квадратичною формою поверхні і позначають (1)

Також використовують позначення .

Оскільки , то згідно (1) маємо:

Скористаємось лінійністю скалярного добутку, отримаємо:

.

Відмітимо, що коефіцієнти другої квадратичної форми є числовими функціями від , які у кожній точці поверхні приймають свої однозначно визначені значення.

Якщо точка фіксована, тоді коефіцієнти є сталими числами і значення залежать тільки від .

Знайдемо тепер вирази для коефіцієнтів , що залежать тільки від вектор-функцій . Знайдемо спочатку вектор-функції :

Таким чином:

(2)

Оскільки дотична площина цієї поверхні паралельна векторам , , то вектор лежить у дотичній площині, а оскільки нормаль перпендикулярна дотичній площині, то перпендикулярний до одиничного вектору нормалі , тоді , а значить і . Обчислимо диференціал у лівій частині цього рівняння:

Таким чином:

З формули (1): (3)

Підставляючи (2) у (3), скориставшись лінійністю скалярного добутку, маємо:

.

Отримали формули для коефіцієнтів другої квадратичної форми:

(4)

(5)

(6)

Припустимо, що коефіцієнти першої квадратичної форми відомі:

(7)

Нехай поверхня задана явним рівнянням , – параметричне рівняння, враховуючи (6), маємо:

(8)

.

Кривина нормального перерізу поверхні. Нормальна кривина поверхні в заданому напрямку.

Нехай – регулярна поверхня з вектор-функцією , P – деяка точка, – одиничний вектор нормалі. .

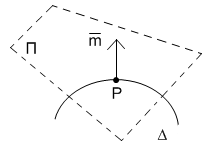
Проведемо через і точку P деяку площину. – нормальний переріз поверхні у точці Р. є кривою на поверхні , тому вона визначає напрямок (координати деякого напрямного вектора дотичної кривої у базисі ).

Оскільки П однозначно визначається точкою Р, вектором і напрямним вектором дотичної кривої ( який в свою чергу однозначно визначає ), то у заданому напрямку існує тільки один нормальний переріз поверхні у точці Р.

Теорема Меньє: Нехай деяка крива на поверхні , що проходить через точку Р. Нехай внутрішнє рівняння цієї кривої віднесено до параметра : , – одиничний вектор нормалі, – одиничний вектор головної нормалі кривої у точці Р, – кут між і . Тоді

(1)

де – кривина у точці Р, , – напрямок у точці Р.

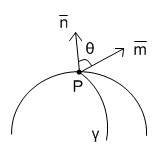
Доведення: Оскільки внутрішнє рівняння кривої віднесено до параметра , то її вектор-функція має вигляд:

, де – вектор-функція поверхні. За формулою Френе:

, – кривина .

.

Таки чином:

.

Причому, оскільки , то , і тому напрямок є напрямком кривої у точці Р.

Величину називають нормальною кривиною поверхні у точці P у напрямку . Якщо точка P фіксована, то коефіцієнти є сталими числами і тому значення залежить тільки від . Тому у фіксованій точці поверхні Р, при заданому напрямку , визначається однозначно.

Твердження: Нехай – регулярна поверхня, P – деяка її точка, – нормальний переріз поверхні у напрямку , тоді кривина нормального перерізу у точці P з точністю до знака співпадає з нормальною кривиною поверхні у точці P у напрямку .

Доведення: Нехай П – площина, що утворює нормальний переріз . Тоді – плоска крива, що лежить у площині П. Нехай – одиничний вектор дотичної кривої і – одиничний вектор головної нормалі кривої . Тоді . Крім того за означенням нормального перерізу . Тоді за малюнком . А оскільки лежить у дотичній площині поверхні у точці Р, то . Таким чином паралельні одній і тій же площині П і ортогональні до одного і того ж вектора , що також паралельний площині П. Звідси випливає . Нехай , тоді і з попередньої теореми випливає: .