
- •Регулярні поверхні.
- •Різні аналітичні засоби задання регулярних поверхонь.
- •Криві та поверхні. Напрямки на поверхні.
- •Дотична площина та нормаль поверхні.
- •Перша квадратична форма регулярної поверхні
- •Формули для обчислення коефіцієнтів I(d)
- •Довжина дуги кривої на поверхні
- •Кут між кривими на поверхні
- •Площа простого шматка регулярної поверхні
- •Друга квадратична форма регулярної поверхні. Формули для обчислення коефіцієнтів.
- •Кривина нормального перерізу поверхні. Нормальна кривина поверхні в заданому напрямку.
- •Індикатриса кривини. Класифікація точок регулярної поверхні.
- •Асимптотичні напрямки. Асимптотичні лінії на поверхні.
- •Головні напрямки на поверхні. Лінії кривини на поверхні. Теорема Родріга.
- •Головні кривини. Середня і повна кривина.
- •Формули Ейлера.
- •Дериваційні формули.
- •Формули Гауса-Петерсена-Кодаци. Теорема Боне.
- •Література
Перша квадратична форма регулярної поверхні
Нехай
– регулярна поверхня,
– її вектор-функція, що віднесена до
криволінійних координат
![]() ,
тоді диференціал вектор-функції
(тобто лінійна частина приросту цієї
функції в ряду Тейлора) має вигляд:
,
тоді диференціал вектор-функції
(тобто лінійна частина приросту цієї
функції в ряду Тейлора) має вигляд:
![]() (1), де
(1), де
![]() – частинні похідні,
– довільні дійсні числа, що можуть
приймати скільзавгодно малі значення.
– частинні похідні,
– довільні дійсні числа, що можуть
приймати скільзавгодно малі значення.
Скалярний квадрат
– це:
![]() (2) називається першою квадратичною
формою поверхні
.
(2) називається першою квадратичною
формою поверхні
.
Знайдемо коефіцієнти цієї квадратичної форми. Підставляючи (1), (2), маємо:
![]() .
.
Таким чином
![]() дійсно квадратична форма від змінних
з коефіцієнтами:
дійсно квадратична форма від змінних
з коефіцієнтами:
![]() .
.
Відмітимо, що
взагалі коефіцієнти
– це вектор-функції від
.
Але якщо точка поверхні фіксована, то
коефіцієнти
є сталими числами і значення квадратичної
форми визначаються значеннями змінних.
Відмітимо, що квадратична форма
є додатньовизначеною, що випливає з
(2), оскільки скалярний добуток приймає
тільки додатні значення, крім випадку
коли
![]() ,
а це можливо тільки коли
,
а це можливо тільки коли
![]() ,
оскільки
не є паралельними. З додатньої визначеності
випливає, що у будь-якій точці
:
,
оскільки
не є паралельними. З додатньої визначеності
випливає, що у будь-якій точці
:
![]() .
.
Відмітимо, що крім
позначення (2) для
використовують також позначення
![]() .
Розглядають також
в якій змінними виступають похідні
внутрішнього рівняння кривої
.
Розглядають також
в якій змінними виступають похідні
внутрішнього рівняння кривої
![]() .
Крім того, будують
за допомогою диференціалів різних
вектор-функцій
.
Крім того, будують
за допомогою диференціалів різних
вектор-функцій
![]() .
.
Формули для обчислення коефіцієнтів I(d)
Припустимо, що поверхня задана параметричним рівнянням:
.
Тоді частинні
похідні мають координати
![]() .
Тоді
.
Тоді
![]() (3)
(3)
Припустимо, що поверхня задана явною функцією: . Тоді
![]() .
.
Тоді за формулами (3) маємо:
![]() (4)
(4)
Припустимо, що поверхня задана неявним рівнянням: . Оскільки поверхня регулярна, то в будь-якій точці хоча б одна з частинних похідних функції
 не дорівнює нулю. Припустимо, що у
точці, де розглядається
,
частинна похідна
не дорівнює нулю. Припустимо, що у
точці, де розглядається
,
частинна похідна
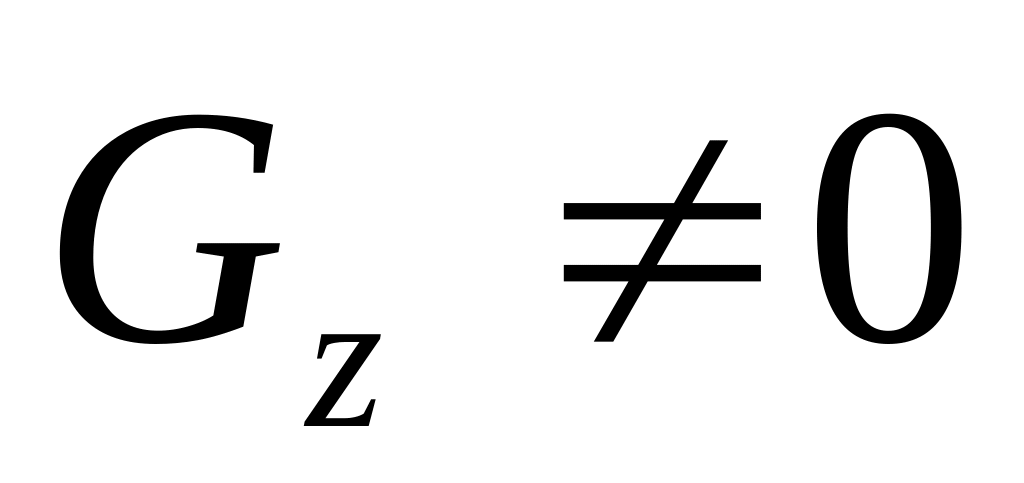 .
Тоді згідно теореми про неявну функцію
у деякому околі цієї точки поверхню
можна задати явною функцією
.
Причому частинні похідні будуть мати
вигляд:
.
Тоді згідно теореми про неявну функцію
у деякому околі цієї точки поверхню
можна задати явною функцією
.
Причому частинні похідні будуть мати
вигляд:
 .
Тоді з формули (4) отримаємо:
.
Тоді з формули (4) отримаємо:
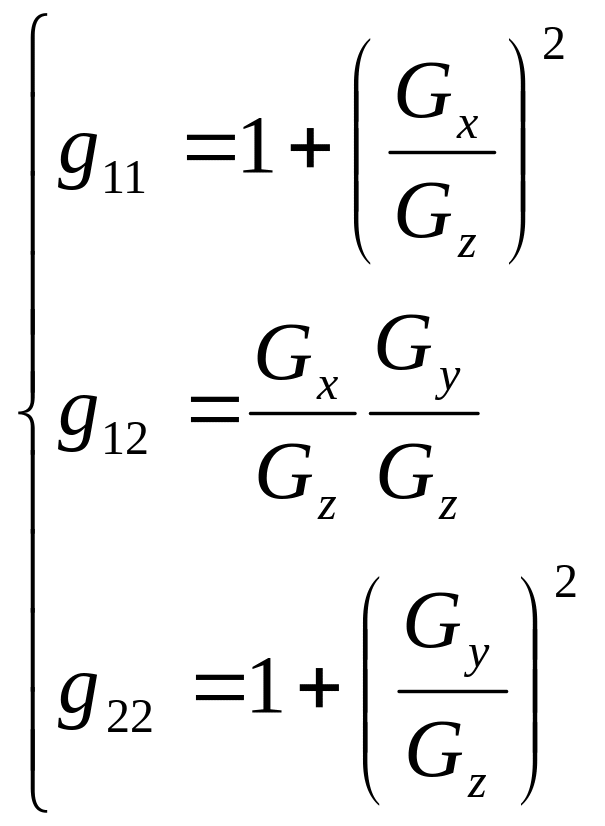 (5)
(5)
Довжина дуги кривої на поверхні
Нехай – поверхня, – її вектор-функція, – крива, що лежить на поверхні.
![]() – внутрішнє
рівняння кривої
.
Тоді вектор-функція кривої має вигляд:
– внутрішнє
рівняння кривої
.
Тоді вектор-функція кривої має вигляд:
![]() (1).
(1).
Довжина дуги
кривої
,
що знаходиться між точками
![]() обчислюється за формулою:
обчислюється за формулою:
 (2).
(2).
Підставляючи (1) в (2) маємо:

 .
.
З формули для обчислення довжини дуги кривої на поверхня випливає, що диференціал довжини дуги кривої на поверхні має вигляд:
![]() .
.
