3.3 Проверка прочности шпоночных соединений
Задачей данного параграфа является проверка шпонок по напряжениям смятия.
Для соединения вала с деталями, передающими вращение (шкивы, муфты) наиболее часто применяют призматические шпоночные соединения.
Конструктивно применяем стандартные призматические шпонки со скругленными концами.
Схема шпоночного соединения
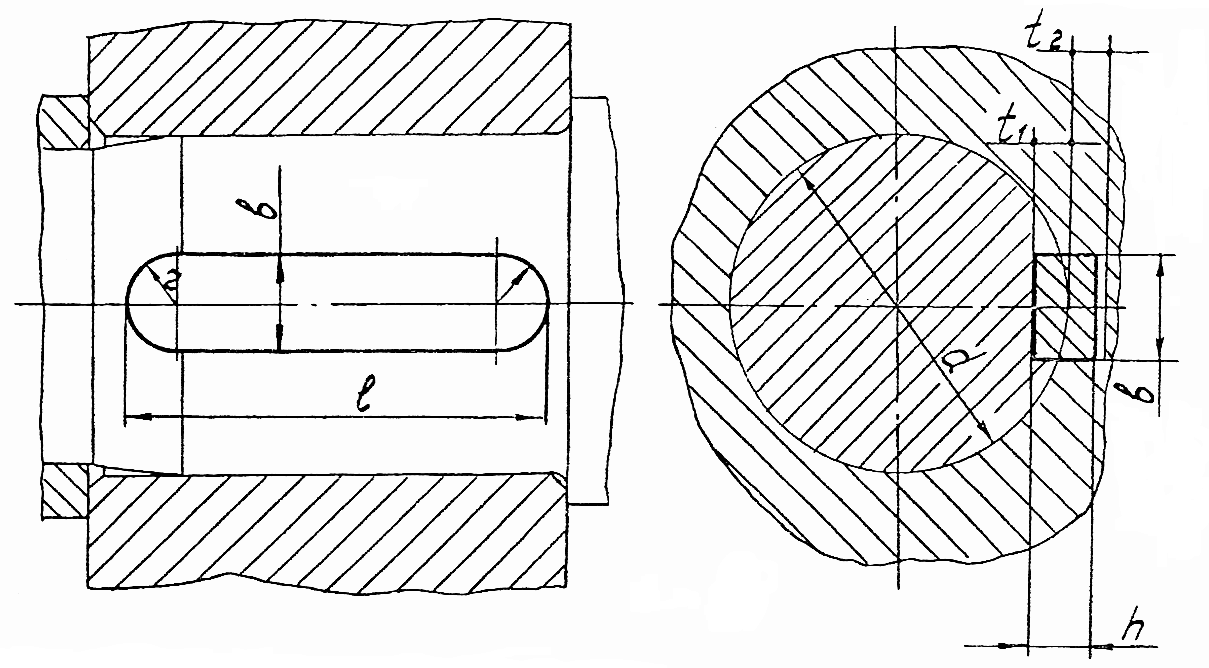
Рис. 5
Из двух шпонок на валу наиболее нагружена шпонка под колесом 3, т.к. меньше диаметр вала, и поэтому меньше размеры поперечного сечения шпонки. Проверку будем проводить по формуле (3.3.1):
,
где
F
–
нагрузка;
- площадь смятия.
;
.
Для шпонки с плоскими концами l=lраб.
где
Т - крутящий момент на валу,
;
d - диаметр вала, мм;
h - высота шпонки, мм;
-
глубина паза вала, мм;
-
рабочая длина шпонки;
b - ширина шпонки, мм;
-
допускаемое напряжение на смятие, Па.
Материал
шпонки Сталь 45 нормализованная, поэтому
допускаемое напряжение при стальной
ступице [1, с. 310]
=100
120
МПа.
Размеры шпонки [1, с. 169] 10 8 28 ГОСТ 23360-78, глубина паза вала =5 мм.
Подставляя численные значения в выражение (3.3.2), получим
.
Напряжение
смятия больше допускаемого значения,
поэтому устанавливаем две шпонки под
углом
.
Тогда напряжение смятия будет равно
Две шпонки, установленные под углом 1800 обеспечивают нормальную передачу момента вращения.
Проверка шпонки под колесом 2
Материал шпонки Сталь 45 нормализованная, поэтому допускаемое напряжение при стальной ступице [1, с. 310] =100 120 МПа. Размеры шпонки 16 10 70 ГОСТ 23360-78, глубина паза вала =6 мм.
Шпонка обеспечивает нормальную передачу момента вращения.
3.4 Проверочный расчёт вала
Целью данного параграфа является проверка результатов, полученных в параграфе 3.1.
Циклы изменения напряжений для вала
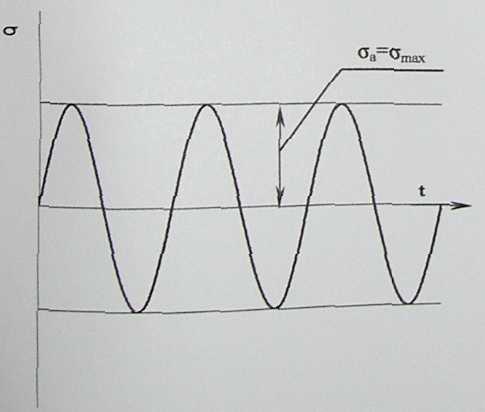
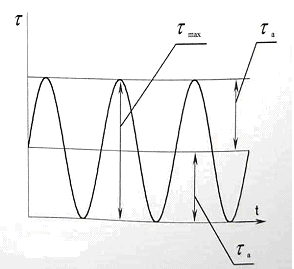
Рис. 6
Материал
вала - сталь 45 нормализованная, предел
прочности [1, с. 34]
.
Пределы выносливости по нормальным
напряжениям [1, с.313]
и по касательным
.
Определим коэффициент запаса прочности s и сравним его с допускаемым [s].
Назначаем
нормативный запас прочности
Исходя из эпюр крутящих и изгибающих моментов и конструкции вала, выбираем два наиболее опасных сечения для проверки.
Сечение а-а. Диаметр вала в этом сечении d=50 мм. Концентрация напряжений обусловлена наличием шпоночной канавки. Ширина шпонки в этом сечении b=14 мм, глубина паза =5,5 мм.
Найдём изгибающий момент в горизонтальной плоскости
,
(3.4.1)
подставляя численные значения, получим
.
Найдём изгибающий момент в вертикальной плоскости
,
(3.4.2)
подставляя численные значения, получим
.
Суммарный изгибающий момент в сечение а-а найдём по формуле
,
(3.4.3)
подставляя численные значения, получим
Определяем коэффициент запаса прочности [1, c. 162]
(3.4.4)
Коэффициент запаса прочности по нормальным напряжениям будем рассчитывать по формуле (3.4.5)
где
- предел выносливости стали при
симметричном цикле изгиба, Па;
-
эффективный коэффициент концентрации
нормальных напряжений [1, c.
165];
-
масштабный фактор для нормальных
напряжений [1, c.
166];
β
- коэффициент шероховатости поверхности
(
)
-
амплитуда цикла нормальных напряжений,
Па;
-
среднее значение напряжения цикла, Па;
-
коэффициент чувствительности материала
по изменению цикла нормальной нагрузки;
коэффициент выбираем по рекомендации [1, с. 164] и считаем =0,2;
Коэффициент и выбираем по рекомендации [1, с. 165, 166] и считаем =1,6, =0,8.
Так как осевая нагрузка отсутствует, то =0.
Амплитуду нормальных напряжений найдём по формуле
(3.4.6)
-
осевой момент сопротивления в сечении
вала, мм3.
Момент сопротивления нетто при изгибе найдём по соотношению (3.4.7) [1, c. 165]
подставляя численные значения, получим
.
подставляя численные значения в (3.4.6), получим
Подставляя численные значения в выражение (3.4.5), получим
Коэффициент запаса прочности по касательным напряжениям будем рассчитывать по аналогичной формуле (3.4.8)
где
- предел выносливости стали при
симметричном цикле кручения, МПа;
-
эффективный коэффициент концентрации
касательных напряжений;
-
масштабный фактор для касательных
напряжений;
-
среднее напряжения цикла, МПа;
-
среднее напряжение цикла кручения, МПа;
коэффициент
выбираем по рекомендации [1, с. 166] и
считаем
=0,1.
Коэффициент и выбираем по рекомендации [1, с. 165, 166] и считаем =1,5, =0,7;
среднее напряжение цикла касательных напряжений найдём по соотношению (3.4.9)
,
Т2 – крутящий момент;
-
полярный момент сопротивления вала.
Подставляя численные значения, получим
.
Подставляя численные значения в выражения (3.4.8), получаем
Подставляя численные значения в формулу (3.4.4), получим
.
Запас прочности обеспечен.
Сечение в-в. Диаметр вала в этом сечении d=50мм. Концентрация напряжения в этом сечении обусловлена посадкой подшипника с гарантированным натягом [1, c. 314].
Найдём изгибающий момент в горизонтальной плоскости
(3.4.9)
подставляя численные значения, получим
.
Найдём изгибающий момент в вертикальной плоскости
(3.4.10)
подставляя численные значения, получим
Суммарный изгибающий момент в сечение Б-Б найдём по формуле
(3.4.11)
подставляя численные значения, получим
.
Осевой момент сопротивления найдём по соотношению
(3.4.12)
подставляя численные значения, получим
.
Полярный момент сопротивления найдём по формуле
(3.4.13)
подставляя численные значения, получим
.
Амплитуду и среднее значение цикла касательных напряжений найдём по соотношению
(3.4.14)
подставляя численные значения, получим
.
Амплитуду нормальных напряжений найдём по формуле
(3.4.15)
подставляя численные значения, получим
.
Отношения
найдём по рекомендации [1, с. 166] и будем
считать равным
=2,55
Отношение
найдём по формуле
(3.4.16)
подставляя численные значения, получим
.
Найдём коэффициенты запаса прочности по нормальным и касательным напряжениям по формулам (3.4.17) и (3.4.18):
подставляя численные значения, получим
;
.
Результирующий коэффициент запаса прочности для сечения в-в находим по формуле (3.4.19):
подставляя численные значения, получим
.
Запас прочности обеспечен.