3. Проектирование промежуточного вала на опорах качения

Цель: проведение предварительного (проектировочного) расчета вала.

3.1 Предварительный расчет вала.

Цель: определение диаметра выходного конца вала 2 ( диаметра под шестерню 3) и последующее назначение диаметра под зубчатое колесо и опорные подшипники.

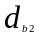- диаметр вала II

- момент на промежуточном валу.

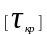- допускаемое касательное напряжение на кручение.

Полученное значение округляем по рекомендации [1, с. 161], .

Так как диаметр d_ВК должен быть кратен 5, то примем .

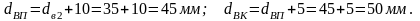
3.2. Выбор и проверочный расчет

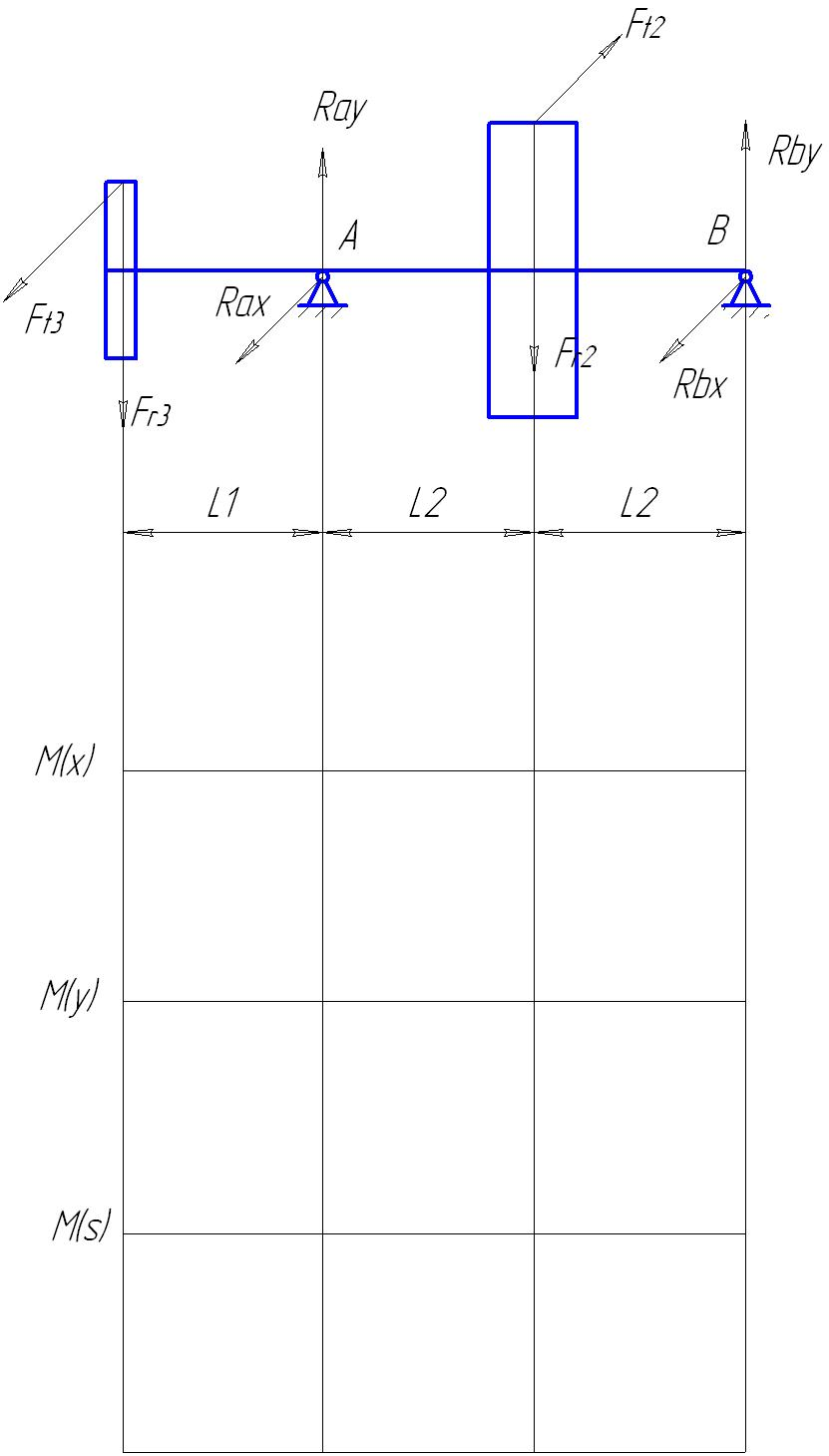
Целью данного раздела является определение реакций, действующих в опорах с построением эпюр изгибающих моментов и моментов вращения. Проверка подшипников на долговечность.

Расчетная схема вала

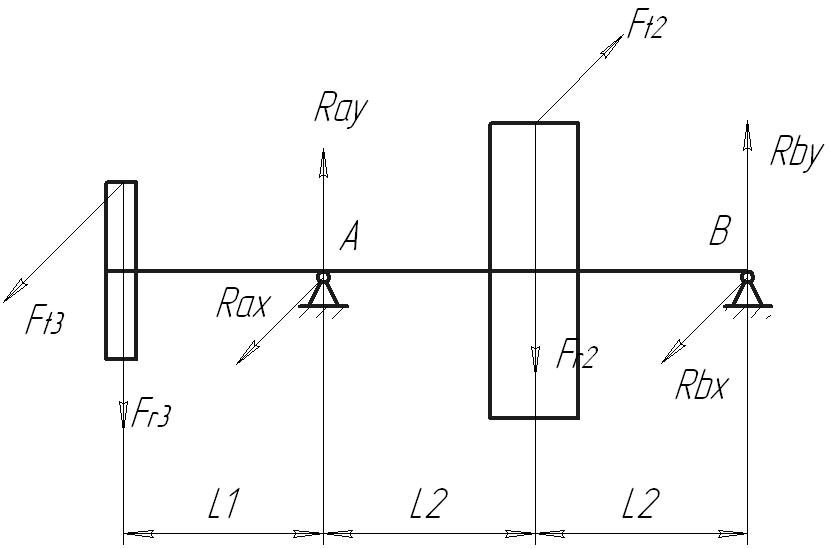
Рис. 3

3.2.1. Расчёт реакций, действующих в опорах и построение эпюр изгибающих моментов

Вал рассматривается как балка, лежащая на опорах. В сцеплениях действуют осевые силы.

, - окружные силы, действующие соответственно на колесо зубчатое колесо и шестерню, Н;

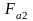- осевая сила, Н;

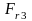, - радиальные силы, действующие соответственно на зубчатое колесо и шестерню, Н;

, - реакции в опоре А, Н;

, - реакции в опоре В, Н.

На зубчатое колесо 2 действуют осевая, окружная и радиальная силы. Их численные значения были найдены в пункте 2.2.2. На шестерню 3 действуют только окружная и радиальная силы, т.к. открытая передача прямозубая. Найдём их по соотношениям аналогичным соотношениям для колеса 2:

Определим диаметр шестерни 3:

.

Найдем численные значения и :

.

Рассчитаем длины участков вала , , :

;

;

.

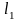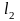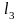В опорах А и В возникают реакции. Разложим их на составляющие, направленные по осям X и Y, т.е. будем считать, что в опоре А возникают реакции , ,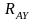 а в опоре В - , . Найдём их из уравнения вала .

Найдём сумму изгибающих моментов, действующих по оси X, относительно опоры А

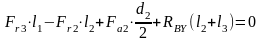
Следовательно ;

Подставляя численные значения, получим

Н.

Найдём сумму изгибающих моментов, действующих по оси Y, относительно опоры А

,

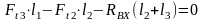т.е. ,

подставляя численные значения, получим

.

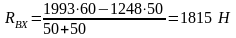Запишем аналогичные отношения для опоры В

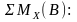
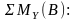
Выразим из этих уравнений

,

подставляя численные значения, получим

;

.

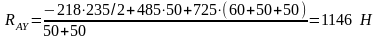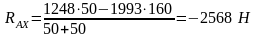Построим эпюры изгибающих и крутящих моментов.

Найдём суммарные реакции в опорах А и В по формулам

, , (3.2.1.1)

подставляя численные значения, получим

Эпюры изгибающих и крутящих моментов

3.2.2 Проверка долговечности подшипников

Реакция в опоре А больше, следовательно будем вести расчёт для подшипника, находящегося на ней. Используем радиально-упорный подшипник качения средней серии 46310 ГОСТ 831-75 с параметрами: внутренний диаметр d=45 мм, внешний диаметр D=80мм, ширина B=19 мм, динамическая грузоподъёмность C=31,2 кН, кН[1, с 400].

Эквивалентную нагрузку будем искать по формуле

, (3.2.2.1)

где V- коэффициент приращения, при вращении внутреннего колеса, [1, c. 212];

- коэффициент, учитывающий влияние вида нагрузки на подшипник;

- коэффициент, учитывающий влияние рабочей температуры подшипника;

- суммарная реакция в опоре А.

Значение коэффициентов выбираем по рекомендации [1, с. 214] и считаем равными =1,4; =1,05.

Подставляя численные значения в выражение (3.2.2.1), получим

Номинальную долговечность подшипника или ресурс L найдём по соотношению

(3.2.2.2)

где с - динамическая грузоподъемность (см. справочник);

- эквивалентная нагрузка;

m – показатель степени для шариковых подшипников (m=3),

подставляя численные значения, получим

.

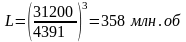Переведём долговечность в часы [1, с. 211]

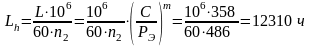
Согласно техническому заданию ресурс равен 3000 часов, найденный ресурс больше, следовательно, подшипник удовлетворяет требованиям по долговечности.