2. Моделирование экономических процессов на базе временных рядов

Решение любой задачи по анализу и прогнозированию временных рядов, как уже было ранее сказано, обычно начинается с построения графика динамики исследуемого показателя и визуализации динамического ряда. При этом не всегда можно явно выделить наличие тенденции и циклических компонент ряда.

В этих случаях прежде, чем пе­рейти к подробной оценке тенденции и его выделению, нужно выяснить наличие или отсутствие закономерностей в исследуемом процессе.

Основные подходы к оценке существования регулярных компонент ряда основаны на статисти­ческой проверке гипотез. В частности, одним из критериев выявления регулярных компонент ряда является проверка гипотезы о случайности ряда.

В практике, в качестве методологии проверки наличия тенденции в ряду, используют следующие методы:

- метод восходящих и нисходя­щих серий;

- метод оценки медианы выборки;

- метод Фостера-Стюарта и др.

Рассмотрим эти наиболее часто используемые на практике критерии проверки наличия/отсутствия трендовой компоненты временного ряда.

2.1. Методы оценки гипотезы о существовании тенденции. Метод восходящих и нисходя­щих серий.

Данный метод базируется на использовании критерия, оценивающего структуру и параметры некоторого дополнительно построенного промежуточного ряда, состоящего из восходящих и нисходящих серий. Этот дополнительный ряд строится на базе исходных данных.

Сформулируем методику оценки наличия или отсутствия тренда в ряду, в виде следующего алгоритма.

1. Определяется выборка статистических наблюдений за изменениями исследуемого показателя во времени – динамический ряд вида (y₁,y₂,…,у_n).

2. Строится диаграмма динамического ряда по полученной выборке.

3. Строится промежуточный ряд δ, в котором уровень ряда определяется по следующему правилу

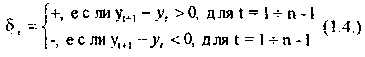(2.1)

Индекс i может изменяться от 1 до (п - 1). В случае, когда последую­щее наблюдение окажется равным предыдущему, учитывается только одно наблюдение.

Таким образом, элементы этого промежуточного ряда принимают значение δ = "+", если последующее значение уровня ряда y_t-1 больше преды­дущего у_t и δ = "–" в противном случае.

Строится промежуточная таблица следующего вида

№ п/п	1	2	3	….	n
Исследуемый показатель	y1	y2	y3	….	yn
Промежуточный ряд	δ1	δ2	δ3	….	δn

4. Для полученного промежуточного ряда, рассчитываются следующие количественные показатели ряда δ, такие как:

- υ(n) - число серий в совокупности δ_i (i = 1…(n - 1)),

- τ_i – длина каждой серии.

Под серией понимаем последовательность подряд идущих одинаковых значений промежуточного ряда – знаков «+» или «-». Один плюс или один минус также считается серией. Таким образом, формируются восходящие (из «+») и нисходящие (из «-») серии промежуточного ряда δ.

5. Определяется τ_max(n) - протяженность самой длинной серии по формуле

τ_max(n) = max [τ_1, τ_2, τ_3,…,τ_m].

6. Проводится проверка гипотезы о слу­чайности ряда (при отсутствии систематической составляющей). Проверка основывается на применении решающего правила вида: протя­женность самой длинной серии не должна быть слишком большой, а общее число серий - слишком маленьким. Поэтому, если нарушается хотя бы одно из указанных условий, то гипотеза об отсутствии тренда (гипотеза о случайности) отвергается для 5% уровня значимости (с дове­рительной вероятностью 0,95).

Формальные условия решающего правила определяются следующими неравенствами

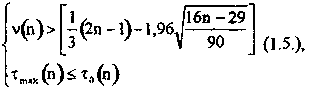(2.2)

где: n - длина временного ряда; υ(n) - число серий в ряду δ; τ_max(n) – размер (длина) самой длин­ной серии.

Нормативное (критическое) значение τ_o(n) выбирается по специальной таблице, причем τ_o(n) – это табличное значение, зависящее от n - длины исход­ного ряда и оно находится по табл.2.1.

Таблица 2.1. Выборка таблицы критических значений τ_o(n)

Длина ряда	n < 26	26 < n < 153	153 < n < 170
Значение τo(n)	5	6	7

Для первого правила (неравенства) в системе (2.2), квадратные скобки в правой части неравенства, означают це­лую часть числа, т.е. это целое число, ближайшее к А и не превосходящее его.

Рассмотрим пример оценки наличия или отсутствия тенденции.

Пример 2.1. Даны наблюдения стоимости акции по периодам наблюдения (месяц). Определить методом восходящих/нисходящих серий наличие или отсутствие тенденции в ряду наблюдений. Данные приведены в табл.2.2.

Таблица 2.2. Данные ряда наблюдений за уровнем курса акций

t	y	t	y
1	37	13	8
2	33	14	41
3	15	15	43
4	36	16	31
5	26	17	42
6	24	18	47
7	16	19	51
8	33	20	21
9	44	21	26
10	34	22	32
11	63	23	37
12	52	24	42

Решение.

1. Проводится наблюдение исследуемого признака. Определяем совокупность показателей, ранжированных в хронологической последовательности.

2. На основании исходных наблюдений делаем графический анализ ряда (рис.2.1).

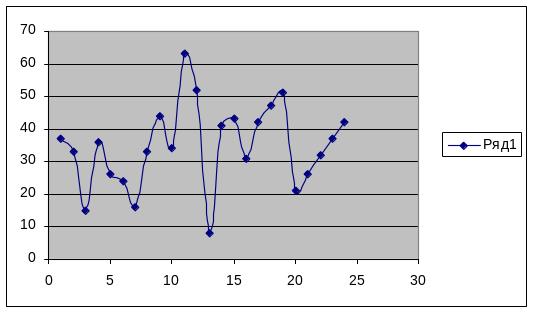
Рисунок 2.1. График анализа динамического ряда курса акций

3. Строим промежуточный ряд δ по исходным данным из вычисленных значений, согласно правилу (2.1), т.е. значения этого ряда принимают знак «+», если последующие значения ряда больше предыдущего, и знак «-», иначе.

4. Формируется промежуточная таблица (табл.2.3) и определяется количество серий и длина серии, которая определяется как количество знаков в серии.

Таблица 2.3. Таблица промежуточных расчетов

t	y	δ	ν	τ
1	37
2	33	-	1	2
3	15	-
4	36	+	2	1
5	26	-	3	3
6	24	-
7	16	-
8	33	+	4	2
9	44	+
10	34	-	5	1
11	63	+	6	1
12	52	-	7	2
13	8	-
14	41	+	8	2
15	43	+
16	31	-	9	1
17	42	+	10	3
18	47	+
19	51	+
20	21	-	11	1
21	26	+	12	4
22	32	+
23	37	+
24	42	+

6. Проводится расчет параметров сравнения ν = 12 и τ_иакс= 4 , а также сравнение рассчитанных значений с теоретическим, ν_p и табличным (критическим) τ_о. Для расчета теоретического значения ν_p используется следующее выражение их (2.2)

ν_р = [(1/3)(2n - 1) - 1,96* ]. (2.3)

Подставляя в (2.3) значения, получаем, для n = 24

ν_р = [11,774] = 11.

По таблице (2.1) определяем критическое значение τ_o = 6.

Проводим сравнение параметров ν и τ с критическими значениями по решающему правилу (2.2)

ν = 12 > ν_р = 11, - условие удовлетворяется,

τ_иакс = 4 ≤ τ_o = 6 - условие удовлетворяется. (2.4)

Применяя правило (2.2) - если нарушается хотя бы одно из вышеприведенных неравенств (2.4), то гипотеза об отсутствии тренда отвергается. Таким образом, если оба условия выполняются, то тренда нет.

Вывод. Так как оба условия выполняются, то тренд в исследуемом ряду динамики отсутствует.