6. Методы и модели аналитического выравнивания

6.1.Аппроксимация временных рядов аналитическими функциями

Как уже отмечено выше, одной из важнейших задач иссле­дования экономического временного ряда является выявление основной тенденции изучаемого процесса, выраженной неслучай­ной составляющей (тренда либо тренда с циклической или (и) сезонной компонентой).

Для решения задач такого типа, связанных с анализом данных при наличии периодических и случайных воздействий, используется инструментарий анализа, базирующийся на использовании кривых (криволинейных функций) роста. Этот инструментарий используется не только для анализа и моделирования систематических долговременных составляющих временного ряда, но и для проведения интерполяции и экстраполяции исследуемого процесса. Таким образом, эти методы позволяют выявлять закономерности на фоне случайностей, делать обоснованные прогнозы и оценивать их достоверность и вероятность их выполнения.

Такой инструментарий представляет собой методы экономико-математического моделирования, основанные на построении модели экономического процесса, позволяющей установить количественные зависимости между параметрами исследуемого явления. Такая модель, в основном, строится на базе методологии регрессионного анализа и позволяет выявить форму, вид связи и силу влияния факторных признаков, отражающих исследуемый процесс, на результативный показатель. При этом, возможно определение вида связи, отражающей тенденцию изменения результативного признака под воздействием исходного факторного показателя, включающего как один исходный показатель, так и несколько.

Наибольшее распространение получили модели, представляющие собой регрессионные уравнения связи между различными факторами, влияющими на развитие рассматриваемого экономического процесса [1,3,6,9]. Одной из задач, возникающих при анализе рядов динамики, является установление закономерности изменения уровней изучаемого показателя во времени, где сами закономерности могут быть описаны аналитическими функциями времени.

Для этого, уровень изучаемого показателя оценивается как функция времени

,

где - уровни динамического ряда.

Такой способ сглаживания ряда является наиболее распространенным и позволяет получить выровненные (теоретические) значения уровней ряда. Как ранее было сказано, для аналитического выравнивания используются три типа функций: - монотонные, - с насыщением и разными значениями темпов роста, - с насыщением и точкой перегиба. Все эти функции отражают различные по содержанию экономические процессы и требуют адекватного выбора кривой отражающей смысл развития процесса.

Среди множества функций времени, наибольшее значение имеют более простые функции, в виде полиномов с параметром времени.

Среди таких функций есть простые полиномы, или линейные функции вида

y_t = а₀ + а₁t,

параболические функции вида

y_t =a_o+ a₁t+ a₂t²,

гиперболические функции вида

y_t = a_o + a₁t + a₂t² + a₃t³

общий вид полинома

и другие виды функций времени, например, экспоненциальные, логарифмические, степенные, показательные, логистические и пр.

Рассмотрим подробнее характеристики отдельных типов функций времени, наиболее часто применяемых в практике эконометрического моделирования. В общем виде, группа полиномиальных функций может быть описана следующим выражением (полиномом):

, (6.1.)

где: a_j (i = 1,... ,n) - параметры многочлена, t - независимая переменная (время).

Коэффициенты полиномов невысоких степеней могут иметь кон­кретную интерпретацию в зависимости от содержания динамического ря­да. Обычно в экономических исследованиях применяются полиномы не выше третьего порядка. Использовать для определения тренда полиномы высо­ких степеней возможно использовать только при интерполяции, для прогнозирования, их применение нецелесообразно, поскольку полученные таким образом ап­проксимирующие функции будут отражать случайные отклонения в прошедшем периоде.

Полином первой степени y_t = a_o+a₁t на графике изображается прямой и используется для описания процессов, развивающихся во времени рав­номерно.

Полином второй степени y_t =a_o+a₁t+a₂t² применим в тех случаях, ко­гда процесс развивается равноускоренно (т.е. имеется равноускоренный рост или равноускоренное снижение уровней).

Полином третьей степени имеет вид y_t = a_o + a₁t + a₂t² + a₃t³. Отличительная черта полиномов - отсутствие в явном виде зависи­мости приростов от значений ординат (y_t).

Для сглаживания временных рядов наиболее часто применяются функции прямой. параболы, экспоненты, логарифмической параболы и др. Параметры таких функций имеют качественный экономический смысл и легко интерпретируются.

При выборе соответствующей функции y_t используют содержательный ана­лиз (который может установить характер динамики процесса), визуальные наблюдения (на основе графического изображения временного ряда). При выборе полиномиальной функции может быть применен метод последовательных разностей (состоящий в вычислении разностей первого порядка , второго порядка и т.д.), и порядок разностей, при кото­ром они будут примерно одинаковыми, принимается за степень полинома.

Из двух функций предпочтение обычно отдается той, при которой меньше сумма квадратов отклонений фактических дан­ных от расчетных на основе этих функций. Но этот принцип нельзя доводить до абсурда: так, для любого ряда из n точек можно подобрать полином ( )-й степени, проходящий через все точки, и соответственно с минимальной — нулевой — сум­мой квадратов отклонений, но в этом случае, очевидно, не сле­дует говорить о выделении основной тенденции, учитывая слу­чайный характер этих точек. Поэтому при прочих равных усло­виях предпочтение следует отдавать более простым функциям.

Теоретически искомая функция тренда может определяться из достаточно широкого класса функций. Однако на практике ее нахождение обуславливается рядом факторов. Выбранная функция тренда должна удовлетворять следующим основным условиям:

1) быть теоретически (с точки зрения экономической теории) обоснованной,

2) содержать минимальное число влияющих факторов,

3) параметры ее должны иметь конкретное экономическое содержание

4) расчетные значения тренда должны как можно меньше отличаться в своей совокупности от соответствующих фактических наблюдений временного ряда.

Для выявления основной тенденции чаще всего используется метод наименьших квадратов, т.е. оценка параметров уравнения сглаживания (функции времени), обычно, осуществляется на базе метода наименьших квадратов (МНК). Суть его состоит в отыскании таких параметров уравнения тренда, при которых сумма квадратов отклонений расчетных уровней тренда от их фактических значений ( y_t - y(t)) ² , ( t = 1, 2, . . . , n), была бы минимальной, т. е. решается задача минимизации критерия отклонения:

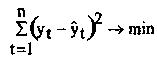(6.2)

где y_t - фактическое значение временного ряда; у(t) - расчетное значение;

п - длина временного ряда.

Кратко, суть математического аппарата метода наи­меньших квадратов, подробно описанного в литературе [1,4] и включает следующие процедуры.

На практике подбор вида функции тренда, параметры которой определяются по МНК, производится в большинстве случаев эмпирически, путем сравнения их между собой по величине среднеквадратического отклонения.

Описание методологии получения системы уравнений в общем виде, для полинома (6.1) предполагает получение системы нормальных уравнений, по минимизации выражения (6.2.), вида:

(6.3)

Система (6.3.) состоит из (n + 1) уравнений, содержащих в качестве неизвестных величин (n + 1) коэффициентов а_о, а₁ ... , а_n . Решение этой системы позволяет вычислить оценки искомых коэффициентов.

Рассмотрим выравнивание ряда динамики линейной функцией, т.е. аналитическим уравнением вида

, где t - порядковый номер периода.

В соответствии с МНК, параметры линейной функции времени рассчитываются на основании получаемых по данному методу системы нормальных уравнений. В данном случае, для линейной функции система уравнений имеет вид:

(6.4)

Решая данную систему одним их нескольких способов решения, получаем значения параметров линейной функции (коэффициентов уравнения) .

Решение этой системы относительно искомых параметров дает следующие выражения

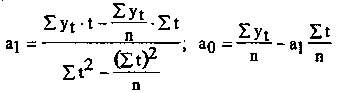(6.5)

Учитывая, что значения переменной образуют натуральный ряд чисел от 1 до , суммы можно выразить через число членов ряда по известным в математике формулам:

. (6.6)

По рассчитанным параметрам записываем уравнение аппроскимирующей линейной функции для исследуемого динамики : .

Для параболы 2-го порядка получим аналогичную систему нор­мальных уравнений:

(6.7)

Эта система содержит три уравнения, позволяющих найти оценки трех неизвестных коэффициентов а_о, a₁, а₂.

Составление нормальных уравнений можно упростить, воспользо­вавшись тем, что величины ... не зависят от конкретных уров­ней динамического ряда. Эти суммы являются функциями только числа членов в динамическом ряду. Для них получены следующие формулы:

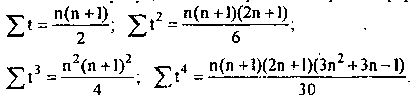
(Суммирование по t = 1 - n).

Другой подход к упрощению расчетов параметров уравнения заключается в переносе на­чала координат в середину ряда динамики. Это позволяет упростить сами нормальные уравнения, а также уменьшить абсолютные значения величин, участвующих в расчете. Если до переноса начала координат t было равно 1,2,3,...,n то после переноса:

для четного числа членов ряда t =...,-5;-3;-l;l;3;5;...,

для нечетного числа членов ряда t =...,-3;-2;-l;0;l;2;3;... .

Таким образом, , где k - нечетное число, равна 0. Такой под­ход существенно упрощает систему(6.4), и тем более (6.7).

В этом случае оценки параметров соответствующих полиномов имеют вид:

прямой

(6.8.)

параболы

,

, (6.9)

.

Для класса экспоненциальных кривых, в отличие от полиномов, ха­рактерной является зависимость приростов от величины самой функции. Эти кривые хорошо описывают процессы, имеющие "лавинообразный" характер, когда прирост зависит от достигнутого уровня функции.

Простая экспоненциальная (показательная) кривая имеет вид:

(6.10)

Если b > 1, то кривая растет вместе с ростом t, и падает, если b < 1.

Параметр а характеризует начальные условия развития, а параметр b - постоянный темп роста.

Действительно, темп роста равен

В данном случае

Соответственно и темпы прироста постоянны.

Можно показать, что логарифм ординаты этой функции линейно зависит от t, для этого прологарифмируем выражение (6.10):

Пусть log a = A; log b = B. Тогда log y_t =A + t*B.

Теперь для оценивания неизвестных параметров можем использо­вать систему нормальных уравнений для прямой (6.4.).

В этом случае критерий отклонения имеет вид:

Иначе говоря, нормальные уравнения строятся исходя из миними­зации логарифмических выражений. Соответственно в нормальных уравнениях вместо фактических уровней выступают их логарифмы:

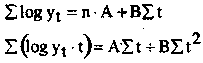(6.11)

Нахождение неизвестных параметров А и В проводят исходя из значений A = log а и В = log b. Отсюда, параметры а и b определяют с помощью потенцирования и получают показательную функцию, служащую для выравнивания ряда. Однако, полученные оценки параметров оказываются смещенными, т. к. при расчете участвуют не исходные уровни, а их логарифмы. Смещение будет тем значительнее, чем больше разность между последовательными уровнями динамического ряда. Для снижения уровня ошибки (смещения) используют нелинейный метод наименьших квадратов.

Более сложным вариантом экспоненциальной кривой является ло­гарифмическая парабола

(6.12.)

Прологарифмировав выражение (6.12), получим параболу

Таким образом, оценку параметров логарифмической параболы можно также осуществить с помощью метода наименьших квадратов, ис­пользуя систему нормальных уравнений для параболы (6.7), но с учетом возможного смещения оценок параметров.

Все рассмотренные типы кривых используются для описания моно­тонно возрастающих или убывающих процессов без "насыщения".

Когда процесс характеризуется "насыщением", его следует описы­вать при помощи кривой, имеющей отличную от нуля асимптоту. Приме­ром такой кривой может служить модифицированная экспонента:

_, (6.13)

где у = k является горизонтальной асимптотой.

При заданных значениях асимптоты k, другие параметры кривой могут быть определены с помощью метода наименьших квадратов после приведения уравнения к линейному виду:

(6.14)

где k— заданное значение асимптоты

Если прологарифмировать (6.14):, получим следующее выражение

Теперь оценить параметры log а и log b можно, используя систе­му нормальных уравнений (6.11).

Для оценивания параметров модифицированной экспоненты воз­можно применение как нелинейного метода наименьших квадратов, так и ряда других методов, в которых вычисления проще, но оценки менее эф­фективные.