4. Модель динамического ряда с аддитивными компонентами

4.1. Оценка сезонной компоненты в аддитивных моделях

Пусть наш исследуемый ряд, состоящий из квартальных объемов продаж, имеет динамику, которая характеризует аддитивную модель временного ряда. Т.е. фактически объемы продаж можно выразить следующим образом:

A = T + S + E. (4.1)

Для выделения сезонной компоненты из ряда А (4.1) и ее исследования, можно использовать метод скользящей средней. Динамика продаж представлена в табл.4.1.

Таблица 4.1. Динамика продаж

Год	Период (квартал)	Объем продаж, тыс. шт.	Год	Период (квартал)	Объем продаж, тыс. шт.
		А			А
2005	1	239	2007	9	401
	2	201		10	360
	3	182		11	335
	4	297		12	462
2006	5	324	2008	13	481
	6	278
	7	257
	8	384

Исходные поквартальные данные можно изобразить графически (рис.4.1)

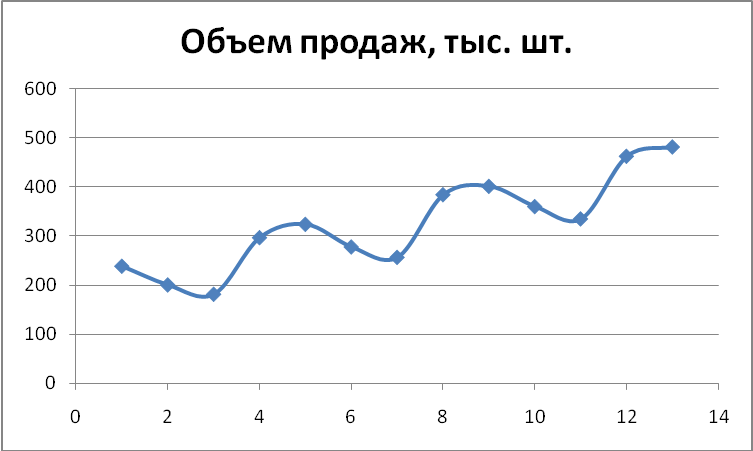
Рисунок 4.1. Аддитивная модель ряда продаж

Для выделения тенденции в ряду воспользуемся метом скользящего среднего. Для этого возьмем в качестве интервала сглаживания количество периодов, равных кварталу, т.е. m=3. Причем, среднеквартальный объем продаж уже не содержит сезонной компоненты, поскольку пред­ставляет собой среднюю величину в пределах года.

Каждая величина средней характеризует оценку значения тренда для середины сглаживаемого периода. Таким образом получаем множество скользящих средних, которые характеризуют более лучшую, выровненную динамику процесса, который позволяет определить тренд в ряду динамики. Матрица расчета скользящего среднего для диапазонов сглаживания m = 3 и m = 4 приведена в табл.4.2. Полученные тренды скользящих средних показаны на рис.4.2

Таблица 4.2. Расчет скользящих средних (квартальных)

Период	Объем продаж, тыс. шт.	сглаженные данные, m=3	сглаженные данные, m=4
1	239
2	201
3	182	207,33
4	297	226,67	229,75
5	324	267,67	251
6	278	299,67	270,25
7	257	286,33	289
8	384	306,33	310,75
9	401	347,33	330
10	360	381,67	350,5
11	335	365,33	370
12	462	385,67	389,5
13	481	426,00	409,5

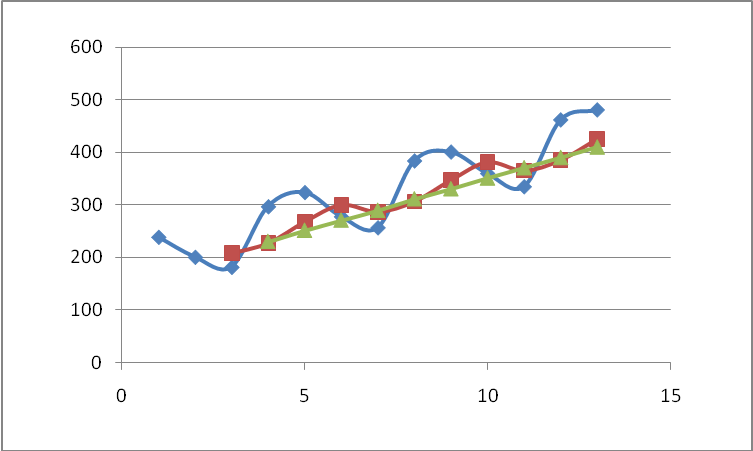
Рисунок 4.2. Тренды скользящих средних при m = 3 и m = 4

Оценка скользящего тренда при m = 4 показывает более плавную и линейную тенденцию.

Теперь полученные значения тренда можно использовать для нахождения оценок сезонной компоненты. Из (1) можно получить модель уровня ряда в таком виде модели

А – T = S + E. (4.2)

Для дальнейших расчетов тренда, необходимо найти десезонализированные (скользящие) средние значения, соответствующие тем же ин­тервалам времени, что и фактические значения за квартал. Но, оценки значений тренда, полученные в результате расчета скользящих средних относятся к несколько иным моментам времени, чем фактические данные. Для анализа же требуются десезонализированные средние значения, соответствующие тем же ин­тервалам времени, что и фактические значения за квартал. Для выравнивания данных необходимо сдвинуть положение десезонализированных средних во времени путем дальнейшего расчета средних для каждой пары значений рядом стоящих уровней.

Средняя для первой пары полученных средних получается в виде

(229,75 + 251) / 2 = 240,4.

Это значение называется десезонализированной средней, которую еще называют центрированной скользящей средней. Именно такие значения уже можно сравнивать с фактическими значением.

Результаты расчетов центрированной скользящей средней приведены в табл. 4.3. Электронная таблица расчета показана на рис.4.3.

Таблица 4.3. Расчет центрированных скользящих

средних значений тренда для модели А – Т = S + Е

Период	Объем продаж, тыс. шт.	Сглаженные данные, m=4	Центрированные скользящие средние	Оценка сезонной компоненты
	А		Т	A – T = S + Е
1	239
2	201	229,75
3	182	251,00	240,38	-58,38
4	297	270,25	260,63	36,38
5	324	289,00	279,63	44,38
6	278	310,75	299,88	-21,88
7	257	330,00	320,38	-63,38
8	384	350,50	340,25	43,75
9	401	370,00	360,25	40,75
10	360	389,50	379,75	-19,75
11	335	409,50	399,50	-64,50
12	462
13	481

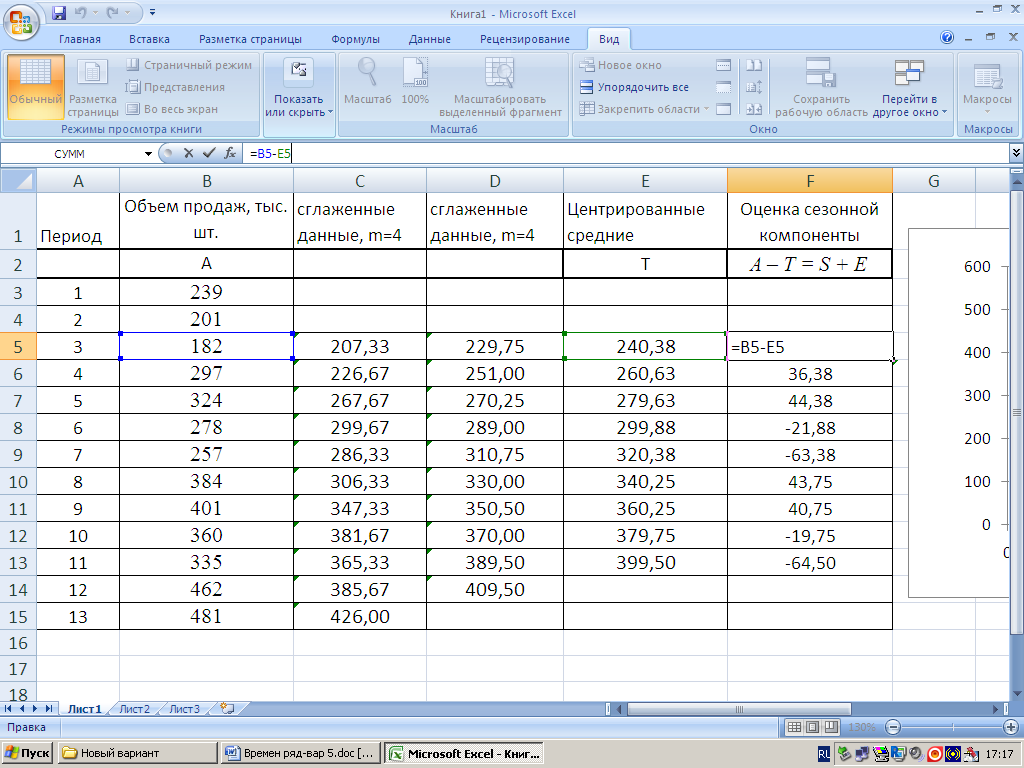
Рисунок 4.3. ЭТ расчета центрированных скользящих средних

По результатам расчета, имеются оценки сезонной компоненты, которые вклю­чают в себя ошибку (остаток).

Далее необходимо найти средние значения сезонных оценок для каждого сезона года, что снизит влияние ошибки. А далее следует скорректировать средние значения. Корректировка состоит в увеличении или уменьшении средних значений на одно и то же число (корректирующий фактор) таким образом, чтобы общая их сумма была равна нулю. Это необходимо для усреднения значения сезонной компонен­ты в целом за весь период наблюдения. При этом выбираются одинаковые кварталы за разные годовые периоды.

Корректирующий фактор рассчитывается следующим образом: сумма оценок сезонных компонент делится на 4. Распределение данных по кварталам приведено как показано в табл.4.1, поэтому необходимо систематизировать одинаковые кварталы. Расчет средних значений сезонной компоненты приведен в табл.4.4.

Таблица 4.4. Расчет средних значений сезонной компоненты

Расчетный показатель	Год	Номер квартала
		1	2	3	4
	2005	–	–	-58,4	36,4
	2006	44,4	-21,9	-63,4	43,8
	2007	40,8	-19,8	-64,5	–
Итого		85,2	-41,7	-186,3	80,2
Оценка сезонной компоненты (средн)		42,60	-20,85	-62,10	40,10	Сумма =		- 0,25
Скорректированная сезонная компонента		42,60	-20,70	-62,00	40,10	Сумма =		0

Корректировка оценки сезонной компоненты заключается в изменении их значений таким образом, чтобы при равномерном положительном и отрицательном изменении, общая сумма была равна нулю.

Электронная таблица расчета приведена на рис. 4.4. Алгоритм расчета представлен на рис. 4.5.

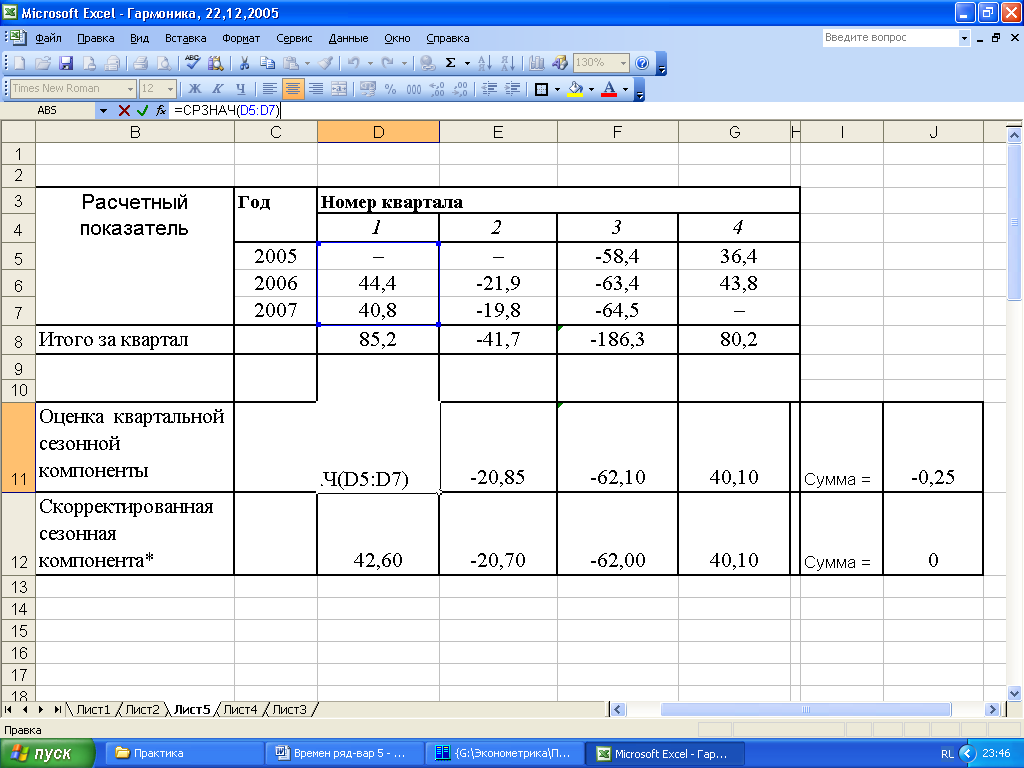
Рисунок 4.4. Электронная таблица расчета скорректированной сезонной компоненты

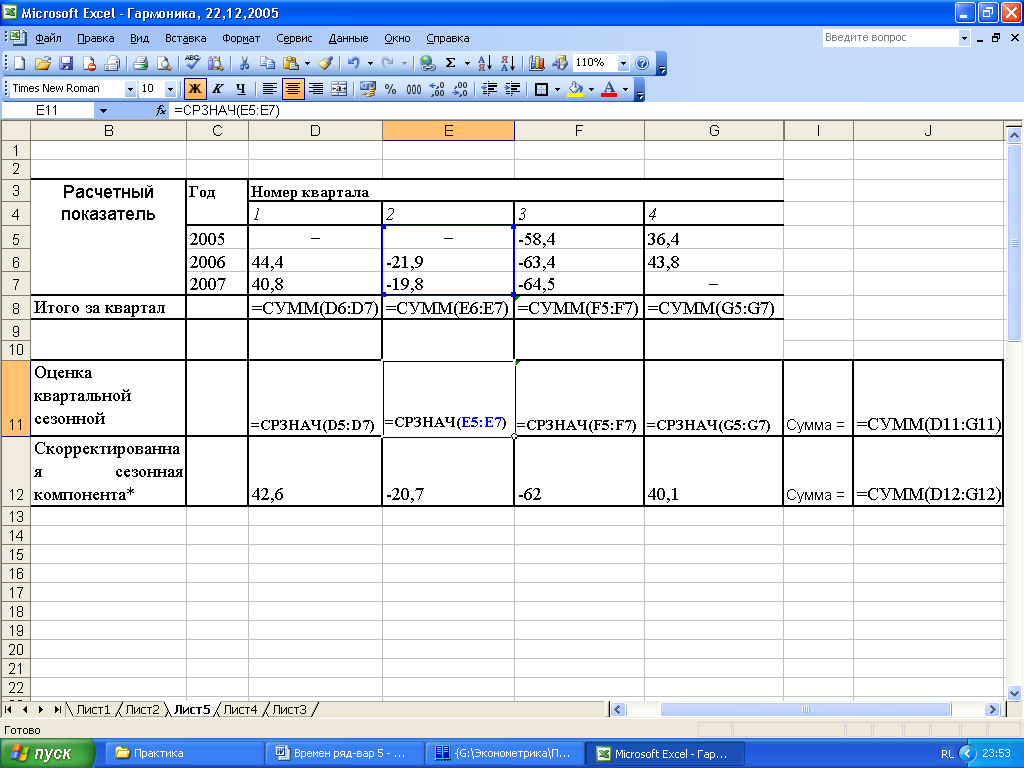
Рисунок 4.5. Алгоритм расчета сезонной скорректированной компоненты

Полученные значений сезонной компоненты позволяют сделать выводы о том, что объемы продаж за два зимних квартала превы­шают среднее трендовое значение приблизительно на 40 тыс. шт., а объемы продаж за два летних периода ниже средних примерно на 20 и 60 тыс. шт. соответственно.

Такая процедура выявления сезонной компоненты применима при определении сезонной вариации за любой промежуток времени, только период сглаживания берется адекватный промежутку времени. Если, например, в качестве сезонов выступают дни недели, то оценки влияния ежедневных колебаний рассчитывают скользящую среднюю взятую в пределах недели, т.е. период сглаживания m = 7. Эта скользящая средняя представляет собой значение тренда в середине недели и необходимость в процедуре центрирования отпадает.