3. Попереднє дослідження
У [12] автори ініціюють задачу виявлення схеми відновлення, яка може гарантувати оптимальне поширення навантаження найгіршого випадку, коли більшість k комп'ютерів вимикаються. Схеми повинні мати такий великий k як можливо. Автори представляють і доводять в Log алгоритм, це робить схема відновлення, яка гарантує оптимальність, де найбільше log2n комп'ютерів вимкнено. Оптимальний засіб, коли максимальне число процесів на тому ж комп'ютері після k вимкнень − MV(k), де функція MV(k) забезпечує нижню межу для будь-якої схеми статичного відновлення. Функція MV описується пізніше у Секції 4.1.
Інший алгоритм, під назвою Ощадливий, представляється в [11]. Цей алгоритм генерує схеми відновлення, які дають оптимальність для більшого ряду випадків, ніж алгоритм Log (тобто. Ощадливий дає гарантії оптимальністі також, коли більш ніж log2n комп'ютерів вимкнені.). Ощадливий алгоритм заснований на математичній задачі виявлення послідовністі додатніх цілих чисел таких, що уся сума послідовностей унікальна і мінімальна.
Це просто, для того щоб вичислити Ощадливий алгоритм навіть для великого n. Список відновлень для процесу нуль, виконуючись на комп'ютері нуль, складається з двох частин. Перша частина − послідовність від ощадливого алгоритму, і з другою частиною заповненою номерами, що залишилися. Інші списки із самого початку, включають єдиний сенс (як описано в Секції 2 в цій статті) модуля. Схема відновлення складається з усіх списків відновлень. Окремий випадок Ощадливого алгоритму − алгоритм під назвою Голомбо, описав [9]. Ім'я цього алгоритму походить від лінійки Голомбо, яка є послідовністю додатніх цілих чисел таких, що немає двох чітких пар, номери від множини мають ту ж різницю. Ці номери − названі позначками і відповідають позиціям на лінійному масштабі. Різниця між значеннями яких-небудь двох позначок названа відстанню. Найкоротша лінійка Голомбо для цього ряду позначок названа Оптимальною Лінійкою (OGRs) Голомбо[3]. Пошук Оптимальної Лінійки Голомбо стає важчим, оскільки число позначок зростає. Це відомо як NP−complete задача [16]. Задача виявлення OGRs для великого ряду позначок є ще невирішеною. Приклад представлення OGR з чотирма позначками показується в Мал. 2. Можливо виміряти відстані: 1; 2; 3; 4 як 1+3; 5; 7 як 5+2; 8 як 3+5; 9, як 1+3+5; 10 як 3+5+2 і 11 як 1+3+5+2, але ми не можемо виміряти відстань 6.
Мал. 2 представлення лінійки Голомбо для чотирьох позначок
Лінійки Голомбо можуть також бути представлені як трикутник, де кожен номер представляє різницю між парою специфіки номерів. Мал. 3 показує приклад з чотирма позначками (такий же приклад, як в Мал. 2).
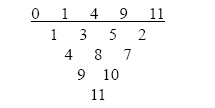
Мал. 3 Трикутне представлення лінійки Голомбо
У лінійки Голомбо циклічні переходи проігноровані, тобто ситуації, коли підсумок числа "стрибків" для процесу більше, ніж число комп'ютерів в кластері. ("стрибок" − відстань між пошкодженим вузлом і вузлом, на якому процес треба бути знову почати). У тому числі циклічні переходи дають нове математичне формулювання з виявленням щонайдовшої послідовності додатніх цілих чисел таких, що сума і суми з усього модуля послідовностей (у тому числі послідовності довжини один) n унікальні (для цьго n). Це математичне формулювання комп'ютерної постановочній задачі дає нові потужніші схеми відновлення, звані Модульними схемами, для о більшого числа пошкоджених комп'ютерів, ніж схеми [Голомбо 10].
Усі ці алгоритми (Log, Ощадливий, Голомбо і Модуль) гарантують оптимальність певного числа пошкоджених комп'ютерів в кластері. У [8] ми обчислюємо кращі можливі схеми відновлення для будь-якого числа пошкоджених комп'ютерів. Через обчислювальну складність задачі, знахідки, такої схеми відновлення − комплексна задача. Ми тільки можемо подати оптимальну схему відновлення для максимуму 21 комп'ютера у кластері (n ≤ 21 ).
Тут ми подали нові схеми відновлення, які засновані на Оптимальних Лінійких Голомбо і гарантують оптимальну поведінку для набагато більшого ряду пошкоджених вузлів.