2 Багатопроцесорне Планування (Частина I)

У цій секції ми представляємо класифікацію планування проблем і присутню роботу, пов'язану з межами і складностями для деяких з них.

Дуже хороша таксономія завдання планування в розподілених системах обчислення представлена в

Casavant і Kuhl в [8] (подивіться Мал. 2). Тут, статичні засоби недоступні, тобто, рішення для процесу зроблене перед тим, як воно виконуватиметься, при динамічних засобах он-лайн, тобто, коли невідомо, коли і де процес виконуватиметься впродовж його тривалості життя. У Статті1 і 2 ми розглядаємо глобальне оптимальне статичне планування, коли ми знаємо інформацію з паралельної програми заздалегідь.

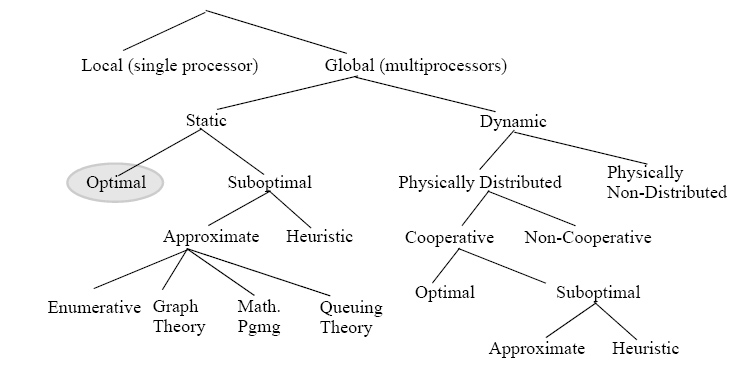
2.1 Класифікація планування проблем

Ми починаємо з визначення планування, що розвивається по схемі Graham, Lawler, Lenstra і

Rinnooy Kan [28]:

Розглядаємо машини м Mi (i = 1,...,m) яким треба обробити n роботи Jj (j = 1,...,n).

Графік - розміщення одного або більше інтервалів часу на одній або більше машинах для кожної роботи. Графік виконується, якщо два інтервали часу розподілили для того ж робочого перекриття, і якщо, крім того, це відповідає ряду специфічних вимог з приводу машинного середовища і робочих характеристик. Графік оптимальний, якщо це мінімізує критерій оптимальності.

До того ж, автори (Graham і інший. [28]) запропонували класифікацію планування

проблеми, яка була широко використаниа в літературі, наприклад Lawler і інший. [38], Blazewicz і інший. [4], Pinedo [55]. Класифікація показує, скільки проблем в плануванні теорії може бути, якщо б ми подивилися на усі комбінації. Ця дисертація обмежена одним типом машин і в одному критерії, тобто мінімальному часі завершення. Класифікація планування проблеми представляється як трипільна класифікація , де представляє середовище процесора, робочі характеристики і критерій оптималності як зазначено нижче:

Перше поле α = α₁α₂ складається з двох параметрів: α₁ ∈{°,P,Q,R,O,F,J} де (означає порожній символ) представляє єдиний процесор; P: ідентичні процесори; Q: однорідні процесори, тобто процесори з цією швидкістю; R: unrelated процесори тобто процесори із залежними для роботи швидкостями; O: виділяємо процесори: відкрите з цехове встановлення послідовності, в якому кожну роботу доведеться обробити знову на кожному одному з м процесорів; немає ніяких обмежень відносно замовлення кожної роботи; F: виділяємо процесори: відкрите цехове встановлення послідовності, в якому кожну роботу доведеться обробити на кожному одному з процесори м із спеціальним замовленням, тобто спочатку на процесі один, потім на процесі два і так далі. Після завершення на одному процесорі, робота приєднується до черги в наступному процесорі; J: виділяємо процесори: встановлюємо послідовності роботи обчислювального центру, кожна робота має свій власний наказ слідувати; і: число процесорів (Pinedo, [55])

У Статті 1 ми описуємо сценарій ідентичних машин з різним числом процесорів, тобто множина Pk для паралельної архітектури з k ідентичними процесорами і статичний розподіл, і множина Pq - з q ідентичними процесорами і динамічним розподілом.

Потім . В Статті2 , тут ми також описуємо сценарій ідентичних машин з процесорами м. Друге поле описує робочі характеристики. Тут ми описуємо тільки щось з можливих значень β ∈{°, pmtn,prec, tree,res, rj, pj = 1}., де йде на увазі, що це немає ніяких обмежень на роботи; pmtn означає, що пріоритетні переривання дозволяються; prec є перевагою відношення між роботами, дерево - деревне представлення, що вкорінилося; ре вказане обмеження ресурсу; rj - дата вручення; pj = 1: кожна робота має одиничну обробку вимоги (відбувається, тільки якщо α ∈{°,P,Q}).

У Статті 1 ми не маємо ніяких робочих характеристик, так для обох випадків (Pk і Pq)

У Статті 2 , ми відобразили сценарій з обмеженим числом пріоритетних переривань, тобто, останнє поле описує критерій оптимальності. Зазвичай вибраним найбільшим є час максимального завершення або робочий інтервал (Cmax), повний час (ΣCj ) завершення чи максимальне запізнення Lmax, де запізнення завдання - його час завершення крайній термін [Graham і інший., 28].\

У Статті1 і 2 ми зацікавлені в зменшенні робочого інтервалу, тобто для мінімізації часу максимального завершення, тобо γ = Cmax .

Користуючись цим відображенням, ми можемо представити проблему зменшення максимального завершення часу на ідентичних паралельних машинах, що дозволяють пріоритетне переривання, як P pmtn Cmax .