4.2 Продовження процесів
Це перетворення істотне для спрощення у безлічі "більш погано працюючих" які ми називаємо «завершеними» . Ми бачитимемо, що властивість опуклості перетворення (Теорема 1:) грає центральну роль.
Ми перетворюємо програму Р в Р’ продовженням процесів. Тобто, ми пропонуємо кожного разу доки x, x > 0, з кожного процесу в програмі Р таким чином Δx, що Δ(x⁄x) - те ж для усіх процесів. Програма Р’
потім перетворена в Р’’ таким же чином. Тобто, після перетворення кожного разу коли блок x + Δx продовжено на Δx . Кожну Роботу(x) замінює Робота (x+ Δx) для Р’ і константа Роботи (x + 2Δx) для Р’’
, де Δ(x⁄x) .
Це перетворення не впливає на синхронізацію. В цьому випадку динамічного розподілу, коли вартість синхронізації дорівнює нулю після продовження, ми просто маємо:
.
Ситуація для статичного розподілу відмінна від попередньої. Починаючи з вартості комунікації, яка в цьому випадку не нульова, відмінності після продовження не завжди зберігаються, тому що ми не продовжуємо синхронізацію. Мал. 5 демонструє перетворення. Для простоти зображення знаками ми позначаємо час Ts(P,A) статичного завершення замість Ts(P, A, k, t), і позначаємо довжину програми L minA = Ts(P,A) . різницею між Р і Р’ позначаємо, як ΔL . Це означає, що довжина програми Р’ дорівнює L′ = L + ΔL Програма Р’’ створюється так само, використовуючи те ж Δx в Р’ .
Різниця між Р’ і Р’’ ми позначаємо, як ΔL’. Потім довжина програми Р’’ буде L″ =(L + ΔL)+ ΔL′.
Рис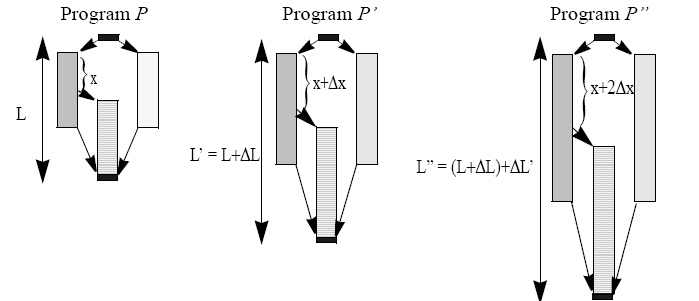
Рис 5. Перетворення програми Р за допомогою пролонгації
Властивість опуклості, яка формулюється в Теоремі 2, витікає з Теореми 1 і заявляє, що ΔL ≤ ΔL′ . Ці теореми визначаються пізніше. Для того, щоб обговорювати ефект роздільного локального планування, ми розглянемо тільки один процес на процесор. Ми ослабимо це обмеження у кінці цього розділу.
Спершу ми визначаємо деяку термінологію:
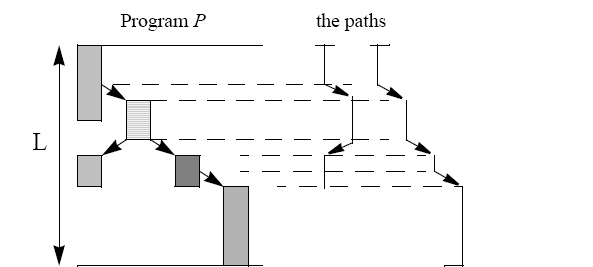
Шляхом програми ми визначаємо підключену послідовність сегментів і синхронізації сигнали. Шлях починається завжди на початку програми. Довжиною шляху ми визначаємо час для усього виконання і сигналів синхронізації, які включаються у шлях. Найдовшим шляхом ми визначаємо шлях з максимальною довжиною. Критичним шляхом ми визначаємо щонайдовший шлях з мінімальним числом сигналів синхронізації. Отже коли ми маємо два щонайдовші шляхи, потім критичний шлях буде шляхом з менше стрілки. Для простоти ми використовуємо "стрілку" це скорочення для поняття «синхронізаційний синал»
Мал. 6 показує програму з чотирма процесами на чотирьох комп'ютерах, що містять чотири синхронізаційні сигнали. Права частина малюнка показує ієрархічну структуру двох шляхів. шлях лівої сторони складається з трьох сегментів і двох стрілок, при праві один, це довше складається з чотирьох сегментів і трьох стрілок. Довший є звичайно критичний шлях.
Рис 6, Графічне відображення програми Р і її «шляхи», критичний шлях є найдовшим стр(P) = 3.
Можливо, що критичний шлях не має ніяких стрілок. У такому разі, критичний шлях складається
тільки з одного процесу. Також можливо, що критичний шлях змінює свій шлях, коли ми просуваємося to P P′ або від, to P′ P″ і в наслідок чого число стрілок може змінватись. Як згадуваолсь раніше ми завжди переймаємо на себе оптимальне локальне планування. Спершу ми показуємо, що для продовження число стрілок в критичному шляху не може зростати.
Нехай стр(P) є числом стрілок в критичному шляху програми Р, і дозволяє стр(P ″) бути числом стрілок в критичному шляху програми Р’ (тобто Р після продовження).
Лема 2: . стр(P) ≥ стр(P′)
Доказ: Припускають, що стр(P) = m,(m≥ 0) і що в програмі Р є інший шлях, що складається із кількості стрілок М. Коли ми продовжуємо процеси, шлях з більшими стрілками обов'язково має менше виконання. Потім цей шлях зростає повільніше, ніж критичний шлях. Тому, шлях із більшою кількістью стрілок не може бути критичим .
Отже: стр(P) ≥ стр(P′).
Рис. 7 показує ієрархічну структуру перетворення із статичним розподілом. Програма Р складається з двох шляхів: перший з двома сегментами і одним сигналом синхронізації, і другий шлях з трьома сегментами і двома сигналами синхронізації. Другий шлях довший і це - критичний шлях. Впродовж перетворення перший шлях подовжується швидше і в наслідку це - критичний шлях в програмі P″ .
Розглядаємо, що в програмі Р’ обидва шляхи рівні. В цьому випадку перший шлях з коротшими сигналами синхронізації є
критичним шляхом. Рис показує також: стр(P)≥стр(P′) і ΔL ≤ ΔL′ .
Рис 7. Трансформація продовженням
Теорема 1: . ΔL ≤ ΔL′
Доказ: Нехай E1 = y1 + стр(E1) ⋅ t буде довжиною шляху один, де y1 – сума довжин сегментів (виконання) в шляху один, і стр(E1) - число стрілок де вартість комунікації = t. Нехай E2 = y2 + стр(E2) ⋅ t буте відповідати довжині шляху два. До того ж, припустимо, що y1 > y2 і що шлях два є критичним тобто: E1 < E2
Нехай E1′ = y1(x + Δx)⁄ x + стр(E1)t і E2′ = y2(x + Δx)⁄ x + стр(E2)t шляхи після першого продовження. І нехай тоді E1″ = y1(x + 2Δx)⁄ x + стр(E1)t і E2′ = y2(x + 2Δx)⁄ x + стр(E2)t
Будуть шляхами після другого продовження. Потім ми порівнюємо критичний шлях з будь-яким іншим шляхом протягом пролонгацій.
Є три можливі альтернативи:
(1)
Критичний шлях не змінює свою траєкторію, тобто E1 < E2 і E1' < E2' і E1'' < E2''
Тоді: ΔL=E2′ – E2
ΔL′=E2″ – E2′=E2′ – E2 = ΔL.
(2) критичний шлях змінює свій шлях після першого продовження
Тобто E1 < E2 E1' ≥ E2', і E1''>E2'' тоді ΔL < ΔL′ тому що шлях E1 росте швидше, ніж E2 .
(3) критичний шлях змінює свій шлях після другого продовження
тобто E1 < E2 E1' ≥ E2',і E1''>E2'' а потім ΔL < ΔL′, звичайно оскільки шлях E1 росте швидше, ніж E2 .
Тому, в усіх випадках ми маємо: ΔL ≤ ΔL′ .
Ми зараз беремо дві копії програми Р’ . З попередньої секції, тому що ми знаємо
що перетворення до м копій програми Р гарантує нам діапазон. Згідно з продовженням перетворення і Теоремою 1, ми маємо:
Теорема 2: 2L′ ≤L+L″ .
Доказ: 2L′=L + ΔL+L+ΔL ≤ L+ΔL+L+ΔL′=L+(L+ΔL+ΔL′) = L+L″.
Це означає, що довжина двох копій Р’ (після перетворення Р ) є меншою ніж відповідна сума довжин Р і Р’’ . Це властивість опуклості перетворення продовження.