3.3 Основні результати і план статті

Дані параметри n, k, q, t і z, ми характеризуватимемо як набір найгірше працюючих програм що матимуть назву «завершених». Ми робимо це починаючи з довільної програми і виконуючи послідовні перетворення. У кожному перетворенні програма стає "більш погано працюючою" в сенсі, що діапазон TS(P, k, t)⁄ Td(P,q) не зменшується.

Кінцевий результат - безліч завершених програм. Ці програми цілком мають таке . ж TS(P, k, t)⁄ Td(P,q) Відколи ми починаємося з довільної програми, ми враховуємо що програма є "більш погано працюючою» , відколи вони мають максимальний TS(P, k, t)⁄ Td(P,q) .

План статті представляється в Мал. 3. Ми починаємося з (Секції 4) з деяких перетворень

з однієї програми в копіях м цієї програми це дозволяє нам розбивати програму на дві частини. Перша частина складається з усього виконання, і описується в Секції 5. Друга частина, складається тількуи з синхронізації і, описується в Секції 6. У Секція 7 ми комбінуємо результати від цих частин в цілій програмі і тут є присутня формула для H(A, n, k, q, t, z) = g(A, n, k, q)+ zr(A, n, k, t) . Перша умова сума, що приходить з Секції 5, і другий з Секції 6. Формула H(n, k, q, t, z) = minAH(A, n, k, q, t, z)

зв'язує час завершення для будь-якої програми з n процесами, міра деталізації z і вартістю комунікації t наступною нерівністю .Ts(P, k, t)≤H(n, k, q, t, z)Td(P,q):

.

Тут . Ts(P, k, t) = minATs(P, k, t, A) у функції H(n, k, q, t, z)є оптимальною в розумінні, що щонайменше для деякої програми: : P Ts(P, k, t) = H(n, k, q, t, z)Td(P,q).

Тому, для усіх програм: : .

У Секції 7 ми подємо алгоритм «Гілок і меж» для ефективного обчислення H(n, k, q, t, z) H(A, n, k, q, t, z).

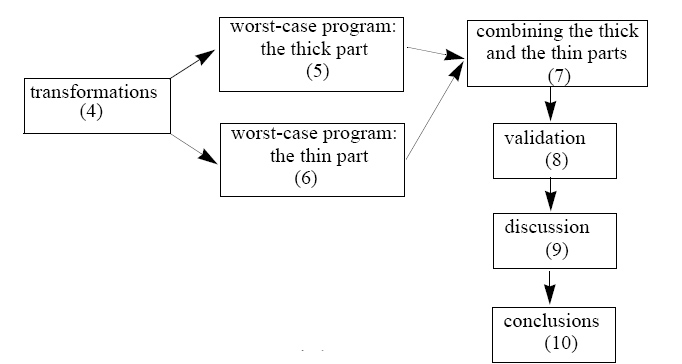
Рис. 3 – План статті

4 Перетворення програми р в нову програму що містить вузьку і широку частину.

У цій секції ми покажемо техніку, яка дозволяє нам перетворювати програму у нові програми, що складається з двох частин, одна це виконання (також називається товста частина), а інша частина тільки синхронізація (тонку частину). У цій секції ми показали дві леми і три теореми, що доводять можливість таких перетворень

4.1 Програма р’ як м-ідентична копія програми р

У цьому перетворенні ми конструюємо програму Р’, створюючи м копій програми Р

Усе виконання в копії x має бути завершене перед тим, як копія x+ 1 зможе початися. Це

не вимагає ніякої додаткової синхронізації, поки не буде необхідності в зв'язуванні процесів з добре визначеними точками початку і кінця (подивіться Мал. 4). У лемі 1 ми показуємо, що це перетворення не змінює коефіцієнт разів завершення з оптимальним статичним розподілом, порівнянним з оптимальним динамічним розподілом.

Лема 1: Діапазон часу завершення роботи при оптимальному часі завершення не розниться від переключення між програмами Р’ і Р

Доказ:, Маючи м (м > 1) копій програми Р, ми множимо обидві кількості

Рис. 4 показує перетворення програми в копіях м цієї програми позначається як Р’, Програма Р (ліва частина в малюнку) складається з виконання і синхронізаційних сигналів

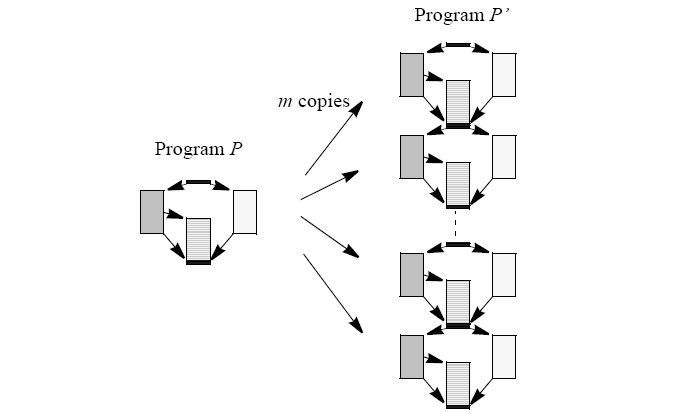
Рис 4. Перетворення програми Р м копій Р

Пізніше ми перетворимо ці м копій в двох частинах: одна частина з синхронізаційні

сигнали тільки один з повним виконанням. Перед цим, ми показували інше перетворення, перетворення -продовження, де ми продовжуємо процеси.