Теоретичні Аспекти на
Межі Продуктивності і Толерантність Дефекту
у Паралельних Обчисленнях
Kamilla Klonowska
Blekinge Інститут Докторських Серіїв Дисертації Технології
Немає 2007:18
ISSN 1653-2090
ISBN 978-91-7295-126-6
Теоретичні Аспекти на
Границі Продуктивності і Толерантність Дефекту в
Паралельних обчисленнях.
Kamilla Klonowska
Блекінжський технологічний інститут
Серія Докторських дисертацій
№ 2007:18
ISSN 1653-2090
ISBN 978-91-7295-126-6
Департамент по системам та прикладному програмному забезпеченню.
Школа розробки
Блекінжський технологічний інститут
ШВЕЦІЯ
© 2007 Камілла Клоновська
Департамент по системам та прикладному програмному забезпеченню
Школа розробки
Видавець: Блекінжський технологічний інститут
Надруковано: Друкарня Карлскрона, Швеція 2007
ISBN 978-91-7295-126-6
На згадку про мого Батька
Тадеуша Клоновскього
Дисертація представляється в Блекінжському Технологічному інституті на Технологічному факультеті для часткового задоволення вимог для отримання ступеня Доктора Філософії в Розробці Обчислювальних Систем.
Контактна інформація:
Камілла Клоновська
Департамент по системам та прикладному програмному забезпеченню
Школа Розробки, Блекінжський технологічний інститут
А/я 520
SE-372 25 Роннебі
Швеція
Електронна пошта: Kamilla.Klonowska@bth.se
Анотація
Ця дисертація складається з двох частин: Границі продуктивності для алгоритмів планування для паралельних програм в мультипроцессорних системах, і «Толерантність похибок» при схемах відновлення розподілених систем, коли один або більше комп'ютерів виходять з ладу (збоять).
У першій частині ми покажемо щільні межі в діапазоні для мінімального часу паралельного виконання программ на прикладі двох сценаріїв.
Сценарій №1 Діапазон мінімального часу завершення обчислення, коли процеси можуть бути перерозподілені у порівнянні із тим, коли вони не можуть бути перерозподілені до інших процесорів впродовж їх тривалості виконання.
Сценарій №2 Коли графік випереджуючий, а діапазон для мінімального часу завершення операції стоїть в межах, коли використовуються два різних типи переривань
Друга частина обговорює задачу перерозподілу навантаження серед запущених комп'ютерів в паралельній системі.
Мета - знайти схему перерозподілу, яка підтримує високу продуктивність навіть, коли один або більше комп'ютери йдуть з ладу . Тут ми показуємо чотири різні алгоритми перерозподілу навантаження.
У обох частинах ми використовуємо теоретичні техніки, що призводять до явно найгірше працюючих програм і сценаріїв. Коректність заснована на математичних доказах.
Підтвердження
Ця дисертація доктора філософії, можливо, ніколи б не зявилась без моїх наглядачів, колег, друзів і членів родини.
Спасибі. Я особливо дякую своїм наглядачам Професорові Ларсу Ландбергу і Доц. Хакану Лендерстаду за їх вклад в розділи, коментарі, ідеї, і заохочення впродовж цієї роботи;
Ларсу за його терпіння і Хакану за численні діалоги і обговорення проблем життя і математики.
Я також дякую членам моєї дослідницької групи : Чарлі Сванбергу за відповіді на усі мої питання і його вклад в Голомбо-series частинах, Девіту Менгісту за численні обговорення складності життя і планування, Саймону Канґстрону за допомогу мені у усвідомленні побудови/збірки, а також інших незрозумілих моментах, Пітер Троґеру за поглиблені обговорення про дефекти, помилки і збої, а такожі за підтримку моєї сім'ї впродовж останнього, найбільше напруженого вихідного, Мії Перссон за обговорення НП-складності, Ґорану Фріізу за те, що був моїм сусідом впродовж моїх звершень для досягнення ступеня Доктора філософії, Бенту Абсфаллу, Хакану Грану і Магнусу Бробергу, екс-члену цього докладу у першій частині.
Я також захотів би дякувати моїм колегам у департаменті, особливо Лінді Рамстерд
Джоанні Торнквіст, Лоренсу Геннесі, Дженні Люндберг, Ніні Дзамашвіллі - Фогельшторм, Гоха Баі, Маделіні Петерссон, Моніці Нільссон, Мей-Луїзі Андерссон, Петеру Нільссену.
Нарешті, я хочу принести мою вдячність до моєї сім'ї за їх підтримку і заохочення впродовж важких часів. Особливе спасибі до Яцеку і Віктору, моїй Мамі, тітці Вірі, Басі і тітці Льодзі, Івонці і Кжиштофу за те що вони були зі мною впродовж цього часу.
І моїм друзям: Радеку і Госі Шиманеку, Єві і Жонті Андерссон, Магдалені Урбанській, Віолі і
Томеку Маравчи, Каріні Стаховяк і Рафалу Ленці.
Список Літератури
Література що вклчена в цей доклад.
I “Comparing the Optimal Продуктивність of Parallel Architectures”
Kamilla Klonowska, Lars Lundberg, Hakan Lennerstad, Magnus Broberg
The Computer Journal, Vol. 47, No. 5, 2004
II “The Maximum Gain of Increasing the Number of Preemptions in
Multiprocessor Scheduling”
Kamilla Klonowska, Lars Lundberg, Hakan Lennerstad
submitted for publication
III “Using Голомбо Rulers for Optimal Recovery Schemes in Fault Tolerant
Distributed Computing”
Kamilla Klonowska, Lars Lundberg, Hakan Lennerstad
Proceedings of the 17th International Parallel & Distributed Processing Symposium
IPDPS 2003, Nice, France, April 2003
IV “Using Modulo Rulers for Optimal Recovery Schemes in Distributed
Computing”
Kamilla Klonowska, Lars Lundberg, Hakan Lennerstad, Charlie Svahnberg
Proceedings of the 10th International Symposium PRDC 2004, Papeete, Tahiti,
French Polynesia, March 2004
V “Extended Голомбо Rulers as the New Recovery Schemes in Distributed
Dependable Computing”
Kamilla Klonowska, Lars Lundberg, Hakan Lennerstad, Charlie Svahnberg
Proceedings of the 19th IEEE International Parallel and Distributed Processing
Symposium (IPDPS'05), Denver, Colorado, April 2005
VI “Optimal Recovery Schemes in Fault Tolerant Distributed Computing”
Kamilla Klonowska, Lars Lundberg, Hakan Lennerstad, Charlie Svahnberg
Acta Informatica, 41(6), 2005
Publications that are related but not included in this thesis:
VII “Using Optimal Голомбо Rulers for Minimizing Collisions in Closed Hashing”
Lars Lundberg, Hakan Lennerstad, Kamilla Klonowska, Goran Gustafsson
Proceedings of Advances in Computer Science - ASIAN 2004, Higher-Level
Decision Making, 9th Asian Computing Science Conference, Thailand, December
2004; Lecture Notes in Computer Science, 3321 Springer 2004, ISBN 3-
540-24087-X
VIII “Bounding the Minimal Completion Time in High Продуктивність Parallel
Processing”
Lars Lundberg, Magnus Broberg, Kamilla Klonowska
International Journal of High Продуктивність Computing and Networking, Vol. 2,
No. 1, 2004
IX “Comparing the Optimal Продуктивність of Multiprocessor Architectures”
Lars Lundberg, Kamilla Klonowska, Magnus Broberg, Hakan Lennerstad
Proceedings of the twenty-first IASTED International Multi-Conference Applied
Informatics AI 2003, Innsbruck, Austria, February 2003
X “Recovery Schemes for High Availability and High Продуктивність Distributed
Real-Time Computing”
Lars Lundberg, Daniel Haggander, Kamilla Klonowska, Charlie Svahnberg
Proceedings of the 17th International Parallel & Distributed Processing Symposium
IPDPS 2003, Nice, France, April 2003
XI “Evaluating Heuristic Scheduling Algorithms for High Продуктивність Parallel
Processing”
Lars Lundberg, Magnus Broberg, Kamilla Klonowska
Proceedings of the fifth International Symposium on High Продуктивність Computing
ISHPC-V 2003, Tokyo, Japan, October 2003
XII “A Method for Bounding the Minimal Completion Time in Multiprocessors”
Magnus Broberg, Lars Lundberg, Kamilla Klonowska
Technical Report, Blekinge Institute of Technology, 2002
XIII “Optimal Продуктивність Comparisons of Massively Parallel Multiprocessors”
Hakan Lennerstad, Lars Lundberg, Kamilla Klonowska
Підписано для публікації.
Зміст
Теоретичні Аспекти на Границі Продуктивності і Толерантність Дефекту в Паралельних обчисленнях.
1. Вступ ...................................................................................... ............................... ...................................... 3
1.1 Дослідницькі Питання ..................................................................... ............................... .................................... 5
1.2 Дослідницька Методологія ...................................................................... ............................... ........................... 6
1.3 Дослідницький Вклад .............................................................................. ............................... ............................ 6
2. Планування Мільтипроцессора (Частина I)................... ........................................................................ 8
2.1 Класифікація планування задач ..................................................... ..... ............................................................... 8
2.2 Межі і Складність на Плануванні Мультипроцессора ............................... ............................... .....................10
3. Завантаження Балансування і Толерантність Дефекту (ДРУГА Частина) ..................................... 12
3.1 Модель Дефекту ..................................................................................... .............................. ............................. 12
3.2 Надійність проти Придатності .................................................. .............................. ......................................... 13
4. Підведення підсумків Статті ............................................... .............................. ..................................... 15
4.1 Частина 1 ..................................................................................... .............................. ......................................... 15
4.2 Частина 2 .............................................................................. .............................. ................................................ 17
5. Майбутня Робота ....................................................... .............................. ................................................ 21
6. Посилання .................................................................................................................................................. 22
Додатки
Стаття1. Порівняння Оптимального Виконання Паралельної Архітектури ..................................29
Стаття2. Максимальна Вигода Збільшення Числа Вивантажень у мультипроцессорному плануванні............................................ .............................. .............................. ....................................... 67
Стаття 3. Користування Правилами Голомбо для Оптимальних Схем відновлення
толерантності помилок в рорзподіленгому обчисленні ............................................................... 87
Стаття4. Користування Правилами Модуло для Оптимальних Схем відновлення в
в рорзподіленгому обчисленні.......................................................... ................................................ 105
Стаття5. Розширенні правила Голомбо в нових схемах відновлення в
Розподіленому залежному обчисленні ................... .......................................................................... 125
Стаття 6. Оптимальні схеми відновлення при можливій толерантності помилки в
розподіленому обчисленні .......................................................... ..................................................... 143
Теоретичні Аспекти на Межі Продуктивності і Толерантність Дефекту в Паралельному Обчисленні
1 Вступ
Якщо однопроцессорна система не дає відповідної продуктивності, то єдиною альтернативою для підвищеня продуктивності є виконання тієї ж самої операції на декількох процесорах, які працюють паралельно.
Щоб збільшити виконання в паралельному обчисленні, ми захотіли б розподілити робочий між процесорами (комп'ютерами) як можна рівніше. Ця техніка має назву «Баланс Наавнтаження». Є багато шляхів здійсненння паралельних обчислень на паралельно працюючих процессорах. Один з них - вільно пов'язана паралельна система, що полягає у поєднанні автономних комп'ютерів, сполучених мережею, де процес може тільки виконуватись процесором, на якому він був запущений. Це розподілення процесів між процесорами називається статичним розподілом.
Вільно пов'язана паралельна система дуже приваблива із-за її низької вартості в придатності і відмовостійкості. Якщо один комп’ютер, що виконував обчислення, віипадково відмовляє, то його роботу може перейняти інший робочий комп’ютер що включений в систему.
Але є одна багатообіцяюча проблема у вільно пов'язаних системах – це спланувати процеси серед процесорів щоб досягти деяких результатів продуктивності, а також зменшити затримки комунікації
і час завершення. Час завершення виконання має назву «робочий інтервал.»
Інша паралельна система - жорстко пов'язана Симетрична Багатопроцесорна система (SMP), яка складається з множинних подібних процесорів в межах того ж комп'ютера, зв'язаних шиною або деякою іншою швидкою мережею взаємного зв'язку. Тут процес може виконуватися різними процесорами впродовж періодів різного часу.
Це розміщення процесів до процесорів називається динамічним розподілом. Система SMP пропонує високу продуктивність і ефективне балансування завантаження, але не є особливо придатною. Якщо один процесор дає збій, то і весь обрахунок потерпить невдачу.
Одна із проблем, що часто викликає зацікавлення, виникає в поліпшенні виконання, скорочуючи при цьому час завершення паралельної програми, що складається з ряду синхронізуючої статики процесів. Також сюди відноситься і конфлікт між виконанням завдань і комунікації між ними.
Один критичний приклад - паралельна програма, яка виконується на одному процесорі. На цю програму не впливає синхронізація комунікації, але вона страждає від серйозної нестійкості завантаження. З іншого боку, якщо та ж програма паралельно виконується на багатьох процесорах, то завантаження, може бути рівномірно поширеним на процесори, але вартість комунікації може бути дуже висока.
Знахідка алгоритму планування, який мінімізує час завершення для паралельно виконуваних програм, складається з ряду процесів - один з класичної інформатики проблеми, що є показано в класі складності NP.
Декілька хороших евристичних методів були запропоновані, але важко знати, коли необхідно зупинити евристику і знайти кращі графіки. Тому важливо знати оптимальні межі, щоб з'ясувати, як близько/далеко алгоритми від оптимальних результатів. Важливе питання - те, скільки виконань можливо здійснити, дозволяючи динамічне розміщення, за умови, що ми можемо знайти (майже) оптимальне планування і виконання алгоритмів. Відповідь на це питання забезпечила б важливе введення, коли ми хочемо щоб балансувати додаткову вартість і складність дозволу динамічному розподілу навантаження втрата обмеження самого себе до статичного розподілу. У статті 2 ми визначаємо функцію, що відповідає на це питання для дуже широкого діапазону мультипроцесорів і паралельних програмах.
Інша можливість збільшити продуктивність - дозволити пріоритетне переривання. У пріоритетному прериванні процес може бути перерваний іншими процесами, а потім відновлений на іншому процесорі. Планування з пріоритетними перериваннями гнучкіше, але це не завжди можливо, і пріоритетні переривання можуть бути дорогі із-за накладних витрат. Пріоритетне переривання може бути зроблене у будь-який момент.
Тут стан має бути збережено перед тим, як процес буде вивантажений а потім відновлений, коли виконання відновлюється. Це означає, що з одного боку пріоритетні переривання потрібні для того, щоб отримати балансне завантаження, однак, з іншого боку буває потрібно обмежити число пріоритетних переривань для того, щоб мінімізувати накладні витрати. Оптимальне рішення до цієї проблеми залежить від ряду параметрів, як наприклад вартість для вивантаження, а пізніше - повторний запуск процесу. Вигода в продуктивності можлива, якщо число пріоритетних переривань підвищують, припускаючи, що немає ніяких накладних витрат.
У Статті 2 ми представляємо щільну верхню межу при максимальній вигоді збільшення числа пріоритетних переривань для будь-якої паралельної програми.
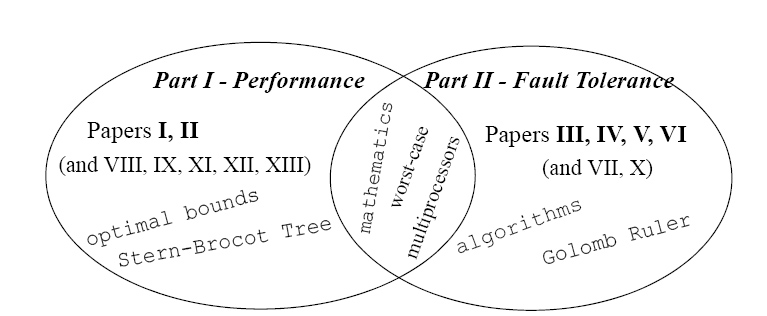
У паралельних системах, що мають можливість обробки толерантності помилок, є можливість отримання техніки відмовостійкості. У найпростішому випадку, маючи два комп'ютери, один є активним, а один - для резервування. Якщо первинні комп'ютерні збої проявляються, то помічник просто приймає роботу. Для того, щоб отримати вищу придатність, треба використовувати більш ніж тільки два комп'ютери. Проте, це може бути найдорожча для формування велика кластерна система з багатьма резервними комп'ютерами. Це часто привабливіше, ніж терпіти невдачу з комп'ютерами, які вже активні в системі, але це важко для вирішення на якому з терплячих невдачу комп'ютерів треба виконувати. Це є особливо важко, якщо це рішення доведеться зробити статично до програмних запусків виконання. Мета тут - знайти схему повторного поширення, яка підтримує високу продуктивність навіть тоді, коли один або більше комп'ютерів ламаються. У статтях 3-4 ми відобразили чотири схеми різного повторного поширення. Доклад представлений у вигляді 2х частин: перша у вигляді статтяі, що відповідає першій частині і частині другій роботи, а також їх перетині перетин стандартних концепцій.
У обох частинах ми користуємося теоретичною технікою, яка призводить до завідомо погано працюючих програм і сценаріїв. Коректність заснована на математичних доказах.
Зокрема ми відображаємо межі продуктивності на коефіцієнті впродовж мінімального часу завершення паралельної програми, що виконується за 2м сценарієм. Сценарій один: коефіцієнт для мінімального часу завершення, коли процеси можуть бути перерозподілені, порівнюємо з тим, коли вони не можуть бути перерозподілені на інші процесори впродовж їх тривалості виконання.
Сценарій два: коли графік пріоритетний, ми використовуємо різне число пріоритетних переривань.
У другій частині ми обговорюємо проблему повторного поширення завантаження серед працюючих комп'ютерів в паралельній системі, якщо один абл більше більше комп'ютерів в системі ламаються. Тут ми представляємо чотири алгоритми (Статтяи III, IV, V і VI) різного повторного поширення.
У Секції 3 класифікація дефектів має відношення до роботи в системі толерантності дефекту представленя.