Вопрос 3. Средние показатели в рядах динамики.

Для получения обобщающих показателей динамики определяются средние величины.

Средний уровень ряда динамики характеризует типическую величину абсолютных уровней и определяется делением суммы уровней y_i на их число n:

= . (13)

Для моментного ряда динамики с равноотстоящими моментами времени средний уровень исчисляется по формуле:

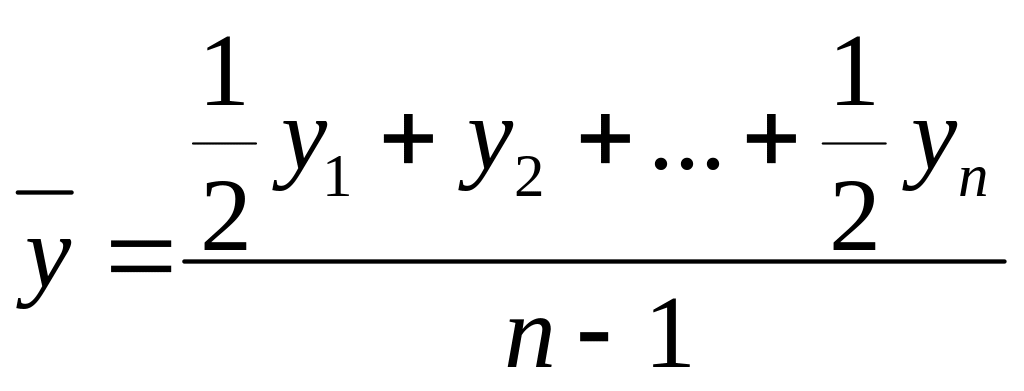(14)

Для моментного ряда динамики с неравноотстоящими моментами времени средний уровень находится по формуле:

, (15)

здесь у_i - уровни ряда, не изменяющиеся в течение промежутка времени t_i.

Средний абсолютный прирост определяется как сумма абсолютных приростов, деленная на их число:

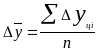. (16)

Средний абсолютный прирост можно определить по абсолютным уровням как разность конечного уровня ряда и начального (базисного) уровня, деленную на число субпериодов

(17)

Средний темп роста - это обобщающая характеристика индивидуальных темпов роста ряда динамики, определяемая как корень степени n из произведения индивидуальных цепных темпов роста, выраженных в коэффициентах:

, (18)

где Т_рi - индивидуальные (цепные) темпы роста (в коэффициентах), n - их число.

Определим средний темп роста с использованием абсолютных уровней ряда:

(19)

Средний темп прироста определяется на основе взаимосвязи между темпами роста и прироста

при расчете в коэффициентах (20)

Применение понятий:

По данным предыдущей таблицы определим средние показатели РД:

1. Средний уровень РД:

= = 983,1 тыс. у.е.

2. Средний абсолютный прирост (по цепным)

=

или = тыс. у.е.

или = тыс. у.е.

3. Средний темп роста:

или 105,3 %

или

или 105,3%

4. Средний темп прироста

=1,053 - 1 = 0,053 или 5,3 %/

Выводы: За анализируемый период среднегодовое значение товарооборота составляло 983,1 тыс.у.е. Товарооборот повышался ежегодно в среднем на 5,3% или на 50,7 тыс.у.е. Значение уровня товарооборота текущего года составляло в среднем 105,3% к уровню товарооборота предыдущего года.

Вопрос 4. Сглаживание рядов динамики. Скользящие средние. Экспоненциальное сглаживание.

Изменение уровней ряда динамики происходит под действием ряда факторов, неоднородных по силе, направлению и времени их действия. Постоянно действующие факторы формируют тренд или основную тенденцию развития. Наиболее распространенными методами статистического изучения тренда являются следующие:

1) Метод укрупнения интервалов. Это один из наиболее простых приемов обнаружения общей тенденции развития явления. Суть этого метода заключается в преобразовании первоначального ряда в ряд динамики с более продолжительным периодом или интервалом времени. Так ряд данных, содержащий данные о выпуске продукции за месяц можно преобразовать в ряд квартальных данных. При суммировании уровней отклонения, обусловленные случайными причинами, взаимопогашаются, сглаживаются и более четко обнаруживается действие основных факторов изменения уровней (общая тенденция).

Практическое использование:

Имеются данные о реализации радиоприемников в магазинах города (шт.)

Месяц	Число радиоприемников	Месяц	Число радиоприемников
Январь	3662	Июль	3803
Февраль	3096	Август	3812
Март	2956	Сентябрь	3921
Апрель	3805	Октябрь	4442
Май	3364	Ноябрь	3824
Июнь	2946	Декабрь	3976

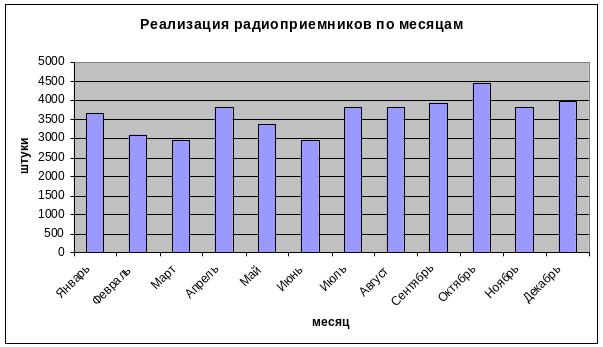
По отдельным месяцам уровни ряда имеют различные направления изменений. Поэтому затруднен вывод об основной тенденции продажи радиоприемников.

Выполним суммирование уровней ряда по месяцам и образуем ряд динамики по кварталам.

Кварталы	Число радиоприемников
1 квартал	9714
2 квартал	10115
3 квартал	11536
4 квартал	12242

2) Сглаживание методом скользящей средней.

По исходным данным определяются теоретические уровни, в которых случайные колебания погашаются, а основная тенденция развития выравнивается в виде плавной линии.

Для определения скользящей средней формируются укрупненные интервалы, состоящие из одинакового числа уровней. Каждый последующий интервал получается присоединением одного уровня справа и удалением одного уровня слева. Так мы постепенно сдвигаемся от начального уровня динамического ряда на один уровень. Тогда первый интервал включает уровни от у₁ до у_m ; второй интервал включает уровни от у₂ до у_m+1 и т.д.

Таким образом, интервал сглаживания как бы скользит по динамическому ряду с шагом, равным единице. По сформированным укрупненным интервалам определяем сумму значений уровней, на основе которых рассчитывается среднее (скользящее среднее). Полученное среднее относится к середине укрупненного интервала. Поэтому технически удобнее укрупненный интервал составлять из нечетного числа уровней ряда. При четном числе уровней ряда в укрупненных интервалах необходима дополнительная процедура центрирования.

Величина интервала сглаживания зависит от средней длины цикла в изучаемом ряду динамики. Это необходимо чтобы исключить циклические колебания. Обычно величина интервала сглаживания равна целому числу, кратному средней длине цикла.

Практическое использование:

Данные о доходах компании Cabot Corporation. Указанная компания имеет штаб-квартиру в Бостоне. Компания специализируется на производстве и продаже химикатов, строительных материалов, продуктов тонкой химии, полупроводников и сжиженного природного газа. Она имеет 39 заводов в 23 странах. Рыночная стоимость компании составляет около 1,87 млрд.долл.

Таблица. Доходы компании Cabot Corporation* в 1982-2001 годах (млрд. долл)

Год	Доход	Год	Доход	Год	Доход
1982	1587,7	1989	1936,9	1996	1870
1983	1558,0	1990	1684,7	1997	1640
1984	1752,5	1991	1488,0	1998	1650
1985	1407,5	1992	1562,2	1999	1700
1986	1309,9	1993	1618,5	2000	1690
1987	1424,0	1994	1686,6	2001	1520
1988	1676,6	1995	1840,9

Доходы компании за указанный период приведены на рис.

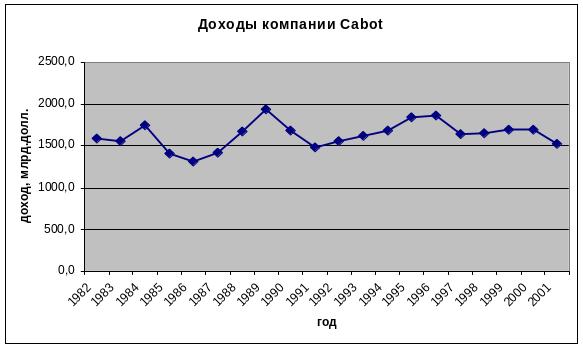
Как видно, долговременная тенденция изменения доходов затемнена большим количеством колебаний.

Предположим, что надо вычислить трехлетние скользящие средние значения. Первое скользящее среднее вычисляется путем суммирования данных о доходах за первых три годах с последующим делением на три.

Второе трехлетнее скользящее среднее вычисляется путем суммирования данных о доходах по годам со 2-го по 4-й и делением суммы на три.

Этот процесс будет продолжаться, пока не будет вычислено скользящее среднее для последних трех лет.

Год	Доход	3-летние MA	7-летние MA
1982	1587,7	#Н/Д	#Н/Д
1983	1558,0	1632,7	#Н/Д
1984	1752,5	1572,7	#Н/Д
1985	1407,5	1490,0	1530,9
1986	1309,9	1380,5	1580,8
1987	1424,0	1470,2	1598,9
1988	1676,6	1679,2	1561,1
1989	1936,9	1766,1	1583,2
1990	1684,7	1703,2	1627,3
1991	1488,0	1578,3	1664,8
1992	1562,2	1556,2	1688,3
1993	1618,5	1622,4	1678,0
1994	1686,6	1715,3	1671,2
1995	1840,9	1797,6	1694,7
1996	1870		1714,2
1997	1640	1720	1725,6
1998	1650	1663	1702,2
1999	1700	1680	#Н/Д
2000	1690	1637	#Н/Д
2001	1520		#Н/Д

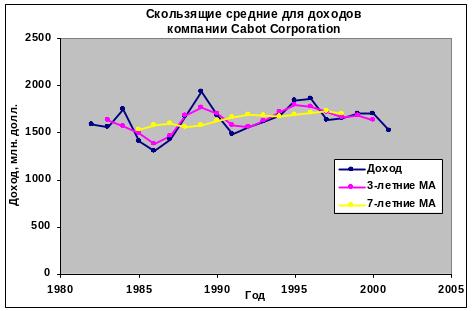
Как видно из рис. семилетние скользящие средние намного больше сглаживают ряд динамики, чем трехлетние. Это происходит потому, что семилетним скользящим средним соответствует более долгий период. Однако, чем больше длина периода, тем меньшее количество скользящих средних можно вычислить и отобразить на графике. Выпадающие из анализа значения приводят к искажению ряда динамики.

Чтобы избежать утомительных вычислений на практике применяется программное обеспечение (Пакет анализа программы Microsoft Excel).

3) Экспоненциальное сглаживание.

Для выявления долговременных тенденций применяется метод экспоненциального сглаживания. Этот метод позволяет делать краткосрочные прогнозы (в рамках одного интервала), когда наличие долговременных тенденций остается под вопросом.

Метод получил название от последовательности экспоненциально взвешенных скользящих средних. Каждое значение этой последовательности зависит от всех предыдущих наблюдаемых значений.

Уравнение, позволяющее сгладить ряд динамики в пределах произвольного периода времени i содержит три элемента:

Текущее наблюдаемое значение У_i , принадлежащее ряду динамики;

Предыдущее экспоненциально сглаженное значение Е_i-1

Присвоенный вес W.

(21)

Здесь Е_i - экспоненциально сглаженное i-е значение;

Е_i-1 - экспоненциально сглаженное i-1-е значение;

У_i - наблюдаемое исходное i - е значение ряда динамики;

W - сглаживающий коэффициент (0<W<1).

Выбор сглаживающего коэффициента достаточно субъективен. Если исследователь хочет просто исключить из ряда динамики нежелательные циклические или случайные колебания, следует выбирать небольшие величины W (близкие к нулю). В этом случае четко проявляются долговременные тенденции.

Если ряд динамики используется для прогнозирования, необходимо выбрать большой вес W (близкий к 1). Тогда повышается точность краткосрочного прогнозирования.

Практическое использование:

На рис. Показаны графики экспоненциально сглаженного ряда динамики (W=0,50 и W=0,25) для данных о доходах компании Cabot Corporation.

Год	Доход	ЭС (W=0.50)	ЭС (W=0.25)
1982	1587,7	1587,7	1587,7
1983	1558,0	1572,9	1580,3
1984	1752,5	1662,7	1623,3
1985	1407,5	1535,1	1569,4
1986	1309,9	1422,5	1504,5
1987	1424,0	1423,2	1484,4
1988	1676,6	1549,9	1532,4
1989	1936,9	1743,4	1633,6
1990	1684,7	1714,1	1646,3
1991	1488,0	1601,0	1606,8
1992	1562,2	1581,6	1595,6
1993	1618,5	1600,1	1601,3
1994	1686,6	1643,3	1622,7
1995	1840,9	1742,1	1677,2
1996	1865,2	1803,7	1724,2
1997	1636,7	1720,2	1702,3
1998	1652,8	1686,5	1689,9
1999	1699,0	1692,7	1692,2
2000	1698,0	1695,4	1693,7
2001	1523,0	1609,2	1651,0

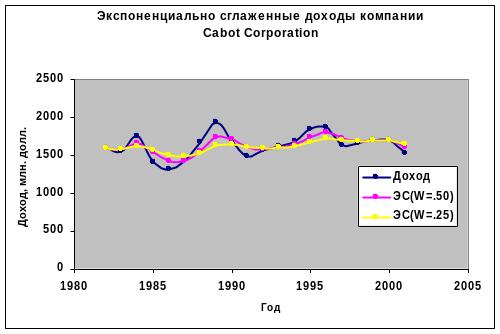
Допустим, что коэффициент сглаживания равен 0,25. Первое наблюдаемое значение, равное У₁₉₈₂ =1587,7, одновременно является первым сглаженным значением

Е₁₉₈₂ =1587,7. Используя значение ряда динамики для 1983 года (У₁₉₈₃ =1558,0), получаем следующее сглаженное значение для 1983 года:

Сглаженное значение для 1984 года:

Сглаженное значение для 1985 года:

Этот процесс продолжается пока не будут сглажены все 19 значение ряда динамики.

Экспоненциально сглаженное i - значение можно использовать в качестве оценки предсказанного (i+1) – го значения.

Прогнозирование величины для (i+1) – го значения

- прогнозное значение.

Для предсказания доходов компании Cabot Corporation в 2002г. на основе экспоненциально сглаженного временного ряда, соответствующего весу W=0,25, можно использовать сглаженное значение, вычисленное для 2001г. Из табл. видно, что эта величина равна 1651,0 млн. долл.

млн. долл.

Предскажем уровень доходов в 2003 году, используя сглаженное значение доходов в 2002 году:

(21А)

Иначе говоря, формулы для прогнозирования выглядят следующим образом:

Текущее сглаженное значение = W*(текущее наблюдаемое значение)+(1-W)*

*( предыдущее сглаженное значение).

Новый прогноз = W*( текущее наблюдаемое значение) + (1-W)*(текущий прогноз).