Вопрос 13.

Стационарное движение жидкости в прямолинейной трубе. Фор­мула Пуазейля. Пусть вязкая несжимаемая жид­кость течет вдоль прямо­линейной цилиндрической трубы радиусом R. Линии тока парал­лельны оси трубы.

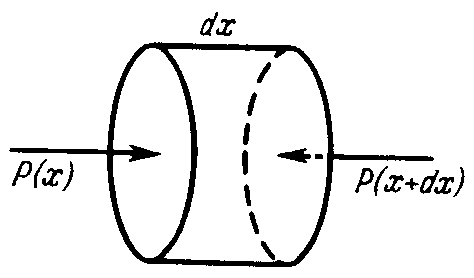
Если выделить беско­нечно узкую трубку (рис. 13), то из ус­ло­вия не­сжимаемости последует, что ско­рость течения вдоль всей трубки тока будет одна и та же. Конечно, скорость изме­ня­ется по радиусу трубы .

Примем за ось трубы ось X, направ­лен­ную в сторону течения жидко­сти. Вы­делим в трубе произвольный цилиндрический эле­мент длиной dx и ра­диуса r. На его боковую поверхность в направлении движения действует касательная сила вязко­сти: .

В том же направлении на основания этого цилиндра действует сила разности давлений: .

При течении стационарном сумма этих двух сил должна быть равна нулю, поэтому: .

Ясно, что по оси X подбирается постоянным и таким, чтобы и, сле­довательно, и не меняются с изменением X. Тогда , где р₁, р₂ - давление на входе и вы­ходе трубы, соответственно.

Приходим к следующей форме уравнения: .

Интегрируя его, получаем: .

Постоянная С определяется из краевых условий: на стенке трубы при r = R, скорость должна обращаться в ноль. Это дает

.

Получаем промежуточный результат: - на оси трубы (r = 0), а при уда­лении от оси спадает по параболическому закону.

Определим расход жидкости: количество жидкости, ежесекундно про­те­кающее через поперечное сечение трубы. В общем случае - масса жидкости, ежесекундно протекающая через кольцо с внутренним ра­диусом r и внешним r + dr. Подставим выраже­ние скоро­сти и проинтегри­руем по r:

или . Формула Пуазейля (1799 - 1869)

Расход жидкости пропорционален разности давлений, четвертой сте­пени радиуса трубы и обратно пропорционален длине трубы и вязко­сти текущей жидкости. Формула была экспериментально получена неза­висимо в 1839 г. Гагеном (исследовал движение воды в трубах) и в 1840 г. Жаном Пуазейлем (течение жидкостей в капиллярах). Формула Пуа­зейля справед­лива только для ламинарных течений жидкости. Ламинар­ное (слоистое) течение - час­тицы жидкости движутся вдоль прямоли­нейных траекторий, параллельных оси трубы. При больших скоростях ламинарное течение ста­новится неустой­чивым и переходит в турбулент­ное течение, к которому формула Пуазейля неприменима.

Метод размерностей позволяет получить законы Пуазейля в более об­щем виде для случая прямолинейных труб произвольного попереч­ного се­чения: , где С - постоянная характеризующая форму попе­речного сечения и определяемая чаще всего эксперимен­тально.

Вопрос 14.

Элементы теории гидродинамического подобия. Пусть имеется произ­вольный изотермический поток жидкости, обтекающий какое-ни­будь тело или систему тел. Интуи­тивно понятно, что можно данное рас­положе­ние тел и течений с той или иной точностью повторить, т.е. соз­дать подо­бие системы. При этом, од­нако, надо повторить основные па­раметры дан­ной сис­темы: ; ; ; l; ; c; g; , где и - радиус-век­тор и скорость жидкости в подобно расположенных точках, l - характер­ный размер, - характерная скорость потока (например, скорость жид­кости, с которой она из «бесконеч­ности» натекает на рассматриваемую систему тел), - плот­ность жидкости, - вязкость, с - скорость звука в рассматриваемой жидко­сти (ее используют вместо сжимаемости), g - ус­корение свободного паде­ния (вво­дят, если суще­ственно гравитационное поле), - характерное время заметного измене­ния течения (используют при нестационарном те­чении).

Пытаясь создать идентичные системы, экспериментаторы пришли к вы­воду, что идентичность по совокупности и по каждому параметру созда­вать не надо. Необходимо, чтобы системы были аналогичны или подобны. А так как параметры системы, вообще говоря, могут быть раз­личны, то удобно пользоваться функциональными, безразмерными ко­эффициентами (несу­щими большую качественную информацию о сис­теме).

Представим шесть основных безразмерных комбинаций этих па­ра­мет­ров: 1. ; 2. ; 3. Число Рейнольдса: ; 4. Число Фруда: ; 5. Число Маха: ; 6. Число Струхаля: .

Безразмерные отношения и числа, являясь безразмерными коэф­фи­циен­тами в уравнении движения вязкой жидкости, выступают в каче­стве крите­риев гидродинамического подобия (табл. 1).

Таблица 1. Основные критерии подобия

Символ и фор­мула критерия	Наименование	Физический смысл
	Критерий подобия поля ско­ростей	Характеризует поле ско­ро­стей, яв­ляясь отноше­нием скорости тече­ния в каждой данной точке к харак­терной для этого течения скорости
	Критерий геометриче­ского подобия	Характеризует масштаб­ное распо­ложение эле­ментов жидкости отно­сительно и по отношению к харак­тер­ному размеру
	Критерий режима движе­ния. Число Рейнольдса	Характеризует режим дви­жения при вынужден­ной конвекции, явля­ясь отно­шением сил инерции и сил вязкости
	Критерий гравитацион­ного подобия. Число Фруда	Характеризует соотноше­ние сил тяжести и сил инерции в потоке
	Критерий сжимаемости жидкости. Число Маха	Характеризует сжимае­мость жид­кости при уве­личении ее характер­ной скорости
	Критерий гидродинамиче­ской гомохронности. Число Струхаля	Характеризует меру от­но­шения пе­реносного (кон­вективного) ускоре­ния к ускорению в данной точке

В виду особой важности двух критериев Re и F дадим иное их тол­ко­ва­ние, дополнительно к табличному. По порядку величины число Рей­нольдса есть отношение кинетической энергии жидкости к потере ее, обу­словленной работой сил вязкости на ха­рактерной длине. По порядку вели­чины число Фруда определяет отноше­ние кинетической энергии жидкости к приращению ее, обусловленному работой силы тяжести на пути, равному характерной длине. Чем больше F - тем больше роль инерции по сравне­нию с тяжестью.

По правилу размерности каждая комбинация является функцией ос­таль­ных, например: = f( ; Re; F; M; S). Если для 2-х течений совпа­дают 5, то совпадают и 6-е. Это - общий закон подобия течений, а течения называют механически или гидродинамически подоб­ными.

Пример пользования: а) для стационарных течений , а следова­тельно и S обращаются в ; б) для несжимаемых жидкостей М = 0. Та­ким образом, для условий а) + б):  , т.е. течения по­добны, если они имеют одинаковые Re и F.