
- •175. Навіщо потрібні криптографічні протоколи.
- •176. Гібридні криптосистеми.
- •177. Цифровий підпис.
- •181. Екранування, аналіз захищеності.
- •182. Антивірус Касперського.
- •Антивірус Касперського 2010 Базовий захист
- •183. Антивірус BitDefender.
- •184. Антивірус Dr.Web.
- •Характерные особенности
- •185. Антивірус nod32.
- •186. Поняття та переваги мови асемблера. Запис лексем. Запис рядків.
- •Ссылки вперед
- •Большой размерности
- •31 (Таким образом, этот флаг можно использовать для операций над числами
- •Команда сравнения
- •Безусловные переходы
- •Команда безусловного перехода
- •Команды условного перехода и флаги
- •228 Глава 10. Команды передачи управления
- •Xor: Если один из сравниваемых битов равен 0, а другой равен 1, то результат равен 1; если сравниваемые биты одинаковы (оба - 0 или оба - 1) то результат - 0.
Xor: Если один из сравниваемых битов равен 0, а другой равен 1, то результат равен 1; если сравниваемые биты одинаковы (оба - 0 или оба - 1) то результат - 0.
TEST: действует как AND-устанавливает флаги, но не изменяет биты.
Первый операнд в логических командах указывает на один байт или слово в регистре или в памяти и является единственным значением, которое может изменятся после выполнения команд. В следующих командах AND, OR и XOR используются одинаковые битовые значения:
AND OR XOR 0101 0101 0101 0011 0011 0011 ---- ---- ---- Результат: 0001 0111 0110
Для следующих несвязанных примеров, предположим, что AL содержит 1100 0101, а BH содержит 0101 1100:
1. AND AL,BH ;Устанавливает в AL 0100 0100 2. OR BH,AL ;Устанавливает в BH 1101 1101 3. XOR AL,AL ;Устанавливает в AL 0000 0000 4. AND AL,00 ;Устанавливает в AL 0000 0000 5. AND AL,0FH ;Устанавливает в AL 0000 0101 6. OR CL,CL ;Устанавливает флаги SF и ZF
Примеры 3 и 4 демонстрируют способ очистки регистра. В примере 5 обнуляются левые четыре бита регистра AL. Хотя команды сравнения CMP могут быть понятнее, можно применить команду OR для следующих целей:
1. OR CX,CX ;Проверка CX на нуль JZ ... ;Переход, если нуль 2. OR CX,CX ;Проверка знака в CX JS ... ;Переход, если отрицательно
Команда TEST действует аналогично команде AND, но устанавливает только флаги, а операнд не изменяется. Ниже приведено несколько примеров:
1. TEST BL,11110000B ;Любой из левых бит в BL JNZ ... ; равен единице? 2. TEST AL,00000001B ;Регистр AL содержит JNZ ... ; нечетное значение? 3. TEST DX,OFFH ;Регистр DX содержит JZ ... ; нулевое значение?
Еще одна логическая команда NOT устанавливает обpатное значение бит в байте или в слове, в регистре или в памяти: нули становятся единицами, а единицы - нулями. Если, например, pегистр AL содержит 1100 0101, то команда NOT AL изменяет это значение на 0011 1010. Флаги не меняются. Команда NOT не эквивалентна команде NEG, которая меняет значение с положительного на отрицательное и наоборот, посредством замены бит на противоположное значение и прибавления единицы.
198) Творчески сочетая сдвиги и умножения, можно организовать быстрое умножение на почти любое конкретное значение. Следующий фрагмент производит умножение значения в регистре AX на 10:
mov bx, ax ; скопировать исходное число
shl ax, 1 ; * 2
shl ax, 1 ; * 4
add ax, bx
shl ax, 1 ; * 10
Использование отказа от универсальности для деления несколько болле ограничено. Деление на степень двойки, конечно, очень просто. Вы просто сдвигаете число вправо, следя лишь за выбором родходящей команды сдвига для желаемого типа деления (со знаком или без знака). Например, для выполнения деления без знака на 4 содержимого регистра AX можно написать:
shr ax, 1
shr ax, 1
а для процессора 80186 и более поздних можно вместо этого использовать команду
shr ax, 2
Деление со знаком на 4 обеспечит, например, последовательность
sar ax, 1
sar ax, 1
или для процессора 80186 и более поздних
sar ax, 2
199.
В языке ассемблера имеются средства записи целых и вещественных чисел, а также символьных строк и отдельных символов. Целые числа могут быть со знаком и без знака, а также записанными в двоично-десятичном формате. Для целых чисел и символов в составе команд микропроцессора и, соответственно, в языке ассемблера, есть средства обработки - анализа, сравнения, поиска и проч. Для вещественных чисел таких средств в самом микропроцессоре нет, они содержатся в арифметическом сопроцессоре. Рассмотрим сначала целые числа без знака и со знаком. Числа без знака получили свое название потому, что среди этих чисел нет отрицательных. Это самый простой вид чисел: они представляют собой весь диапазон двоичных чисел, которые можно записать в байте, слове или двойном слове. Для байта числа без знака могут принимать значения от 00h (0) до FFh (255); для слова - от 0000h (0) до FFFFh (65535); для двойного слова - от 00000000h (0) до FFFFFFFFh (4294967295). В огромном количестве приложений вычислительной техники для чисел нет понятия знака. Это справедливо, например, для адресов ячеек памяти, кодов ASCII символов, результатов измерений многих физических величин, кодов управления устройствами, подключаемыми к компьютеру. Для таких чисел естественно использовать весь диапазон чисел, записываемых в ячейку того или иного размера. Если, однако, мы хотим работать как с положительными, так и с отрицательными числами, нам придется половину чисел из их полного диапазона считатьположительными, а другую половину - отрицательными. В результате диапазон изменения числа уменьшается в два раза. Кроме того, необходимо предусмотреть систему кодирования, чтобы положительные и отрицательные числа не перекрывались. В вычислительной технике принято записывать отрицательные числа в так называемом дополнительном коде, который образуется из прямого путем замены всех двоичных нулей единицами и наоборот (обратный код) и прибавления к полученному числу единицы. Это справедливо как для байтовых (8-битовых) чисел, так и для чисел размером в слово или в двойное слово (рис. 1)
Рис. 1. Образование отрицательных чисел различного размера.
 Такой
способ образования отрицательных чисел
удобен тем, что позволяет выполнять над
ними арифметические операции по общим
правилам с получением правильного
результата. Так, сложение чисел +5 и -5
дает 0; в результате вычитания 3 из 5
получается 2; вычитание -3 из -5 дает -2 и
т.д.
Анализируя алгоритм образования
отрицательного числа, можно заметить,
что для всех отрицательных чисел
характерно наличие двоичной единицы в
старшем бите. Положительные числа,
наоборот, имеют в старшем бите 0. Это
справедливо для чисел любого размера.
Кроме того, из рис. 1 видно, что для
преобразования отрицательного 8-битового
числа в слово достаточно дополнить его
слева восемью двоичными единицами.
Легко сообразить, что для преобразования
положительного 8-битового числа в слово
его надо дополнить восемью двоичными
нулями. То же справедливо и для
преобразования слова со знаком в двойное
слово со знаком, только добавить придется
уже не 8, а 16 единиц или нулей. В системе
команд МП 86 и, соответственно, в языке
ассемблера, для этих операций предусмотрены
специальные команды cbw и cwd.
Следует
подчеркнуть, что знак числа условен.
Одно и то же число, например, изображенное
на рис. 1 8-битовое число FBh можно в одном
контексте рассматривать, как отрицательное
(-5), а в другом - как положительное, или,
правильнее, число без знака (FBh=251). Знак
числа является характеристикой не
самого числа, а нашего представления о
его смысле.
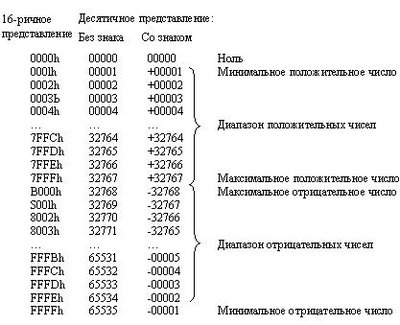
На рис. 2 представлена
выборочная таблица 16-битовых чисел с
указанием их машинного представления,
а также значений без знака и со знаком.
Из таблицы видно, что для чисел со знаком
размером в слово диапазон положительных
значений простирается от 0 до 32767, а
диапазон отрицательных значений - от
-1 до -32768.
Такой
способ образования отрицательных чисел
удобен тем, что позволяет выполнять над
ними арифметические операции по общим
правилам с получением правильного
результата. Так, сложение чисел +5 и -5
дает 0; в результате вычитания 3 из 5
получается 2; вычитание -3 из -5 дает -2 и
т.д.
Анализируя алгоритм образования
отрицательного числа, можно заметить,
что для всех отрицательных чисел
характерно наличие двоичной единицы в
старшем бите. Положительные числа,
наоборот, имеют в старшем бите 0. Это
справедливо для чисел любого размера.
Кроме того, из рис. 1 видно, что для
преобразования отрицательного 8-битового
числа в слово достаточно дополнить его
слева восемью двоичными единицами.
Легко сообразить, что для преобразования
положительного 8-битового числа в слово
его надо дополнить восемью двоичными
нулями. То же справедливо и для
преобразования слова со знаком в двойное
слово со знаком, только добавить придется
уже не 8, а 16 единиц или нулей. В системе
команд МП 86 и, соответственно, в языке
ассемблера, для этих операций предусмотрены
специальные команды cbw и cwd.
Следует
подчеркнуть, что знак числа условен.
Одно и то же число, например, изображенное
на рис. 1 8-битовое число FBh можно в одном
контексте рассматривать, как отрицательное
(-5), а в другом - как положительное, или,
правильнее, число без знака (FBh=251). Знак
числа является характеристикой не
самого числа, а нашего представления о
его смысле.
На рис. 2 представлена
выборочная таблица 16-битовых чисел с
указанием их машинного представления,
а также значений без знака и со знаком.
Из таблицы видно, что для чисел со знаком
размером в слово диапазон положительных
значений простирается от 0 до 32767, а
диапазон отрицательных значений - от
-1 до -32768.
Рис. 2 Представление 16-битовых чисел без знака и со знаком
 На
рис. 3 представлена аналогичная таблица
для 8-битовых чисел. Из таблицы видно,
что для чисел со знаком размером в байт
диапазон положительных значений
простирается от 0 до 127, а диапазон
отрицательных значений - от -1 до -128.
На
рис. 3 представлена аналогичная таблица
для 8-битовых чисел. Из таблицы видно,
что для чисел со знаком размером в байт
диапазон положительных значений
простирается от 0 до 127, а диапазон
отрицательных значений - от -1 до -128.
Рис. 3 Представление 8-битовых чисел без знака и со знаком
 Среди
команд процессора, выполняющих ту или
иную обработку чисел, можно выделить
команды, безразличные к знаку числа
(например, inc, add, test), команды, предназначенные
для обработки чисел без знака (mul, div, ja,
jb и др.), а также команды, специально
рассчитанные на обработку чисел со
знаком (imul, idiv, jg, jl и т.д.).
Рассмотрим
теперь другой вид представления чисел
- двоично-десятичный формат (binary-coded
decimal , BCD), используемый в ряде прикладных
областей. В таком формате выдают данные
некоторые измерительные приборы; он же
используется КМОП-часами реального
времени компьютеров IBM PC для хранения
информации о текущем времени. В МП 86
предусмотрен ряд команд для обработки
таких чисел.
Двоично-десятичный
формат существует в двух разновидностях:
упакованный и распакованный. В первом
случае в байте записывается двухразрядное
десятичное число от 00 до 99. Каждая цифра
числа занимает половину байта и хранится
в двоичной форме. Из рис. 4 можно заметить,
что для записи в байт десятичного числа
в двоично-десятичном формате достаточно
сопроводить записываемое десятичное
число символом h.
Среди
команд процессора, выполняющих ту или
иную обработку чисел, можно выделить
команды, безразличные к знаку числа
(например, inc, add, test), команды, предназначенные
для обработки чисел без знака (mul, div, ja,
jb и др.), а также команды, специально
рассчитанные на обработку чисел со
знаком (imul, idiv, jg, jl и т.д.).
Рассмотрим
теперь другой вид представления чисел
- двоично-десятичный формат (binary-coded
decimal , BCD), используемый в ряде прикладных
областей. В таком формате выдают данные
некоторые измерительные приборы; он же
используется КМОП-часами реального
времени компьютеров IBM PC для хранения
информации о текущем времени. В МП 86
предусмотрен ряд команд для обработки
таких чисел.
Двоично-десятичный
формат существует в двух разновидностях:
упакованный и распакованный. В первом
случае в байте записывается двухразрядное
десятичное число от 00 до 99. Каждая цифра
числа занимает половину байта и хранится
в двоичной форме. Из рис. 4 можно заметить,
что для записи в байт десятичного числа
в двоично-десятичном формате достаточно
сопроводить записываемое десятичное
число символом h.
Рис. 4 Упакованный двоично-десятичный формат
 В
машинном слове или в 16-разрядном регистре
можно хранить в двоично-десятичном
формате четырехразрядные десятичные
числа от 0000 до 9999 (рис.5).
В
машинном слове или в 16-разрядном регистре
можно хранить в двоично-десятичном
формате четырехразрядные десятичные
числа от 0000 до 9999 (рис.5).
Рис. 5 Запись десятичного числа 9604 в слове
 Распакованный
формат отличается от упакованного тем,
что в каждом байте записывается лишь
одна десятичная цифра (по-прежнему в
двоичной форме). В этом случае в слове
можно записать десятичные числа от 00
до 99 (см. рис. 6)
Распакованный
формат отличается от упакованного тем,
что в каждом байте записывается лишь
одна десятичная цифра (по-прежнему в
двоичной форме). В этом случае в слове
можно записать десятичные числа от 00
до 99 (см. рис. 6)
Рис. 6 Запись десятичного числа 98 в распакованном виде
 При
хранении десятичных чисел в аппаратуре
обычно используется более экономный
упакованный формат; умножение и
деление выполняются только с распакованными
числами, операции же сложения и вычитания
применимы и к тем, и к другим.
При
хранении десятичных чисел в аппаратуре
обычно используется более экономный
упакованный формат; умножение и
деление выполняются только с распакованными
числами, операции же сложения и вычитания
применимы и к тем, и к другим.
