
Метод topsis.
Даний метод передбачає, що найкращою є та альтернатива, що має так оцінки за всіма відібраними критеріями, які формують найменшу відстань до ідеального рішення, а найгіршою – навпаки, має такі оцінки, які характеризують найбільшу відстань до еталону.
На першому етапі побудова та нормалізація матриці здійснюється за допомогою rij:
Таблиця 7
Матриця рішень для методу TOPSIS
Альтернативи |
k1 |
k2 |
k5 |
k6 |
k8 |
k3 |
k4 |
k7 |
Вага |
0,15 |
0,13 |
0,08 |
0,1 |
0,06 |
0,12 |
0,19 |
0,17 |
А1 |
10 |
11 |
8 |
9 |
4 |
7 |
9 |
1,7 |
А2 |
8 |
5 |
6 |
9 |
5 |
7 |
8 |
1,8 |
А3 |
11 |
6 |
7 |
7 |
7 |
10 |
7 |
1,6 |
А4 |
15 |
7 |
6 |
6 |
9 |
6 |
6 |
1,6 |
А5 |
13 |
4 |
5 |
7 |
8 |
20 |
7 |
1,2 |
|
min |
min |
min |
min |
min |
max |
max |
Max |
А1 |
100 |
121 |
64 |
81 |
16 |
49 |
81 |
2,89 |
А2 |
64 |
25 |
36 |
81 |
25 |
49 |
64 |
3,24 |
А3 |
121 |
36 |
49 |
49 |
49 |
100 |
49 |
2,56 |
А4 |
225 |
49 |
36 |
36 |
81 |
36 |
36 |
2,56 |
А5 |
169 |
16 |
25 |
49 |
64 |
400 |
49 |
1,44 |
|
26,06 |
15,72 |
14,49 |
17,20 |
15,33 |
25,18 |
16,70 |
3,56 |
На наступному етапі отримуємо нормалізовану матрицю.
Таблиця 8
Нормалізована матриця
Альтернативи |
k1 * |
k2* |
k5* |
k6* |
k8* |
k3* |
k4* |
k7* |
Вага |
0,15 |
0,13 |
0,08 |
0,1 |
0,06 |
0,12 |
0,19 |
0,17 |
А1 |
0,38 |
0,70 |
0,55 |
0,52 |
0,26 |
0,28 |
0,54 |
0,48 |
А2 |
0,31 |
0,32 |
0,41 |
0,52 |
0,33 |
0,28 |
0,48 |
0,51 |
А3 |
0,42 |
0,38 |
0,48 |
0,41 |
0,46 |
0,40 |
0,42 |
0,45 |
А4 |
0,58 |
0,45 |
0,41 |
0,35 |
0,59 |
0,24 |
0,36 |
0,45 |
А5 |
0,50 |
0,25 |
0,35 |
0,41 |
0,52 |
0,79 |
0,42 |
0,34 |
Функція |
min |
min |
min |
min |
min |
max |
max |
max |
На другому етапі розбудовуємо зважену нормалізовану матрицю рішень, що передбачає зважування кожної альтернативи на її вагу.
Третій крок полягає у визначенні ідеально позитивних та ідеально негативних рішень, що передбачає вибір значень за кожним критерієм: для ідеально позитивних в мінімізуючи функціях – найменші, в максимізуючи – найбільші; для ідеально негативних – навпаки.
Таблиця 10
Зважена нормалізована матриця рішень
Альтернативи |
k1 * |
k2* |
k5* |
k6* |
k8* |
k3* |
k4* |
k7* |
Вага |
0,15 |
0,13 |
0,08 |
0,1 |
0,06 |
0,12 |
0,19 |
0,17 |
А1 |
0,057 |
0,091 |
0,044 |
0,052 |
0,0156 |
0,0336 |
0,1026 |
0,0816 |
А2 |
0,0465 |
0,0416 |
0,0328 |
0,052 |
0,0198 |
0,0336 |
0,0912 |
0,0867 |
А3 |
0,063 |
0,0494 |
0,0384 |
0,041 |
0,0276 |
0,048 |
0,0798 |
0,0765 |
А4 |
0,087 |
0,0585 |
0,0328 |
0,035 |
0,0354 |
0,0288 |
0,0684 |
0,0765 |
А5 |
0,075 |
0,0325 |
0,028 |
0,041 |
0,0312 |
0,0948 |
0,0798 |
0,0578 |
Обмеження |
≤ 14 |
≤11 |
≤9 |
≤9 |
≤5 |
≥7 |
≥7 |
≥1,7 |
Функція |
min |
min |
min |
min |
min |
max |
max |
max |
Ідеально позитивні та ідеально негативні альтернативи |
||||||||
↑↓ |
Min(↓) |
Min(↓) |
Min(↓) |
Min(↓) |
Min(↓) |
Max(↑) |
Max(↑) |
Max(↑) |
А+ |
0,0465 |
0,0325 |
0,028 |
0,035 |
0,0156 |
0,0948 |
0,1026 |
0,0867 |
А- |
0,087 |
0,091 |
0,044 |
0,052 |
0,0354 |
0,0288 |
0,0684 |
0,0578 |
На наступному етапі відбувається обчислення ступеня близькості для всіх альтернатив. Воно здійснюється за наступною методологією:
Для тих, що характеризує ідеальну позитивність рішень:
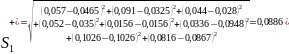
Для тих, що характеризує ідеальну негативність рішень:
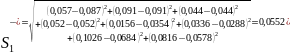
Відповідно до даних схем маємо наступні таблиці:
Таблиця 11
Розрахунок ідеально позитивної відстані
Альтернативи |
k1 * |
k2* |
k5* |
k6* |
k8* |
k3* |
k4* |
k7* |
S+ |
Вага |
0,150 |
0,130 |
0,080 |
0,100 |
0,060 |
0,120 |
0,190 |
0,170 |
|
А1 |
0,000 |
0,003 |
0,000 |
0,000 |
0,000 |
0,004 |
0,000 |
0,000 |
0,089 |
А2 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,004 |
0,000 |
0,000 |
0,065 |
А3 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,002 |
0,001 |
0,000 |
0,060 |
А4 |
0,002 |
0,001 |
0,000 |
0,000 |
0,000 |
0,004 |
0,001 |
0,000 |
0,091 |
А5 |
0,001 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,001 |
0,001 |
0,049 |
Таблиця 12
Розрахунок ідеально негативної відстані
Альтернативи |
k1 * |
k2* |
k5* |
k6* |
k8* |
k3* |
k4* |
k7* |
S- |
Вага |
0,150 |
0,130 |
0,080 |
0,100 |
0,060 |
0,120 |
0,190 |
0,170 |
|
А1 |
0,001 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,001 |
0,001 |
0,055 |
А2 |
0,002 |
0,002 |
0,000 |
0,000 |
0,000 |
0,000 |
0,001 |
0,001 |
0,076 |
А3 |
0,001 |
0,002 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,058 |
А4 |
0,000 |
0,001 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,043 |
А5 |
0,000 |
0,003 |
0,000 |
0,000 |
0,000 |
0,004 |
0,000 |
0,000 |
0,092 |
Наступний крок пов'язаний з обчисленням відносної близькості альтернативних рішень до ідеального за наступною методологією:
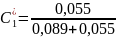
Таблиця 13
Відстані альтернатив до PIS та NIS
Альтернативи |
S+ |
S- |
|
Ранг |
|
А1 |
0,089 |
0,055 |
0,38 |
4 |
|
А2 |
0,065 |
0,076 |
0,54 |
2 |
|
А3 |
0,06 |
0,058 |
0,49 |
3 |
|
А4 |
0,091 |
0,043 |
0,32 |
5 |
|
А5 |
0,049 |
0,092 |
0,65 |
1 |
Графічно можемо зобразити отримане наступним чином:

Рис. 4. Ранжування альтернатив.
Висновки: за даним методом можемо зробити висновок, що найкращою альтернативою залишається 5-а – проведення маркетингового дослідження за допомогою формування он-лайн фокус-груп, оскільки даний метод є максимально наближеним до бажаного з врахуванням всіх критеріїв та їх значення, а найгіршим – є проведення опитування за методом eye-tracking, оскільки він менше всіх відповідає поставленим вимогам та обмеженням. Проте за даною оцінкою помінялися ранги 2-ої та 3-ої альтернатив, але вони не суттєво відрізняються.

