СЕВЕРО-ЗАПАДНЫЙ ГОСУДАРСТВЕННЫЙ ЗАОЧНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

МУРМАНСКИЙ ФИЛИАЛ

КОНТРОЛЬНАЯ РАБОТА

ПО ПРЕДМЕТУ:

«МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ

И СЕРТИФИКАЦИЯ»

ВЫПОЛНИЛА:

СТУДЕНТКА III КУРСА

СПЕЦИАЛЬНОСТИ 220100 ФИТСУ

АвксЁнова Ирина Николаевна

ШИФР: 34-0269

ПРОВЕРИЛ:

СЕРГУШЕВ Г.Ф.

« » 2006г.

МУРМАНСК

2006

ЗАДАНИЕ 1

При многократном измерении (n=60) напряжения с помощью цифрового вольтметра получен следующий массив данных, В:

	1	2	3	4	5	6	7	8	9	10
1	8,588	8,607	8,597	8,607	8,612	8,602	8,601	8,597	8,555	8,601
2	8,587	8,605	8,588	8,588	8,605	8,590	8,556	8,562	8,596	8,557
3	8,608	8,597	8,541	8,603	8,602	8,601	8,558	8,558	8,608	8,577
4	8,593	8,588	8,601	8,593	8,555	8,577	8,596	8,592	8,602	8,596
5	8,602	8,597	8,597	8,592	8,602	8,588	8,554	8,628	8,577	8,555
6	8,588	8,592	8,558	8,588	8,555	8,580	8,590	8,606	8,580	8,591

Поскольку разброс полученных экспериментальных данных свидетельствует о том, что результат измерений напряжения является случайной величиной, то более полное представление о результате измерений может дать гистограмма.

Для построения гистограммы выпишем значения массива данных в возрастающем порядке, указав для каждого значения число повторений в массиве данных.

i	1	2	3	4	5	6	7	8	9	10
U	8,541	8,554	8,555	8,556	8,557	8,558	8,562	8,577	8,580	8,587
mi	1	1	4	1	1	2	1	3	2	1

i	11	12	13	14	15	16	17	18	19	20
U	8,588	8,590	8,591	8,592	8,593	8,596	8,597	8,601	8,602	8,603
mi	8	2	1	3	2	3	5	4	5	1

i	21	22	23	24	25	26
U	8,605	8,606	8,607	8,608	8,612	8,628
mi	2	1	2	2	1	1

Перечисленные значения напряжения изменяются в пределах от 8,541В до 8,628В. Объединим перечисленные значения в шесть интервалов(l₁-l₆) с шагом ∆l=0,015 в диапазоне (l) от 8,54 до 8,63.

Интервал измеренных значений (li)	Число значений в интервале (mi)
1. 8,540 8,555	6
2. 8,555 8,570	5
3. 8,570 8,585	5
4. 8,585 8,600	26
5. 8,600 8,615	18
6. 8,615 8,630	1

Построим гистограмму, откладывая по оси абсцисс интервалы l₁-l₆, а по оси ординат - отношение m_i/(n·∆l).

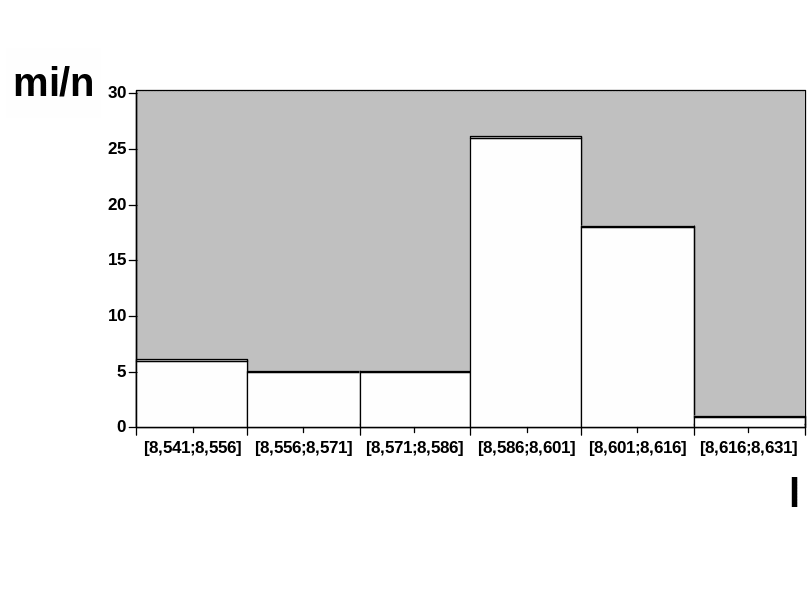
По виду представленной гистограммы можно сказать, что результат измерения подчиняется нормальному закону распределения вероятности.

Задание 2

Имеется 50 независимых числовых значений результата измерений электрического сопротивления на постоянном токе цифровым омметром с равноточными значениями отсчета (поправки внесены). Определить результат измерения силы постоянного электрического сопротивления.

Массив данных представлен пятью сериями по десять значений в каждой (n=50), Ом:

	1	2	3	4	5	6	7	8	9	10
1	119	122	124	121	123	121	119	122	119	123
2	119	121	122	122	124	122	120	122	119	124
3	123	125	122	122	121	124	126	121	126	121
4	124	125	121	121	122	122	119	123	119	122
5	125	124	119	126	119	119	123	124	121	122

Запишем значения из массива данных в возрастающем порядке в первый столбец таблицы 1, указав для каждого значения число повторений в массиве данных(второй столбец).

Таблица 1

R, Ом	m	m· R, Ом	R - , Ом	﴾R - ﴿2, Ом2	m·﴾R - ﴿2, Ом2
1	2	3	4	5	6
119	10	1190	-3	9	90
120	1	120	-2	4	4
121	9	1089	-1	1	9
122	12	1464	0	0	0
123	5	615	1	1	5
124	7	868	2	4	28
125	3	375	3	9	27
126	3	378	4	16	48

Используя результаты вспомогательных вычислений, сведенных в третий столбец таблицы 1, рассчитаем среднее арифметическое значение результата измерения:

122 Ом

Используя вспомогательные вычисления в четвертом, пятом и шестом столбцах таблицы 1, рассчитаем среднее квадратическое отклонение отдельного измерения:

2,075 Ом

Проверим массив данных на наличие промахов по «правилу трех сигм». Больше чем на 3S = 6,225 Ом от среднего арифметического значения не отличается ни одно из числовых значений результата измерения. Следовательно, можно считать, что массив данных промахов не содержит.

Строим гистограмму, откладывая по оси абсцисс значение сопротивления от R_min до R_max, разбив его на необходимое количество интервалов, а по оси ординат - отношение m_i/n.

R

Вид построенной гистограммы может свидетельствовать о том, что возможной теоретической моделью данного распределения служит нормальный закон распределения вероятности, который и примем с целью идентификации.

При количестве измерений n > 40..50 для проверки гипотезы о том, что результат измерения подчиняется нормальному закону распределения вероятности, используется критерий Пирсона.

Образуем интервалы, в каждый из которых входит не меньше 5 независимых значений результата измерения, и занесем их во второй столбец таблицы 2.

Таблица 2

i	Интервалы		mi	ti	L(ti)	Pi	mi-n·Pi
	[	]
1	2		3	4	5	6	7	8
1	(-∞;	120]	11	-0,96	-0,33147	0,16853	2,57	0,784
2	[120;	121]	9	-0,48	-0,18439	0,14708	1,65	0,370
3	[121;	122]	12	0	0	0,18439	2,78	0,838
4	[122;	123]	5	0,48	0,18439	0,18439	-4,22	1,932
5	[123;	124]	7	0,96	0,33147	0,14708	-0,35	0,017
6	[124;	125]	3	1,45	0,42647	0,095	-1,75	0,645
7	[125	+∞)	3	+∞	0,50000	0,07353	-0,68	0,126

Определим, на сколько S отстоит от среднего арифметического значения правая граница R_i каждого интервала, по формуле:

.

Полученные значения занесем в четвертый столбец таблицы 2.

По значению параметра t_i определим, с какой вероятностью отдельное значение результата измерения, подчиняющегося нормальному закону распределения вероятности, попадает в интервал . Эта вероятность определяется интегралом вероятности - функцией Лапласа L(t_i). Полученные значения L(t_i) занесем в пятый столбец таблицы 2.

Теоретическая вероятность P_i попадания в i-ый интервал отдельного значения результата измерения, подчиняющегося нормальному закону распределения вероятности, равна: .

Принимая во внимание, что L(-∞) = -0,5, а L(+∞) = 0,5, полученные расчетные значения P_i сведены в шестой столбец таблицы 2. В седьмом и восьмом столбцах приведены результаты остальных вспомогательных вычислений. Суммирование чисел в восьмом столбце дает: ² = 4,712 .

Т.к. при вероятности 0,95 равно 6,35, то рассчитанное значение ² > . Следовательно, с вероятностью 0,95 можно сказать, что ² не подчиняется ²-распределению К.Пирсона, т.е. результат измерения не подчиняется нормальному закону распределения вероятности.

Рассчитаем стандартное отклонение среднего арифметического:

0,3 Ом

Определим параметр t (коэффициент Стьюдента) при выбранной доверительной вероятности 0,95, используя уравнение Чебышева:

4,47

Рассчитаем половину ширины доверительного интервала, в котором находится результат измерения: 4,47 · 0,3 = 1,341 Ом

Результат измерения с вероятностью Р=0,95 находится в интервале:

(122 - 1,341) Ом ≤ R ≤ (122 + 1,341) Ом

120,659Ом ≤ R ≤ 123,341Ом