Министерство общего и профессионального образования

Российской Федерации

Новочеркасский государственный технический

университет

Ю. Г. Карпов, В. П. Ратауш, Е. П. Резниченко

ПРАКТИКУМ

ПО

ТЕПЛОПЕРЕДАЧЕ

Новочеркасск 1997

УДК 536.24(076.1) (076.5)

Рецензент канд. техн. наук Н.Н. Ефимов

Ю.Г. Карпов, В.П. Ратауш, Б.П. Резниченко

Практикум по теплопередаче / Карпов Ю.Г., Ратауш В.П., Резниченко Е.П.; Новочерк. гос. техн. ун-т. Новочер­касск:. НГТУ, 1997. 50 с.

Практикум по теплопередаче составлен в соответствии с программами по дисциплинам "Теоретические основы теплотехни­ки", "Тепло- и массообмен", "Термодинамика и теплопередача" и "Теплотехника". В нем содержатся задачи, предназначенные не только для закрепления теоретического курса, но и обучаю­щие методике инженерных расчетов тепловых процессов в самых различных технологических устройствах.

Практикум рекомендуется к использованию студентами всех Форм обучения при выполнении практических, самостоятельных и контрольных работ.

© Новочеркасский государственный технический универ­-

ситет. 1997

© Карпов Ю.Г., Ратауш В.П., Резниченко Е.П., 1997

Введение

Теплопередача - учение о самопроизвольных необратимых процессах распространения тепла в пространстве. Для упроще­ния анализа этот сложный процесс обмена внутренней энергией между отдельными элементами, областями рассматриваемой среды разбивают на три простейших вида теплообмена: теплопровод­ность, конвекцию и тепловое излучение.

Теплопроводностью называется перенос тепла при непосред­ственном соприкосновении тел (или частей одного тела) с раз­личной температурой.

Конвекция возможна только в жидкой среде. Под конвекцией теплоты понимают процесс ее переноса при перемещении объемов жидкости или газа в пространстве из области с одной темпера­турой в области с другой температурой. При конвекции перенос теплоты неразрывно связан с переносом самой среды.

Тепловое излучение - процесс распространения тепла с по­мощью электромагнитных волн с двойным преобразованием тепло­вой энергии в лучистую и лучистой в тепловую.

Перечисленные элементарные виды теплообмена в чистом ви­де в природе и в технике встречаются очень редко. Теплопро­водность в чистом виде встречается большей частью в твердых телах.

Совместный процесс переноса теплоты конвекцией и тепло­проводностью в жидкости называется теплоотдачей, или конвек­тивным теплообменом.

Часто встречающийся в технике процесс передачи «тепла от одной жидкости к другой через разделяющую твердую стенку на­зывается теплопередачей.

Предлагаемый сборник задач предназначен для проведения практических занятий со студентами, изучающими курс или раз­дел теплопередачи общего курса теплотехники.

Представленные задачи охватывают все основные разделы процесса теплопередачи. В каждом разделе приведены очень краткие применительно к предлагаемым задачам теоретические положения, расчетные формулы и методические указания.

Исходные данные к задачам представлены в виде таблиц по 100-вариантной системе, что обеспечивает индивидуальную работу каждого студента.

1. Теплопроводность

Процесс теплопроводности относится к простейшим видам теплообмена и представляет собой перенос тепла, осуществляемый вследствие теплового движения и энергетического взаимо­действия микрочастиц тела, обусловленного переменностью тем­пературы рассматриваемого пространства.

Согласно гипотезе Фурье, количество тепла, проходящее че­рез единицу изотермической поверхности в единицу времени, плотность теплового потока определяется уравнением

,

где  - коэффициент теплопроводности вещества, Вт/(мК); - скалярная величина градиента температуры (производная температуры t по нормали n), К/м.

Для определения скалярной величины градиента температуры чаще всего используют решение дифференциального уравнения теплопроводности, имеющего (при постоянных теплофизических свойствах материала) в декартовой системе координат вид

, (1.1)

где  - время, с; с_Р - изобарная теплоемкость вещества, Дж/(кгК);  - плотность, кг/м³; q_V - мощность внутренних источников тепла, Вт/м³.

Решением этого дифференциального уравнения для стацио­нарного теплового потока ( ) через неограниченную в двух направлениях плоскую стенку ( ) толщи­ной  в направлении оси х без внутренних источников тепла (q_V = 0) при стационарных температурах на поверхностях стен­ки t_C1 и t_C2 является линейная функция вида

Используя закон Фурье и полученное решение дифференци­ального уравнения, можно определить тепловой поток через элемент бесконечно плоской стенки поверхностью F:

Для тел цилиндрической формы решением дифференциального уравнения теплопроводности является функция

Количество теплоты, проходящее через цилиндрическую стенку, отнесенное к единице длины трубы, (линейную плот­ность теплового потока) можно определять по формуле

Тогда полный тепловой поток через цилиндрическую стенку длиной l определится как Q=q_ll.

Используя закон Ньютона-Рихмана, описывающего процесс конвективного теплообмена между поверхностью твердого тела и жидкостью, в виде

где  - коэффициент теплоотдачи, Вт/(м²К); F - поверхность теплообмена, м²; t_С, t_Ж - температуры соответственно на по­верхности твердого тела и жидкости вдали от поверхности, К, можно достаточно легко проанализировать процесс теплопереда­чи через плоские, цилиндрические однослойные и многослойные стенки. Плотность теплового потока через многослойную плос­кую стенку при граничных условиях третьего рода (заданы  и t_Ж ) определится по формуле

, (1.2)

где ₁, ₂, t_Ж1, t_Ж2 - соответственно коэффициенты теплоот­дачи и температуры жидкостей с одной и другой стороны многос­лойной стенки; _i, _i - соответственно толщины и коэффици­енты теплопроводности каждого слоя многослойной стенки; п - число слоев. Для цилиндрической стенки при аналогичных усло­виях формула для линейной плотности теплового штока имеет вид

,

где d₁, d_i, d_i+1, d_n+1 - внутренние и наружные диаметры сло-

ев многослойной цилиндрической стенки.

Применительно к однослойной плоской стенке значение

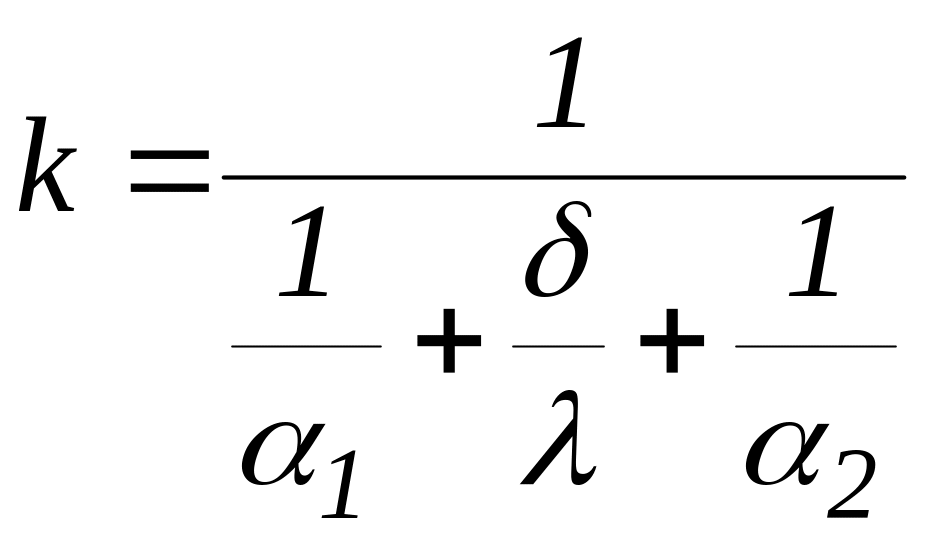
называется коэффициентом теплопередачи, Вт/(м²К), и предс­тавляет собой величину, обратную термическому сопротивлению процесса теплопередачи R, состоящему из суммы термических сопротивлений теплоотдачи с одной стороны поверхности R₁=1/₁, термического сопротивления теплопроводности стенки R₂=/ и термического сопротивления теплоотдачи с другой стороны поверхности R₃=1/₂, т.е.

R =1/k = R₁ + R₂ + R₃ = 1/₁ + / + 1/₂

В таких обозначениях формулу (1.2) можно представить в виде

Аналогичные обозначения применяют и для цилиндрических стенок:

(1.3)

где

линейный коэффициент теплопередачи, Вт/(мК); l - длина тру­бы, м.

В производственных условиях горячий теплоноситель в виде горячей воды, пара и т.д. транспортируют в трубопроводах. Для уменьшения значительных потерь тепла трубопроводы покры­вают тепловой изоляцией. Из формулы (1.3) видно, что с увели­чением толщины изоляции (т.е. с ростом d₂) термическое сопро­тивление теплопроводности R₂ = ln(d₂/d₁)/(2·) увеличива­ется, что приводит к уменьшению тепловых потерь Q, а терми­ческое сопротивление теплоотдачи R₃=1/(₂·d₂) уменьшается, что, соответственно, приводит к увеличению тепловых потерь.

Математический анализ формулы (1.3) приводит к выводу, что при d₂ меньше критического диаметра тепловой изоляции d_КР = 2·/₂ тепловые потери увеличиваются, а при d₂ > d_КР -уменьшаются. Для правильного выбора материала тепловой изоляции _ИЗ необходимо сначала рассчитать критический диа­метр тепловой изоляции. Если окажется, что величина d_КР больше наружного диаметра трубы d₁, то применение выбранного материала в качестве тепловой изоляции нецелесообразно.

Внутри объектов исследования могут быть процессы, в ре­зультате которых будет выделяться или поглощаться тепловая энергия (прохождение электрического тока, ядерные и химичес­кие реакции и т.д.).

Дифференциальное уравнение теплопроводности (1.1) для бесконечно плоской пластины с мощностью внутренних источни­ков тепла q_V, и толщиной 2, омываемой с обеих сторон жид­костью с температурой t_Ж с интенсивностью конвективного теп­лообмена, характеризуемого коэффициентом теплоотдачи , в стационарных условиях примет вид

где  - коэффициент теплопроводности материала стенки.

Решением этого дифференциального уравнения будет функция, описывающая температурное поле пластины в направлении оси X, начало координат которой расположено в центре пластины:

Количество переданного тепла пластиной с поверхностью F определиться формулой Q = 2·F··q_V.

При изучении процессов переноса тепла вдоль стержня пос­тоянного поперечного сечения, омываемого жидкостью с боковой поверхности, температура которого на одном конце поддержива­ется постоянной, необходимо обратить внимание на характер изменения температуры вдоль стержня бесконечной и конечной длины.

Для стержня бесконечной длины температурное поле вдоль направления X описывается уравнением

,

где t₁ - заданная температура на одном конце стержня; t_Ж -температура окружающей среды.

Постоянная для заданного стержня величина т

,

где  - коэффициент теплоотдачи, описывающий процесс теплооб­мена омывающей среды и стержня;  - коэффициент теплопровод­ности материала стержня; U, f - периметр и площадь поперечного сечения стержня. Аналогичная формула для стержня конечной длины l имеет вид

, (1.4)

где сh (т·l) - гиперболический косинус аргумента т·l.

Представленное решение (1.4) можно использовать для анализа погрешности измерения температуры среды при ис­пользовании гильзы в качестве оболочки, защищающей датчик от среды. Систематическая погрешность измерения

Теоретические решения этой задачи можно использовать для анализа тепловых потоков и температурных полей в реб­ристых стенках.

При передаче тепла от одной жидкости к другой через разделяющую твердую стенку определяющим является большее из всех составляющих термическое сопротивление. Для интенсифи­кации процесса теплопередачи со стороны меньшего коэффициен­та теплоотдачи устанавливают ребра, увеличивая, таким образом, поверхность теплообмена. Количество передаваемого тепла через оребренную с одной стороны плоскую стенку определяют по формуле

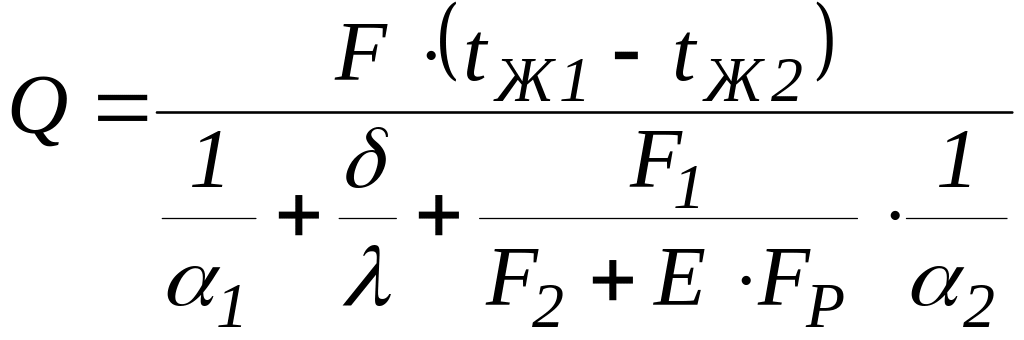
где F₁ - неоребренная (гладкая) поверхность стенки со сторо­ны первого теплоносителя, имеющего температуру t_Ж1. Интен­сивность теплообмена этого теплоносителя характеризуется коэффициентом теплоотдачи ₁; F₂ - полная поверхность стенки со стороны второго теплоносителя, имеющего температуру t_Ж2. Интенсивность теплообмена жидкости со стороны ребер определяется коэффициентом теплоотдачи ₂;  - толщина стенки без учета длины ребер;  - коэффициент теплопровод­ности стенки и ребер; Е - коэффициент эффективности ребра, учитывающий неравномерность распределения температуры вдоль ребра.

Коэффициент эффективности ребра равен отношению действи­тельного теплового потока с поверхности ребра к потоку тепла с той же поверхности при постоянной температуре ребра, рав­ной температуре у основания.

,

где th (т·l) - гиперболический тангенс аргумента т·l.

Геометрической характеристикой оребренной поверхности является коэффициент оребрения  = F₂/F₁.

Нестационарными процессами теплопроводности называют процессы, связанные с изменением температуры среды не только от точки к точке, но и с течением времени. Такие процессы наблюдаются при нагревании или охлаждении тел, помещенных в среду с заданным тепловым состоянием. Температура в каждой точке тела асимптотически приближается к температуре среды. Наиболее быстро изменяется температура точек, лежащих вблизи поверхности тела.

Теоретическое решение задач нестационарной теплопровод­ности заключается в отыскании функции, которая удовлетворяет дифференциальному уравнению теплопроводности (1.1) и усло­виям однозначности.

Для задачи охлаждения с обеих сторон плоской однородной стенки толщиной 2·, имеющей в начальный момент времени тем­пературу t₀, жидкостью с температурой t_Ж получено решение в виде бесконечного ряда

(1.5)

В последней формуле параметр ₁, ₂, ….. определяется из тригонометрического уравнения сt(_i)=_i/Bi. Это, уравнение имеет бесконечное множество решений i = 1,2,3,...,.

Число Био Bi = / определяется геометрическим размером пластины , коэффициентом теплопроводности материала стенки  и коэффициентом теплоотдачи , характеризующим процесс теплового взаимодействия поверхностей стенки с жидкостью. Число Фурье Fо = а/², где а - коэффициент температуропро­водности, м²/с;  - время, с.

Полученная формула неудобна для ручного счета, т.к. тре­бует геометрического (или на ЭВМ) определения корней три­гонометрического уравнения. Для инженерных расчетов чаще всего требуется определение температуры в центре и на по­верхности пластины. В этом случае удобнее использовать но­мограммы, построенные для тел простой формы (пластина, ци­линдр, шар, полый цилиндр, параллелепипед и т.д.) по форму­лам (1.5) и аналогичным ей. Эти номограммы имеют вид рис.1.

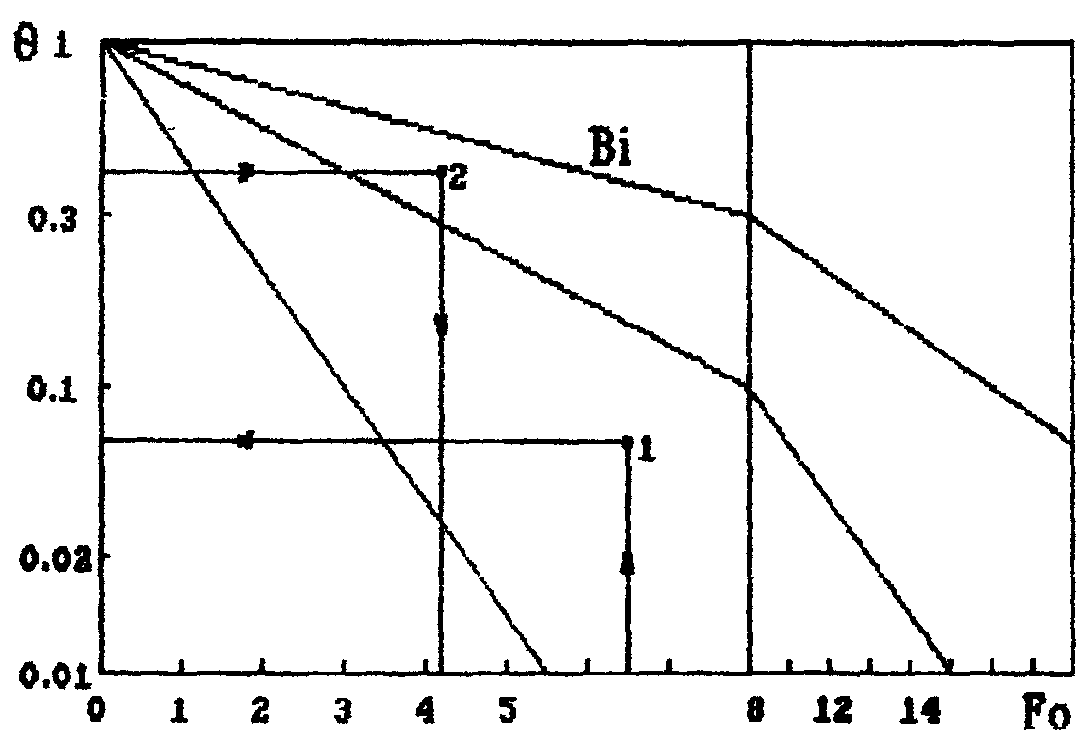
Рис. 1

Безразмерная температура  = (t – t_Ж)/(t₀ – t_Ж). Для того, чтобы определить температуру в центре или на поверхности (для центра и поверхности имеются свои номограммы ), необходимо:

а) определить для заданных условий числа Bi и Fо;

б) по номограмме (точка 1) определить ;

в) искомую температуру найти по формуле

t = t_Ж +  (t₀ – t_Ж)

При помощи этих номограмм можно решать и обратные задачи. Например: определить, через какой промежуток времени темпера­тура в центре (на поверхности) примет заданное значение t. Решение этой задачи необходимо производить в следующей пос­ледовательности:

а) определить для заданных условий число Bi;

б) определить безразмерную температуру ;

в) по номограмме определить точку 2 и значение числа Fо;

г) по найденному численному значению Fо определить искомое время =Fo²/a .