Использование критерия Стьюдента.

Получение большого количества точек для построения кривой распределения требует проведения многократных измерений с большим числом образцов. В связи с этим нередко ограничиваются небольшим числом наблюдений (образцов), стремясь получить оценочное значение параметра с достаточной для практики точностью. С помощью критерия Стьюдента удается при ограниченном числе наблюдений (так называемой частичной совокупности ) установить с определенной степенью вероятности границы, между которыми заключено среднее значение искомого параметра , отвечающее полной совокупности (т.е. достаточно большому числу) опытов.

Рассмотрим последовательность статистической обработки результатов измерения, например диэлектрической проницаемости ε.

В результате экспериментов получили частичную совокупность значений εi. Находят среднее значение частичной совокупности

Εчаст=(1/N)Σεi

Где N–число наблюдений. Вместо определения среднего квадратичного отклонения , которое для частичной совокупности неизвестно, производят оценку этого отклонения по формуле

S=[Σ(ε_i-ε_част)²/(N-1)]^1/2

Границы, заключающие среднеe значение полной совокупности ε_ср, согласно критерию Стьюдента определяются величинами

ε=ε_част±St(γ)/(N)^1/2

Их часто называют доверительными границами при доверительной вероятности ( γ ).

Здесь t(γ) – табличная функция вероятности γ и количества наблюдений N. Значение доверительной вероятности обычно задается равным 0,95-0,999.

Чем больше число наблюдений, тем ближе друг к другу границы, т.е. тем больше точность определения ε_ср.

Рассмотрим применение критерия Стьюдента на примере определения диэлектрической проницаемости текстолита по данным 10 измерений при доверительной вероятности 0,95. Оказалось, что значение ε колеблется от 4,7 до 5,5. Сумма всех измеренных значений ε Σε=50,3. Далее подсчитываем

ε_част=50,3/10=5,03

S=(1,282/9)^1/2=0,377

В таблице находит для γ=0,95 и N=9 t=2.26. Подставляя полученные величины, находим

S/(10)^1/2 =0,269.

Граничные значения ε_ср=5,03±0,27

Таким образом, с вероятностью 95% можно утверждать, что величина ε_ср ограничена значениями

4,76≤ ε_ср ≤ 5,30

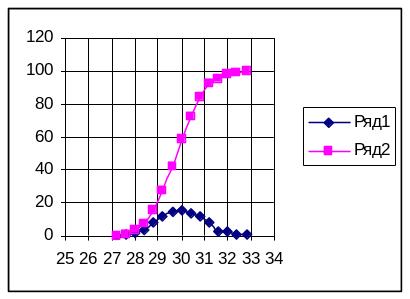
Результаты определения электрической прочности

№ интервала	Напряжение пробоя	р	М Общее число пробоев	Ui-Ucp	(Ui-Ucp)2
1	27,2	0,3	0,3	3.04	9.25
2	27,6	1	1,3	2.64	6,97
3	28	2,0	3,3	2.24	5,00
4	28,4	4,0	7,3	1.84	3,38
5	28,8	8,5	15,8	1.44	2,07
6	29,2	12,0	27,8	1.04	1,08
7	29,6	14,5	42,3	0.64	0,41
8	30	16	58,3	0.24	0,06
9	30,4	14	72,3	0.16	0,013
10	30,8	12	84,3	0.56	0,31
11	31,2	8	92,3	0.96	0,92
12	31,6	3	95,3	1.36	1,85
13	32	3	98,3	1.76	3,04
14	32,4	1	99,3	2.16	4,67
15	32,8	0,7	100	2.56	6,55
Сумма	Uср=30,24	100

σ=0,676 кВ

kвар=2,24%

Оценка расхождений между средними знпчениями

Проверим гипотезу, что две независимые частичные совокупности n₁ и n₂ взяты из одной и той же нормально распределенной общей совокупности, имеющей среднее значение X₀ и дисперсию ² .

Пусть оценки дисперсии S₁ и S₂ и пусть проверяемая гипотеза верна. Основой проверки является разность X_cp1 и X_cp2 , дисперсия которой равна

₁²/n₁+₂²/n₂ = (n₁ + n₂ )² /n₁n₂

Так как оценки S₁² и S₂² дисперсии ² имеют вес n₁ -1 и n₂ -1, то полная оценка дисперсии ² будет равна

S² =[(n₁ -1)S₁² +(n₂ -1)S₂²]/[(n₁ -1)+(n₂ -1)] =

= [(X-X_cp)² +(X-X_cp)²]/(n₁ +n₂ -2)

В результате получаем

t = [(X -X_cp1)²/S][n₁n₂ /(n₁ +n₂ )]

Для оценки значимости расхождения между двумя средними можно воспользоваться таблицей t с числом степеней свободы n₁+n₂ -2.

В вышеприведенном примере t=2,8, а табличное t=2,567 при =18 P=0,02. Т.о. вероятность случайных значений t, которые по абсолютной величине не меньше наблюдаемого t ничтожно мала. Следовательно, наблюдаемое расхождение не является случайным.

Оценка дисперсии. Критерий Фишера.

Пусть есть две независимых совокупности X'...X_n1 ' и X"...X_n2 " со средними значениями X_cp1 и X_cp2 . Оценки дисперсий S₁² и S₂² .Необходимо выяснить, являются ли эти оценки существенно pазличными или данные частичные совокупности можно рассматривать, как взятые наудачу из нормальных общих совокупностей, имеющих равные дисперсии ² .

Для решения этой задачи используют критерий Фишера F - (дисперсионное отношение) - отношение оценок S₁² и S₂² дисперсии  , полученные из независимых частичных совокупностей F=S₁²/S₂² . Построены таблицы F в зависимости от степени свободы , которые могут быть превзойдены соответственно с вероятностью 0,05; 0,01 и др.

Проверяемая гипотеза: Частичные совокупности взяты из одной и той же совокупности из нормальных общих совокупностей равной дисперсией. За S₁² берется большая из них.

- - - - - - - - - - - - - - - - - - - - - - -- - - - - - - - - - - -

Пример. 4. Пусть работают два лаборанта. У одного из них получилось X_ср1 =4,57 S₁² =0,0295 =19 (n=20). У другого X_ср2 =4,56 S₂²=0,0139 =12

Находим F=0,0295/0,0139=2,12. По таблице при =19 и 12 и 5% уровне значимости F=2,54. Так как рассчитанное F меньше табличного, то нет оснований считать разницу в точности существенной.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Критерий Романовского

Для сравнения дисперсий с помощью критерия Романовского вводится величина f=[(n -2)/n ]F, где F-критерий Фишера. Математическое ожидание этой величины в случае независимого выбора из нормальных общих совокупностей с одинаковой дисперсией равно 1, а основное отклонение равно _r =+[(2₁ +₁ -2)/ ₁(₂ -4)]^1/2 .

По величине критерия R=|f-1|/_r можно сделать заключение о существенности или случайности расхождений между оценками S₁² и S₂² .

Если R3, то расхождение существенно.

Если R<3, то расхождение признается случайным.

Для применения этого критерия надо, чтобы одно из значений степеней свободы было больше 4. Оно принимается за ₂ . В примеpе о работе двух лаборантов получаем f=1,77 и _r =0,72 R=1,07.Вывод тот же.

Критерий согласия Пирсона P(² )

Критерий Пирсона проверяет гипотезу, удовлетворяет ли рассматриваемая случайная величина заданному закону распределения F(X). Критерий Пирсона называется также критерием согласия или критерий хи-квадрат. Критерий служит для проверки гипотезы, что функция распределения, полученная экспериментально, F(X), соответствует некоторой заданной (гипотетической) функции распределения F₀(X). Для расчетов область значений Х делится на ряд интервалов h. Пусть р_i теоретическая вероятность того, что случайная величина попадает в интервал i. Затем сравниваем число с теоретическим.

Распределение Р(²) представляет собой вероятность того, что

случайная величина ² =(X_h²/_h² ) (где X_h =n_i -n_ч ; n_ч -частота нормального распределения) примет значение, превосходящее некоторое заданное :

_h

² =(n_i-np_i)²/np_i

ⁱ⁼¹

где р_i=n_i/n и h-число интервалов; X_h(h=1,n) - независимые случайные величины, имеющие нормальные распределения с общим средним значением, равным нулю и дисперсиями _h² (h=1,n). Число независимых величин  - число степеней свободы.

Пусть есть m независимых линейных связей и n - случайные величины.

Тогда =n-m. Есть Таблица, где по данному значению ² и числу степеней свободы  n найти вероятность P(²) того, что ² превзойдет данное значение.

Например, для n=10 и 5% уровня значимости по таблице находим ² =18,307. Это значит, что вероятность того, что ² с 10 степенями свободы будет превышать 18,307, равна 0.05. Когда n>30 вероятность P(²) находится по формуле

P(²)=(1/2)[1-Ф(x)],

где Ф(X) берется из таблицы - функция Лапласа.

При >30, распределение величины (2² )^1/2 оказывается приближенно нормальным со средним значением, равным (2-1)^1/2 и основным отклонением, равным единице.

Оценка воспроизводимости.

Дисперсию генеральной совокупности ²_х нормально распределенной случайной величины можно оценить, если известно распределение ее оценки - выборочной дисперсии S²_ч . Распределение S²_х можно получить по распределению ² .

Если есть выборка n независимых наблюдений X₁ ,X₂ ,...X_n над нормально распределенной случайной величиной, то имеет место распределение ²

² =[(X_i -X_cp)² /_х ]

с f=n-1 степенями свободы. Плотность ² зависит только от f:

f(²)= 1/[2^f/2 Г(f/2)] (²)^(f-2)/2 exp(-² /2), 0 <  < .

Есть таблицы f от f и с разной 1-p доверительной вероятностью.

Двусторонняя оценка S_x. Кривые асимметричны, степень симметрии

уменьшается с увеличением f.

² _p/2 ² ² _1-p/2

Односторонняя оценка: ²  ²_1-p ; ²  ²_p .

Или двусторонняя:

fS²_x / ² _1-p/2  ²_х  fS²_х/²_р

и односторонняя:

_х²  fS_х² /² _р и _х²  fS_х² /²_1-р

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Пример 5. Испытания показали,что параметр X равен 17,2, 16,3, 15,5

Определить ошибку воспроизводимости. Для этого рассчитаем выборочную дисперсию

S_х² = (X-X_ср)² /(3-2)=0,73

При доверительной вероятности 1-р=0,9 по таблице при f=2 находим

² _0,05 =6 и ² _0,95 = 0,103

0,73 х 2/6  _х²  0,73 х 6/0,103

0,24  _х²  14,1

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

При n>30 выборочная S распределена нормально с математическим ожиданием  с ощибкой _s = _x /(2f)^1/2 = S_x/(2f)^1/2

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Пример 6. Оценить ошибку воспроизводимости s для выборки из 31

измерений с S =0,85 при 1-p = 0,9.

Доверительный интервал:

² _0,05 = 43,8 и ² _0,95 =18,5

0,85 .30/43,8  _х²  0,85.30/18,5; 0,48  _х²  1,13

Ошибки косвенных измерений

Пусть случайная величина Z зависит от наблюдений по известному

закону Z=f(X₁ ,X₂ ,...X_n ). Дисперсию косвенных измерений можно найти, зная дисперсию отдельных наблюдений. На практике определяют выборочную дисперсию S_xi² и по ним выборочную дисперсию косвенного измерения S_z² . Чтобы найти ее, разложим функцию Z(X) в ряд Тейлора в точке m₁ ,m₂...m_n , ограничиваясь членами первого порядка:

Z=f(m₁ , m₂ ...m_n ) + (X₁ -m₁ )df/dX₁ + (X₂ -m₂ )df/dX₂ +...(X_n -m_n )df/dX_n

и S_z определим по закону сложения дисперсий (закон накопления ошибок)

_n

S_z² = (df/dX_i )S_i²

ⁱ⁼¹

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Пример 7. Определить ошибку определения линейной скорости движения газа в трубопроводе v, если измерено G=3000 м /час, S =10 м /час, сечение трубопровода F=0,1 м  1 см .

Решение: v - результат косвенных измерений v=G/F=3000/0,1=30000 м/час= =8,82 м/сек. S_v =[(dv/dG)² S_G² + (dv/dF)² S_F² ]^1/2 = [S_G²/F² + G² S_F²/F⁴]^1/2 =

= [10000 + 900]^1/2 = 100/3600 = 0,03 м/c

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Определение воспроизводимости (дисперсии по текущим измерениям).

Если сделано m параллельных опытов и получена выборка y₁ ,y₂ ,...y_n то дисперсия воспроизводимости

_u

S_в² =[(y-y_cp)]/(m-1)

^u-1

и ошибка опыта (ошибка воспроизводимости ) S_вос = (S_в²)^1/2

Общая дисперсия воспроизводимости S² = (y_n -y_i)/m_i -n

где y_n =y_m /m_m.

Если число параллельных опытов одинаково (m₁ =m₂ =...=m),то дисперсия воспроизводимости S² =S_i²/n или

_{n m}

S_в² =  (y_iu-y_icp)²/n(m-1)

^{i-1 u-1}

Если выборочные дисперсии получены по выборкам одинаковых объемов m₁=m_n=...=m , то для их сравнения используют критерий Кохрена

_n

G=S²_max /S_i²

ⁱ⁼¹