114. Організація комп'ютерних систем із розподіленою пам'яттю

Системи передачі повідомлень - клас багатопроцесорних систем, в яких кожен про­цесор має доступ до своєї локальної пам’яті. На відміну від систем із спільною пам’яттю, комунікації в системі передачі повідомлень виконуються шляхом посилання та отриман­ня повідомлень. Вузол в такій системі складається з процесора і його локальної пам’яті (рис. 12.22).

Рис. 12.22. Система з розподіленою пам’яттю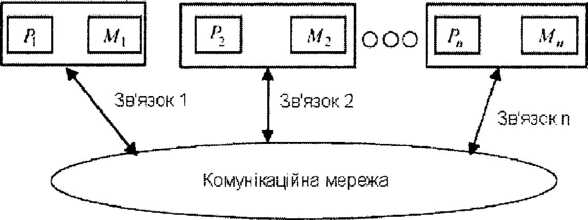

Вузли зазвичай запам’ятовують повідомлення в буферах (тимчасові комірки пам’яті, де повідомлення чекають до того часу, коли вони можуть бути послані або одержані), і виконують посилання-отримання повідомлення під час обробки даних. Паралельна об­робка повідомлення і поточного обчислення здійснюється під керуванням операційної системи. Процесори не розділяють спільну пам’ять і кожен процесор має доступ до його власного адресного простору. Вузли в системі передачі повідомлень можуть бути з’єдна­ні різноманітними способами - від спеціалізованих комутаторів до географічно розпо­ділених мереж.

Підхід передачі повідомлень є масштабованим до великих пропорцій, тобто число процесорів може бути збільшено без істотного зменшення ефективності їх взаємодії.

Для організації зв’язку системи передачі повідомлень використовують статичні ме­режі, зокрема гіперкубічні мережі, які були досить популярні протягом багатьох років. Двовимірні і тривимірні решітчасті мережі так само широко використовувались в сис­темах передачі повідомлень. Два важливі чинники повинні розглядатися в проектуван­ні комунікаційної мережі для систем передачі повідомлень. Це - пропускна здатність і мережний час очікування. Пропускна здатність визначена як кількість бітів інформації, переданих за одиницю часу (біт/сек). Мережний час очікування визначений як час, по­трібний для передачі повідомлення. В 1987 році була введена блокова маршрутизація як альтернатива традиційній маршрутизації з проміжним зберіганням для того, щоб скоротити розмір необхідних буферів і щоб зменшити час очікування повідомлення. У блоковій маршрутизації пакет ділиться на менші блоки, які називають блоками керу­вання потоком даних, так, що ці блоки рухаються конвеєрним методом разом з блоком заголовка до вузла призначення. Коли блок заголовка блокується через мережний затор, наступні за ним блоки блокуються також.

115. Комунікаційні мережі багатопроцесорних систем

Типи комунікаційних мереж

В основі архітектури будь-якої багатопроцесорної комп’ютерної системи лежить здатність до обміну даними між її компонентами. Це забезпечується комунікаційною мережею (КММ), яка з’єднує між собою вузли комп’ютерної системи за допомогою ка­налів передачі даних (каналів зв’язку). В ролі вузлів можуть виступати процесори, мо­дулі пам’яті, пристрої введення-виведення, комутатори або декілька перерахованих елементів, об’єднаних у функціональний пристрій. Організація внутрішніх комунікацій комп’ютерної системи називається топологією.

Топологію комунікаційної мережі визначає множина вузлів, які об’єднані множи­ною каналів. Зв’язок між вузлами зазвичай реалізується по двоточковій схемі (point-to- point). Будь-які два вузли, зв’язані каналом зв’язку, називають суміжними вузлами або сусідами. Кожен канал з’єднує один вузол-джерело з одним вузлом-приймачем. Канал характеризується кількістю сигнальних ліній, частотою або швидкістю передачі бітів по кожній сигнальній лінії, затримкою - часом пересилання біта з одного вузла до іншого. Для більшості каналів затримка знаходиться в прямій залежності від фізичної довжини лінії зв’язку та швидкості розповсюдження сигналу.

Вузол у мережі може бути термінальним, тобто джерелом або приймачем даних, ко­мутатором, що пересилає інформацію з вхідного порту на вихідний, або суміщати оби­дві ролі. У мережах із прямими зв’язками кожен вузол одночасно є як термінальним вузлом, так і комутатором, і повідомлення пересилаються між термінальними вузлами безпосередньо. У мережах з непрямими зв’язками вузол може бути або термінальним, або комутатором, але не одночасно, тому повідомлення передаються опосередковано, за допомогою виділених комутуючих вузлів. Існують також такі топології, які не можна однозначно зарахувати ні до прямих, ні до непрямих. Будь-яку пряму КММ можна зо­бразити у вигляді непрямої, розділивши кожен вузол на двотермінальний вузол і ву­зол комутації. Сучасні прямі мережі реалізуються саме таким чином - комутатор від­діляється від термінального вузла і поміщається у виділений маршрутизатор. Основна перевага прямих КММ полягає в тому, що комутатор може використовувати ресурси термінальної частини свого вузла. Це стає істотним, якщо врахувати, що, як правило, останній включає комп’ютер або процесор.

Комунікаційні мережі багатопроцесорних систем можуть бути поділені на наступні групи:

• залежно від того, чи залишається конфігурація взаємозв’язків незмінною, при­наймні поки виконується певне завдання, розрізняють мережі із статичною і динаміч­ною топологіями;

• залежно від способу функціонування: синхронні та асинхронні;

• залежно від стратегії керування: централізовані та децентралізовані;

• залежно від способу перемикання: схемні та пакетні.

З’єднання в статичній мережі є фіксованими, тоді як в динамічній мережі вони мо­жуть змінюватися в процесі роботи мережі за допомогою програмних засобів. При цьому статичні комунікаційні мережі в свою чергу ділять на одно-, двовимірні та гіперкубічні.

Динамічні комунікаційні мережі ділять на шинні (одно та багатошинні) та комутую­чі (одноярусні, багатоярусні та координатні), як це показано на рис. 12.23.

Рис. 12.23. Топології комунікаційних мереж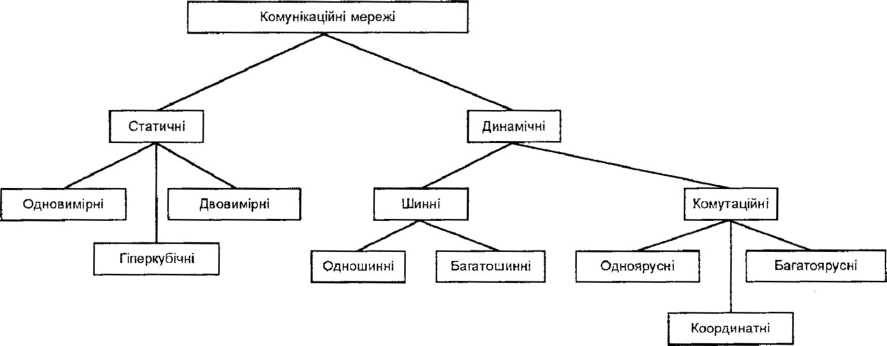

Дві можливі стратегії операцій взаємодії в мережі - це синхронна й асинхронна. У синхронних КММ всі дії жорстко узгоджені в часі, що забезпечується за рахунок єди­ного генератора тактових імпульсів (ГТІ), сигнали якого одночасно транслюються у всі вузли. В асинхронних мережах єдиного генератора немає, а функції синхронізації роз­поділені по всій системі, причому в різних частинах мережі часто використовуються ло­кальні ГТІ.

Залежно від вибраної стратегії комутації розрізняють мережі з комутацією з’єднань і мережі з комутацією пакетів. Як у першому, так і в другому варіанті інформація переси­лається у вигляді пакету. Пакет є групою бітів, для позначення якої застосовують також термін повідомлення.

У мережах з комутацією з’єднань шляхом відповідного встановлення комутуючих елементів мережі формується канал від вузла-джерела до вузла-приймача, що зберіга­ється, поки весь пакет не досягне пункту призначення. Пересилання повідомлень між певною парою вузлів проводиться завжди поодинці і за тим же маршрутом.

В мережі з комутацією пакетів приймається, що повідомлення самостійно знаходить свій шлях до місця призначення. На відміну від мереж із комутацією з’єднань, маршрут від початкового пункту до пункту призначення кожного разу може бути іншим. Пакет послідовно проходить через вузли мережі. Черговий вузол запам’ятовує прийнятий па­кет у своєму буфері тимчасового зберігання, аналізує його і робить висновки, що з ним робити далі. Залежно від завантаженості мережі ухвалюється рішення про можливість негайного пересилання пакету до наступного вузла і про подальший маршрут прохо­дження пакету на шляху до пункту призначення. Якщо всі можливі канали для пере­міщення пакету до чергового вузла зайняті, в буфері вузла формується черга пакетів, яка “розсмоктується” у міру звільнення ліній зв’язку між вузлами (якщо черга також на­сичується, то відповідно до однієї із стратегій маршрутизації може відбутися так зване “скидання хвоста”, тобто відмова від пакетів, що знову поступають).

КММ можна також класифікувати по тому, як в них організоване керування. У де­яких мережах, особливо з комутацією з’єднань, прийняте централізоване керування (рис.12.24).

Рис.12.24. Багатопроцесорна система на основі комунікаційної мережі з централізованим керуванням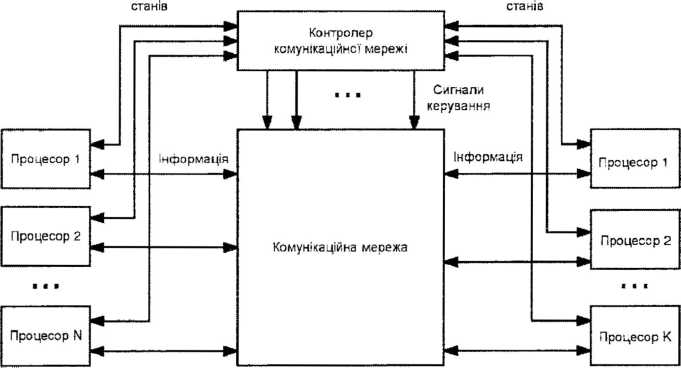

Процесори посилають запит на обслуговування в контролер комунікаційної мережі, який проводить арбітраж запитів із врахуванням заданих пріоритетів, і встановлює по­трібний маршрут. До даного типу слід віднести мережі з шинною топологією. Процесор­ні матриці також будуються як мережі з централізованим керуванням, яке здійснюється сигналами від центрального процесора. Приведена схема застосовна і до мереж з ко­мутацією пакетів. Тут тег маршрутизації, що зберігається в заголовку пакету, визначає адресу вузла призначення. Більшість серійних комп’ютерних систем має саме цей тип керування.

У схемах із децентралізованим керуванням функції керування розподілені по вузлах мережі. Варіант із централізованим керуванням простіше реалізується, але розширення мережі в цьому випадку пов’язане із значними труднощами. Децентралізовані мережі в плані підключення додаткових вузлів є значно гнучкішими, проте взаємодія вузлів у таких мережах є істотно складнішою.

У ряді мереж зв’язок між вузлами забезпечується за допомогою деякої множини ко­мутаторів, але існують також мережі з одним комутатором. Наявність великого числа комутаторів веде до збільшення часу передачі повідомлення, але дозволяє використову­вати прості комутуючі елементи. Подібні мережі зазвичай будують як багатоярусні.

Основні характеристики комунікаційних мереж багатопроцесорних систем

До основних характеристики комунікаційних мереж багатопроцесорних систем на­лежать наступні:

• розмір;

• складність;

• кількість зв’язків;

• діаметр;

• затримка;

• частота роботи;

• пропускна здатність;

• здатність до розширення;

• надійність.

Розмір мережі визначається кількістю вузлів, які об’єднані мережею.

Складність мережі вимірюється кількістю обладнання, потрібного для її реалізації. При цьому одиницею вимірювання може бути транзистор, вентиль або вузол деякої приведеної складності, наприклад, двовходовий мультиплексор.

Важливою характеристикою мережі є кількість зв’язків (каналів) між вузлами мере­жі, яка суттєво впливає на складність мережі та її надійність.

Діаметр мережі - число вузлів, через які повинне пройти повідомлення, щоб досягти його місця призначення.

З діаметром тісно пов’язана інша характеристика мережі - затримка, яка рівна часу проходження повідомлення через вузли мережі до місця призначення.

Частота роботи мережі визначає, як швидко дані можуть передаватися через мережу одне за одним.

Із частотою та кількістю зв’язків мережі тісно пов’язана пропускна здатність мережі, тобто кількість інформації, яка може бути передана через мережу за одиницю часу.

Важливою характеристикою мережі є її здатність до розширення шляхом додавання додаткових вузлів. Вартість додавання вузла залежить в значній мірі від кількості компо­нентів і зв’язків, потрібних для додавання вузла. Для деяких мереж вартість додавання вузла фіксована. Причому, для одних мереж вартість додавання вузлів зростає лінійно або квадратично як функція розміру мережі, для інших - логарифмічно. Вартість часто є обмежуючим чинником для розширення даної мережної топології.

Надійність в значній мірі залежить від надлишковості мережі, яка визначається кіль­кістю різних шляхів, через які повідомлення може пройти від його джерела до місця призначення. Якщо немає ніякої надлишковості, дефектний вузол може зашкодити про­ходженню всіх або частини повідомлень через нього, та досягненню їх місць призна­чення. Надлишкова мережа не тільки більш пристосована до дефектів компонентів, але також забезпечує зміну напрямів пересилання повідомлень, і таким чином полегшує ви­рішення питань блокування в мережі.

Статичні топології комунікаційних мереж багатопроцесорних систем

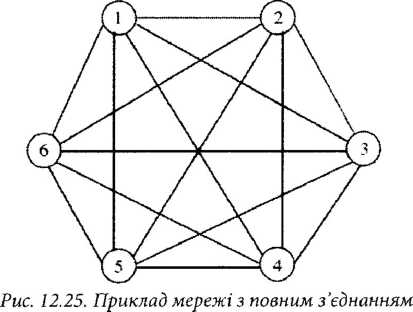
Статичні (фіксовані) комунікаційні мережі мають однонаправлені та двонаправлені фіксовані канали зв’язку між процесорами. Може бути виділено два види статичних ме­реж. Це мережі з повним з’єднанням (CCN - completely connected networks) та мережі з обмеженим з’єднанням (LCN - limited connection networks).

У мережі з повним з’єднанням (повнозв’язних мережах) кожен вузол з’єднаний зі всіма іншими вузлами у мережі. Мережа з повним з’єднанням гарантує швидку достав­ку повідомлення від будь-якого початкового вузла до будь-якого вузла призначення, оскільки йому доведеться перетнути лише один канал зв’язку. Так як кожен вузол з’єд­наний з кожним іншим вузлом в мережі, організація обміну повідомленнями між вузла­ми стає простим завданням. Мережі з повним з’єднанням є, проте, дорогими, оскільки вимагають великої кількості каналів зв’язку для їх побудови. Ця незручність стає оче­видною при великих кількостях вузлів N. Слід зазначити, що число каналів зв’язку в мережі з повним з’єднанням рівне N(N-l)/2, тобто асимптотична складність цієї мережі, виражена кількістю каналів зв’язку, є 0(N²). Часова затримка мережі з повним з’єднан­ням, виражена кількістю пересічених зв’язків, є постійною і рівною 1. Мережа з повним з’єднанням, приведена в якості прикладу на рис. 12.25, має N = 6 вузлів. Як результат, для 'їх з’єднання потрібно 15 каналів зв’язку.

Мережі з обмеженим з’єднанням не забезпечують безпосереднього зв’язку кожно­го вузла з кожним іншим вузлом мережі. Натомість, комунікації між деякими вузлами мають бути здійснені через інші вузли мережі. Довжина шляху між вузлами, виміряна кількістю каналів зв’язку, які доведеться перетнути, є довшою, порівняно з випадком мереж з повним з’єднанням. Крім того, при застосуванні мереж з обмеженим з’єднанням виникає ще дві інших проблеми. Це потреба пошуку ефективної топології комунікацій­ної мережі і потреба в механізмі маршрутизації повідомлень по мережі, поки вони не досягають своїх місць призначення.

Нижче ці дві проблеми обговорюється детальніше.

З розвитком архітектури кОіМп’ютерів створено цілий ряд топологій комунікаційних мереж з обмеженим з’єднанням. Ці топології включають:

• одновимірні (лінійні) топології;

• двовимірні топології (кільце, зірка, дерево, решітка);

• тривимірні топології (повнозв’язна топологія, кубічна топологія, гіперкубічні то­пології).

Прості приклади цих топологій комунікаційних мереж показані на рис. 12.26.

У лінійній топології вузли комунікаційної мережі утворюють одновимірний масив 5 (рис. 12.26 а), в якому кожен вузол з’єднаний з своїми двома безпосередніми сусідні­ми вузлами. Два вузли в кінцях масиву з’єднані з своїм єдиним безпосереднім сусідом. Якщо вузлу і потрібно зв’язатися з вузлом), де^>і, то повідомленню від вузла і доводить- З ся перетнути вузли і+1, і+2,...,;'-і. Так само, коли вузлу і потрібно зв’язатися з вузлом), де З і>^, то повідомлення від вузла і має перетнути вузли і-1, і-2,..., і-]. У найгіршому випадку, З коли вузлу 1 доводиться відправити повідомлення вузлу X, повідомленню доведеться З перетнути в сумі N-1 вузлів, щоб досягти свого місця призначення. Тому, хоча ліній- з ні масиви є простими і мають прості механізми маршрутизації, вони є повільними. Це З особливо відчувається, коли число вузлів N велике. Мережна асимптотична складність = лінійного масиву є О(М) і його часова асимптотична складність є О(Х).

Якщо обидва вузли в кінцях лінійної мережі з’єднати, отримається мережа з струк- З турою кільця (рис. 12.26 Ь). Вона може бути однонаправленою та двонаправленою, за- з лежно від кількості каналів зв’язку та напрямку передачі в них даних. Прикладом сис- З тем, в яких використано топологію кільця, є мережа Токеп Яп^ та система БСІ.

Решітчаста (сотова) топологія комунікаційної мережі (рис. 12.26 с) в загальному є п-вимірною матрицею, яка має К₀хК х...хК_п, вузлів, де п - число вимірів мережі, і Кі є з основа виміру і. Існує велика кількість сотових мереж, які відрізняються з’єднаннями вузлів. Наприклад, на рис. 12.26 сі показана сотово-кільцева мережа, в якій крайні вузли замкнуті в кільце. Рис. 12.27 показує приклад сотової мережі розміром 3x3x2. Вузол, по­зиція якого є (і, і, к), з’єднаний із своїми сусідами з позицією і+1, і+1, ік+1. Потрібно від значити, що для сотової мережі з N вузлами найдовша відстань між двома довільними вузлами пропорційна К^|й, тобто її часова асимптотична складність є 0(ІЧ^тШ).

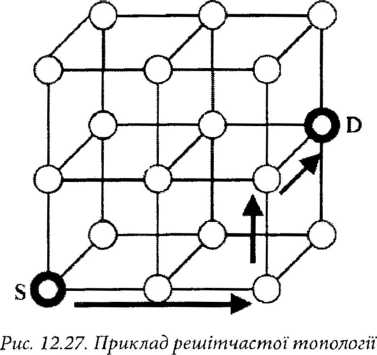Багатопроцесорні комп’ютерні системи з сотовою топологією комунікаційної мережі є ефективними для виконання наукових обчислень. Іншою перевагою сотових мереж є те, що вони масштабуються. Велика матриця може бути отримана з малої без зміни по­рядку вузла (кількості входів). Тому багато комп’ютерних систем з розподіленою пам’ят­тю У лінійній топології вузли комунікаційної мережі утворюють одновимірний масив 5 (рис. 12.26 а), в якому кожен вузол з’єднаний з своїми двома безпосередніми сусідні­ми вузлами. Два вузли в кінцях масиву з’єднані з своїм єдиним безпосереднім сусідом. Якщо вузлу і потрібно зв’язатися з вузлом), де^>і, то повідомленню від вузла і доводить- З ся перетнути вузли і+1, і+2,...,;'-і. Так само, коли вузлу і потрібно зв’язатися з вузлом), де З і>^, то повідомлення від вузла і має перетнути вузли і-1, і-2,..., і-]. У найгіршому випадку, З коли вузлу 1 доводиться відправити повідомлення вузлу X, повідомленню доведеться З перетнути в сумі N-1 вузлів, щоб досягти свого місця призначення. Тому, хоча ліній- з ні масиви є простими і мають прості механізми маршрутизації, вони є повільними. Це З особливо відчувається, коли число вузлів N велике. Мережна асимптотична складність = лінійного масиву є О(М) і його часова асимптотична складність є О(Х).

Якщо обидва вузли в кінцях лінійної мережі з’єднати, отримається мережа з струк- З турою кільця (рис. 12.26 Ь). Вона може бути однонаправленою та двонаправленою, за- з лежно від кількості каналів зв’язку та напрямку передачі в них даних. Прикладом сис- З тем, в яких використано топологію кільця, є мережа Токеп Яп^ та система БСІ.

Решітчаста (сотова) топологія комунікаційної мережі (рис. 12.26 с) в загальному є п-вимірною матрицею, яка має К₀хК х...хК_п, вузлів, де п - число вимірів мережі, і Кі є з основа виміру і. Існує велика кількість сотових мереж, які відрізняються з’єднаннями вузлів. Наприклад, на рис. 12.26 сі показана сотово-кільцева мережа, в якій крайні вузли замкнуті в кільце. Рис. 12.27 показує приклад сотової мережі розміром 3x3x2. Вузол, по­зиція якого є (і, і, к), з’єднаний із своїми сусідами з позицією і+1, і+1, ік+1. Потрібно від-базуються на таких мережах, наприклад система МРР фірми Goodyear Aerospace, сис­тема Paragon фірми Intel, система J-Machine Масачусетського технологічного інституту.

Зіркоподібна топологія (рис. 12.26 е) передбачає об’єднання багатьох вузлів через один центральний вузол і характеризується простотою організації керування.

В деревовидній мережі, в якій двійкове дерево, показане на рис. 12.26 f, є частковим випадком, якщо вузлу на рівні і (коренева вершина знаходиться на рівні 0) потрібно зв’я­затися з вузлом на рівні], де i>j і вузол призначення належить піддереву того ж кореня, то йому доведеться направити повідомлення вгору через прохідні вузли рівнів і—1, і-2,..., j+1, поки воно не досягне вузла призначення. Якщо вузлу на рівні і потрібно зв’язатися з іншим вузлом на тому ж рівні і (або з вузлом на рівні j ф і, де вузол призначення нале­жить піддереву іншого кореня), йому доведеться направити повідомлення вгору дерева, поки повідомлення не досягає вершини на рівні 0. Після цього повідомлення доведеться направити вниз від вершини, поки воно не досягне місця призначення. Слід зазначити, що кількість вузлів в мережі двійкового дерева, що має k рівнів, рівна N(k) = 2* - 1.

Максимальна глибина мережі двійкового дерева рівна log₂N, де N - число вузлів в мережі. Тому, апаратна асимптотична складність цієї мережі є 0(2^к) і її часова асимпто­тична складність є 0(log₂ N).

Досить популярними є кубічні (рис. 12.26 g) та гіперкубічні топології, які дозволяють зменшити часову складність статичних топологій мереж.

Гіперкубічні мережі мають структуру n-мірного куба, n-мірний куб (гіперкуб поряд­ку п) визначають як неорієнтований граф, що має 2" мічених вершин від 0 до 2“"^!, в якому є дуга між заданою парою вершин лише в тому випадку, якщо двійкове представлення їх адрес відрізняється лише одним бітогА. Як приклад, на рис. 12.28 показаний 4-мірний

Рис. 12.28. 4-мірний куб

У багатопроцесорній системі, базованій на гіперкубічній мережі, процесори розмі­щуються у вершинах графа. Дуги графа представляють канали зв’язку між процесора­ми. Як видно з рисунку, кожен процесор в 4-мірному кубі з’єднаний з чотирма іншими процесорами. У п-мірному кубі кожний процесор має канали зв’язку з п іншими про­цесорами. Оскільки в гіперкубі є дуга між заданою парою вузлів лише якщо двійкове представлення їх адрес відрізняється одним бітом, ця властивість забезпечує простий механізм маршрутизації повідомлень. Маршрут повідомлення, що відправляється з вуз­ла і та призначене для вузла ], може бути знайдений шляхом виконання над двійковим представленням адрес і та) операції виключного АБО (ХОІІ). Якщо результат виконання операції ХОІІ приводить до 1 в заданій бітовій позиції, то повідомлення має бути посла­ним по каналу зв’язку, який охоплює відповідний вимір. Наприклад, якщо повідомлен­ня послане від початкового (Б) вузла 0101 до вузла призначення (Б) 1011, то результатом операції ХОІІ буде 1110. Це означатиме, що повідомлення буде послано лише уздовж вимірів 2, 3, і 4 (рахуючи справа наліво) для того, щоб прибути до місця призначення. Порядок, в якому повідомлення перетинає три виміри, не має важливого значення. Як тільки повідомлення перетинає три виміри в будь-якому порядку, воно досягне місця призначення. Три можливих непересічних маршрути, які може пройти повідомлення у наведеному прикладі, показані виділеними лініями на рис. 12.28. Непересічні маршрути не мають будь-яких спільних каналів зв’язку.

У п-мірному кубі кожен вузол має порядок п. Порядок вузла визначений як число каналів зв’язку, що входять в вузол. Верхня межа кількості непересічних каналів в п- мірному кубі рівна п. Гіперкуб представляється як логарифмічна архітектура. Це тому, що максимальне число каналів зв’язку, які повідомленню доведеться перетнути, щоб до­сягти місця призначення, в п-мірному кубі, що містить N=2" вузлів, рівне ^.Д¹.

Одна з бажаних особливостей гіперкубічних мереж - рекурсивна природа 'їх побу­дови. п-мірний куб може бути побудований на основі двох підкубів, кожен з яких має порядок п-1, шляхом з’єднання вузлів подібних адрес в обох підкубах. Так 4-мірний куб, показаний на рис. 12.28, побудований на основі двох підкубів, порядок кожного з яких рівний трьом. Потрібно відзначити, що побудова 4-мірного куба на основі двох 3-мірних кубів вимагає збільшення порядку кожного вузла.

Система ІР5С фірми Меі є прикладом базованої на гіперкубічній комунікаційній ме­режі комерційної багатопроцесорної комп’ютерної системи.

Шинні динамічні комунікаційні мережі багатопроцесорних систем

Як ми вже вказували, динамічні комунікаційні мережі багатопроцесорних систем можуть бути одно- та багатошинними. Нарис. 12.29 наведено приклад використання од- ношинної комунікаційної мережі, яка є найпростішим варіантом з можливих з’єднань. В загальному вигляді така система включає N процесорів Р, кожен з яких має свою локаль­ну пам’ять, які з’єднані спільною шиною. Всі процесори через шину взаємодіють з спіль­ною пам’яттю. Типовий розмір таких систем - від одного до 50 процесорів. Він визнача­ється потрібного пропускною здатністю шини, яка приходиться на один процесор. Тому описана архітектура, при простоті розширення, обмежена пропускною здатністю шини, по якій одночасно може проводити обмін інформацією лише один процесор. Складність цієї мережі може бути оцінена наступним чином: апаратна асимптотична складність, ви­ражена кількістю магістралей, є 0(1), часова асимптотична складність, яка вимірюється кількістю затримок, є 0(ТЧ^т), де N - кількість процесорів.

Рис. 12.29. Однотипна багатопроцесорна система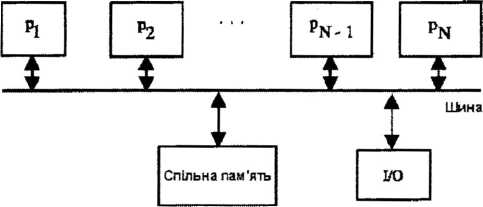

В табл. 12.1 наведено характеристики деяких комерційних одношинних багатопро­цесорних комп’ютерних систем.

Таблиця 12.1

Назва системи	Максимальна кількість процесорів	Тип процесора	Частота	Ємність пам'яті	Пропускна здатність шини
HP ШЮ K.640	4	РА-8900	180 MHz	4,0% MB	960 MB/S
IBM RS/6000 R40	8	PowerPC 604	і 12 МИ/.	2,048 MB	1.800 MB/s
Sim Enterprise (»000	30	UltraSPARC ]	і 67 MHz	30,720 MB	2.600 MB/s

Використання багатьох шин для з’єднання процесорів та блоків пам’яті є природнім розширенням одношинних систем. В цьому випадку можливі кілька варіантів схем з’єд­нань. Серед них можна відзначити наступні:

• багатошинна комунікаційна мережа з повним з’єднанням блоків пам’яті (multiple bus with full bus-memory connection),

• багатошинна комунікаційна мережа з одним з’єднанням блоків пам’яті (multiple bus with single bus memory connection),

• багатошинна комунікаційна мережа з частковим з’єднанням блоків пам’яті (multi­ple bus with partial bus-memory connecticyi),

• багатошинна комунікаційна мережа з базованим на класах з’єднанням блоків пам’яті (multiple bus with class-based memory connection)

• .

• В першому варіанті з’єднання, наведеному на рис. 12.30, всі блоки пам’яті під’єднані до всіх шин. Тут, як і на наступних рисунках, прийнято, що кількість процесорів N ~ 6, кількість модулів пам’яті М = 4, кількість шин В = 4.

• ‘

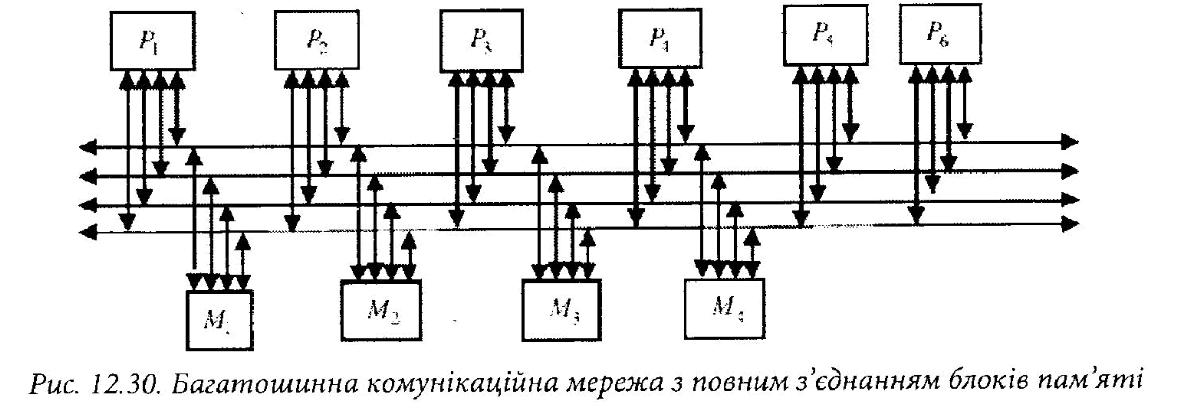
Цей варіант з’єднання є досить складним та дорогим, оскільки вимагає великої кіль­кості шин, реалізація яких вимагає значних апаратних ресурсів.

В другому варіанті (рис. 12.31) кожний модуль пам’яті під’єднаний до деякої однієї шини.

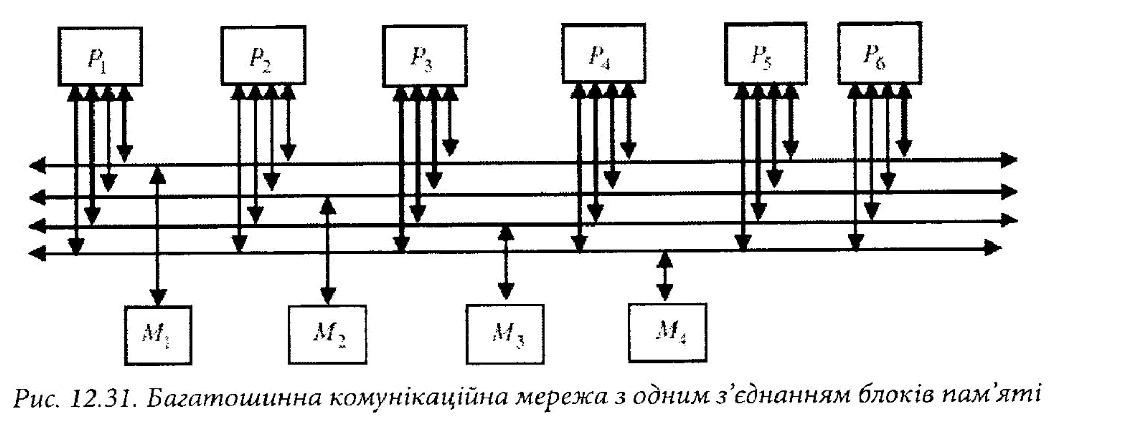
Тут структура комунікаційної мережі спрощується, однак можливі конфлікти досту­пу до блоків пам’яті.

В третьому варіанті (рис. 12.32) кожен модуль пам’яті під’єднаний не до всіх, як в першому варіанті, а до деякої групи шин (в даному випадку до двох шин).

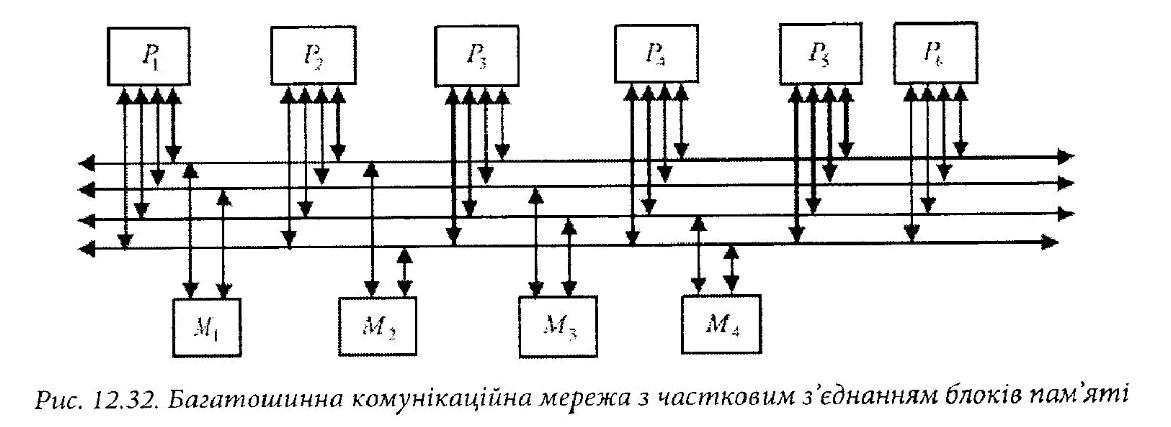
Тут клас - це довільно вибрана множина модулів пам’яті. Такий підхід також до­зволяє зменшити кількість конфліктів шляхом врахування особливостей виконуваних задач (інтенсивності обміну процесорів з пам’яттю). Можна характеризувати цей тип мережі використовуючи кількість необхідних зв’язків і навантаження на кожну шину, як показано в табл. 12.2, де наведені характеристики розглянутих багатошинних з’єднань. У цій таблиці к представляє число класів; g представляє число шин на групу, і М] пред­ставляє число модулів пам’яті в класі ].

В четвертому варіанті (рис. 12.33) модулі пам’яті згруповані в класи, які під’єднані до свого набору шин.

Клас 1 Клас? КласЗ

Рис. 12.33. Багатошинна комунікаційна мережа з базованим на класах з’єднанням блоків пам’яті

Таблиця 12.2

Тип з'єднання	Кількість з'єднань	Нзвзнтаженни на шину і
3 повним з’єднанням	В(М+М)	м+м і
3 одним з'єднанням	ійУ + М
3 частковим з'єднанням	ЖЛ'+МДе)	N 4- М /£ 1
3 базованим на класах з'єднанням	и + м,<л-в-	к) N + Ц;=іиам,+*-В.І) М}. 1 < І < В

В цілому багатошинна багатопроцесорна організація має кілька бажаних особливос­тей, таких як висока надійність і легкість нарощування. Коли кількість шин є меншою за кількість модулів пам’яті (або кількості процесорів), змагання за володіння шиною посилюється.

Важливим питанням в багатошинній багатопроцесорній організації є шинна синх­ронізація. Інформація може бути передана по шині синхронно або асинхронно. Час для будь-якої передачі по синхронній шині відомий наперед. При прийманні та відправленні інформації через ніину потрібно брати до уваги час передачі. Організація асинхронної шини, з другого боку, залежить від наявності даних і готовності пристрою ініціювати шинні операції.

В одношинній багатопроцесорній системі потрібен шинний арбітраж для вирішення шинного конфлікту, який має місце, коли більш ніж один процесор конкурує за оволо­діння шиною. В даному випадку процесори, які хочуть використовувати шину, подають запити до шинної арбітражної логіки. Арбітр вирішує, використовуючи схему пріорите­ту, якому процесору буде надано доступ до шини протягом певного часового інтервалу.