53. Пристрій керування на основі таблиць станів.

Абстрактні автомати

Метод таблиць станів передбачає розгляд пристрою керування як цифрового авто­мату, тобто логічного пристрою, який забезпечує формування сигналів керування за відповідним алгоритмом з врахуванням своїх внутрішніх станів.

Цифровий автомат можна подати у вигляді його математичної (абстрактної) і струк­турної моделей, які відповідно називаються абстрактним та структурним автоматами. Абстрактну модель використовують на першому етапі проектування, коли описують функціонування автомату, тобто правила переробки вхідної інформації у вихідну. На цьому етапі автомат подається у вигляді “чорної скриньки”. Розгляд абстрактної моде­лі цифрового автомату дозволяє проводити його попередню оптимізацію ще до етапу структурного синтезу. Структурну модель застосовують для побудови схеми цифрового автомату.

В подальшому будемо використовувати так званий скінчений абстрактний автомат, в якого множина внутрішніх станів і множина вхідних сигналів (а, отже, й множина ви­хідних сигналів) є скінченими множинами, повністю визначений (детермінований) аб­страктний автомат, в якого функція переходів 5 і функція виходів X визначені для всіх пар (x_nSj ), та ініціальний абстрактний автомат, в якого один із станів s₀ є S виділено як початковий стан, з якого автомат завжди починає роботу.

Отже, на абстрактному рівні функціонування цифровий автомат розглядається як перетворювач вхідних слів у вихідні слова, які складаються з букв вхідного і вихідного алфавіту. Внутрішні стани автомату - це інформація про минуле (передісторію) розви-, тку процесу керування в часі. Вона дозволяє використати час як явну вхідну змінну. По­трібно відзначити, що абстрактний автомат функціонує в дискретному часі, а переходи з одного стану в інший проводяться миттєво.

Залежно від способу генерування значень вихідних сигналів розрізняють три типи автоматів: Мілі, Мура, С-автомат.

Автомат Мілі описується наступною системою рівнянь:

Автомат Мілі можна представити у вигляді структурної схеми (рис. 8.4), вузли якої представляють відповідно функцію виходів X > функцію переходів 8 і пам’ять станів S, та з’єднані між собою відповідними зв’язками. Значення на його виході в момент часу t визначається значенням в даний момент на його вході та його станом, а також функцією виходів. Стан автомату Мілі в момент часу t+1 визначається значенням в даний момент на його вході та його станом, а також функцією переходів.

Автомат Мура описується наступною системою рівнянь:

y(t) = L(s(t))

s(/ + l) = 8 (x(t) s(0).

Автомат Мура також можна представити у вигляді структурної схеми (рис. 8.5), вуз­ли якої представляють відповідно функцію виходів А,, функцію переходів 8 і пам’ять станів S, та з’єднані між собою відповідними зв’язками.

Рис. 8.5. Автомат Мура

Значення на його виході в момент часу t визначається його станом в даний момент, а також функцією виходів. Стан автомату Мура в момент часу t+І визначається значен­ням в даний момент на його вході та його станом, а також функцією переходів. С-автомат описується наступною системою рівнянь: y_l(t)=\(x(t) s(t)) y₂(t)=\₂(s(t)) s(t + l) = b(x(t) s(t))

С-автомат можна представити у вигляді структурної схеми (рис. 8.6), вузли якої пред­ставляють відповідно функції виходів X 1 та X 2, функцію переходів 8 і пам’ять станів S, та з’єднані між собою відповідними зв’язками. Цей автомат має два виходи. Значення на першому його виході в момент часу t визначається значенням в даний момент на його вході та його станом, а також першою функцією виходів. Значення на його другому ви­ході в момент часу t визначається його станом в даний момент, а також другою функцією виходів. Стан автомату в момент часу t+І визначається значенням в даний момент на його вході та його станом, а також функцією переходів.

Рис. 8.6. С-автомат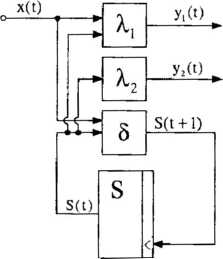

Фактично С-автомат є комбінацією автоматів Мілі та Мура.

Мови опису функціонування автоматів

Для того, щоб задати абстрактний автомат, потрібно задати всі п’ять об’єктів

{л'.яг.бЛ}.

Множини X, Б, У задаються як звичайні множини в математиці, наприклад, простим перелічуванням всіх її елементів, тому їх задання на практиці не викликає ніяких труд­нощів.

Найбільш трудомістким є задання функцій 5 Д , які власне і визначають алгоритм функціонування автомату. Для опису алгоритму функціонування автомату, тобто для задання 8 Д, існують різні засоби, які часто називають мовами. Існують стандартні та початкові мови. Стандартні мови задають автомат одним із трьох способів: матрично (таблично), графічно, аналітично. До початкових мов відносять первісні таблиці вклю­чень, логічні схеми алгоритмів і граф-схеми алгоритмів. Стандартні мови частіше засто­совуються для задання автоматів загального виду, в той же час початкові мови знайшли широке застосування для часткових автоматів.

Мова матриць (таблиць) передбачає наявність двох таблиць: таблиці переходів і та­блиці виходів, або однієї таблиці з’єднань.

Таблиця переходів задає відображення X х 5 —> 8, тобто задає функцію переходів

Приклад. Нехай на автомат поступають вхідні сигнали, які мають три букви, та нехай він має чотири стани: X = {х_р х₂, 5 = 5,, 5₃, 5₄}. В табл. 8.1 описано повністю визна­чений автомат для даного прикладу.

Таблиця 8.1

\Х(0 3(0\	Х1	Х2	ХЗ
Б1	Б1	Б2	Б1
Б2	БЗ	Б4	Б2
БЗ	БЗ	Б1	Б4
Б4	БЗ	Б1	52

З першого рядка табл. 8.1 видно, що перебуваючи в стані 51 при поступленні вхідно­го сигналу XI автомат не змінює свого стану, так само як і при поступленні вхідного сиг­налу ХЗ, а при поступленні вхідного сигналу Х2 він перейде в стан 52. Подібним чином можна провести аналіз інших рядків таблиці.

Якщо автомат частковий, то для пар (х„ $,), для яких стан не визначений, в клітинці таблиці ставиться прочерк. Як видно, вигляд таблиці переходів не залежить від того, який тип автомату використовується: Мілі, Мура чи С-автомат.

Таблиці виходів цих автоматів відрізняються.

У клітинці таблиці виходів автомату Мілі ставиться вихідний сигнал у_к, який фор­мує автомат Мілі, що знаходиться в стані 5_;- і на вході якого діє сигнал х.. Приклад по­вністю визначеного автомату Мілі з вхідним алфавітом X = {х,, х₂, х₃}, алфавітом станів; 5 = {5_Р 5₂, 5₃,5₄/ та вихідним алфавітом У = {у,, у₂, у₃} наведено в табл. 8.2.

Таблиця 8.2

\Х(1)	Х1	Х2	ХЗ
Є1	У1	У1	У2
32	УЗ	УЗ	УЗ
БЗ	У2	У1	УЗ
Б4	У2	У1	УЗ

З першого рядка табл. 8.2 видно, що перебуваючи в стані Б1 при поступленні вхідного сигналу XI на виході автомату буде сформовано сигнал У1, так само, як і при поступлен­ні вхідного сигналу Х2, а при поступленні вхідного сигналу ХЗ на виході автомату буде сформовано сигнал У2. Подібним чином можна провести аналіз інших рядків таблиці.

В таблиці виходів повністю визначеного автомату Мура кожному стану автомату призначається відповідний вихідний сигналу. Приклад повністю визначеного автомату Мура з алфавітом станів 5 = {$,, $₂, 5₃, та вихідним алфавітом У = {у,, у₂, наведено в табл. 8.3.

Таблиця 8.3

3(1)	У(і)
	У1
32	У1
гз	У2
34	УЗ

З табл. 8.3 видно, що стану Б1 та Б2 автомату відповідає вихідний сигнал УІ, стану БЗ відповідає вихідний сигнал У2, а стану Б4 відповідає вихідний сигнал УЗ.

С-автомат буде задаватися двома таблицями виходів, перша з яких відповідає табли­ці виходів автомату Мілі, а друга - таблиці автомату Мура.

На практиці таблиці переходів і таблиці виходів часто суміщаються в одну суміщену таблицю. Табл. 8.4 є суміщеною таблицею автомату Мілі для вищенаведеного прикладу.

\Х(() 3(1Г\	Х1	Х2	ХЗ
в1	31/У1	S2/У^	Б1/У2
Б2	Б З/УЗ	34/УЗ	Б2/У3
вз	Б3/У2	ві/п	Б4/У3
в4	53/У2	гі/уі	Б2/У3

Таблиця 8.4

З першого рядка табл. 8.4 видно, що перебуваючи в стані Б1 при поступленні вхідно­го сигналу XI автомат залишиться в тому ж стані, а на виході автомату буде сформовано сигнал У1, при поступленні вхідного сигналу Х2 автомат перейде в стан Б2, а на виході автомату буде сформовано сигнал Уі, при поступленні вхідного сигналу ХЗ автомат за­лишиться в тому ж стані, а на виході автомату буде сформовано сигнал У2. Подібним чином можна провести аналіз інших рядків таблиці.

Як вже зазначилось вище, можна задати керуючий автомат за допомогою єдиної та­блиці з’єднань. Таблиця з’єднань абстрактного автомату є квадратною і містить стільки стовпців та рядків, скільки різних станів має даний автомат. В клітинці ставиться вхід­ний сигнал, під дією якого відбувається перехід автомату зі стану в стан. Якщо матри­цею з’єднань задається автомат Мілі, то разом з вхідним сигналом вказується вихідний сигнал, який автомат Мілі видає, виконуючи перехід (табл. 8,5).

Таблиця 8.5

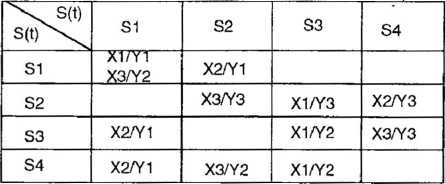
З першого рядка табл. 8.5 видно, що автомат залишається в тому ж стані Б1 при посту­пленні вхідних сигналів XI та ХЗ, і при цьому на його виході будуть відповідно сигнали У1, та У2, та переходить в стан Б2 при поступленні вхідного сигналу Х2, і при цьому на його виході буде сигнал У1. Подібним чином можна провести аналіз інших рядків таблиці.

Для автомату Мура в матриці з’єднань вихідні сигнали ставляться біля станів авто­мату, які ідентифікують рядки матриці.

Мова графіки передбачає застосування для задання абстрактного автомату орієнтова­ного графа. Стан автомату зображається вершинами графа, а переходи між станами - ду­гами між відповідними вершинами. При цьому конкретній дузі графа приписується буква х₁ вхідного алфавіту автомату, яка вказує на перехід при поступленні цього сигналу.

Якщо граф зображає автомат Мілі (рис. 8.7), то вихідні сигнали автомату ставляться на дугах графа (згідно з таблицею виходів) разом з буквою вхідного сигналу. Тут в якості прикладу взято автомат Мілі, описаний в табл. 8.4. Якщо графом зображається автомат Мура (рис. 8.8), то вихідні сигнали автомату ставляться біля вершини графа відповідно до таблиці виходів автомату (табл. 8.3).

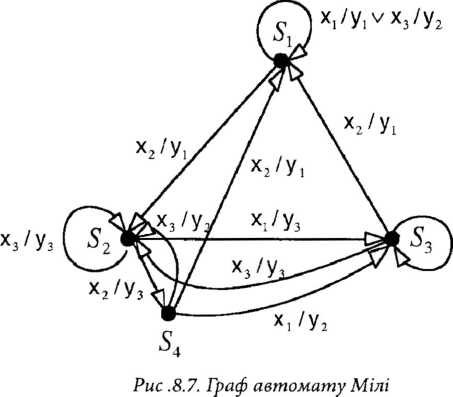
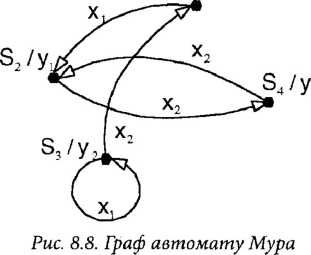
Мова аналітичних виразів передбачає задания автомату шляхом запису для кожного стану автомату відображення , яке містить набори з трьох об’єктів у_к, причому тільки таких, які вказують на наявність переходу автомату зі стану 5^. в стан при дії вхідного сигналу х_і і видачі при цьому вихідного сигналу у_к.

Структурний синтез цифрових автоматів

Процес одержання структурної схеми, яка відображає склад логічних елементів та їхні зв’язки, називають структурним синтезом. В загальному випадку задача структур­ного синтезу зводиться до композиції деяких простих автоматів, тобто до пошуку спо­собу з’єднань цих автоматів між собою. Як правило, ефективно розв’язується задача структурного синтезу тільки для певного набору простих автоматів певного виду - еле­ментарних автоматів, які складаються з елементів пам’яті, що мають більше одного стій­кого стану (елементарних автоматів з пам’яттю) та комбінаційних схем (елементарних автоматів без пам’яті).

Метод синтезу, в основу якого покладені елементарні автомати, отримав назву ка­нонічного методу структурного синтезу автоматів. Загальна структура елементарного автомату, що складається з пам’яті та комбінаційної схеми, представлена на рис. 8.9.

Елементарний автомат має кх входів р 1 р 2... р кх, ку виходів со,со₂ та кБ виходів пам’яті станів а_аа₂...а_к . Сигнали керування пам’яттю м_],и₂,...и_к описуються за допо­могою булевих функцій, які називаються функціями збудження. Таким чином, для побу­дови структурного автомату потрібно мати елементи пам’яті і набір логічних елементів, які утворюють функціонально повну систему для побудови комбінаційної схеми.

Канонічний метод структурного синтезу розділяють на наступні етапи:

• кодування,

• вибір типу та структури абстрактного автомату,

• вибір елементів пам’яті,

• побудова рівнянь булевих функцій збудження і виходів автомату,

• побудова структурної схеми автомату.

Розглянемо кожен з етапів.

Кодування. Нагадаємо, що абстрактний автомат задається в вигляді А = (а^г,5',У,8,Х}. При переході на структурний рівень множини сигналів X та У, а також сигнали Б потріб­но зобразити у вигляді двійкового вектору.

Нехай 5 = {$_р $₂, $₄, $₉ 5^, тоді к₅ = ] /о&М, [ = ] log₂6 / = 3. Тобто для нумерації кожно­го стану потрібно 3 розряди, тоді s = {000,001,010,011,100,101}. Фізично в структурному авто­маті буде три стани, кожен з яких може прийняти тільки два значення 0 або 1. Сукупність значень цих трьох станів буде відповідати одному із станів абстрактного автомату.

Приклад: автомат описується суміщеною таблицею переходів та виходів (табл. 8.6).

\Х(І)	Х1	Х2
Э1	Б2/У1	Э1/У3
Б2	эз/уг	Б1/У4
ЭЗ	Є3/У1	Б2/У2

Таблиця 8.6

Тобто він має три стани М* = п = 3, два вхідних сигнали М_х = ш = 2 та чотири вихідних сигнали Му = 1 = 4. Вони відповідно можуть бути закодовані наступною кількістю роз- І рядів: К₅ = 2, К_х = 1 та К_у = 2.

Результати кодування вхідних сигналів наведено в табл. 8.7, станів - в табл. 8.8, та : вихідних сигналів - в табл. 8.9

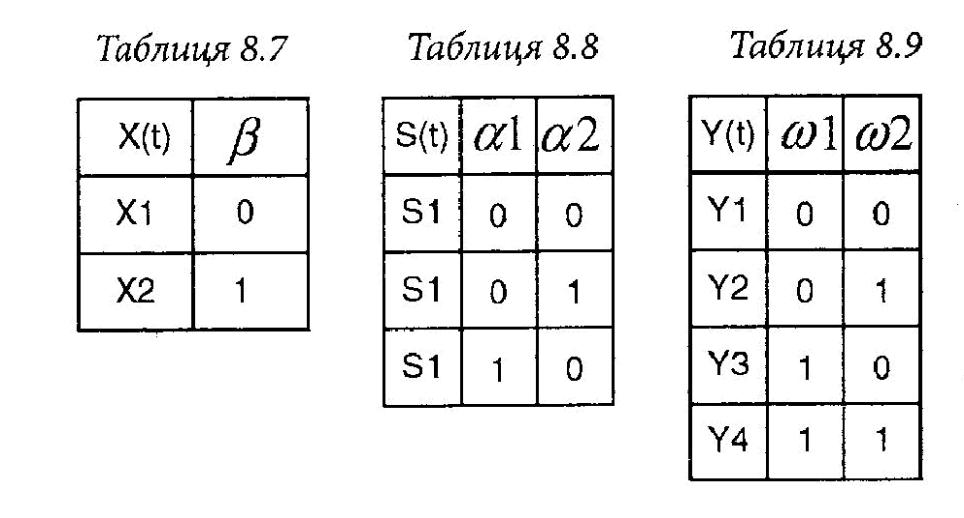
Тоді суміщена таблиця переходів та виходів (табл. 8.6) з закодованими входами, ста­нами та виходами, буде мати вигляд табл. 8.10.

Побудова абстрактного автомату

Структурна схема цифрового автомату Мілі для розглядуваного прикладу має ви­гляд, показаний на рис. 8.10.

Рис. 8.10. Структурна схема цифрового автомату для розглядуваного прикладу Вибір елементів пам’яті.

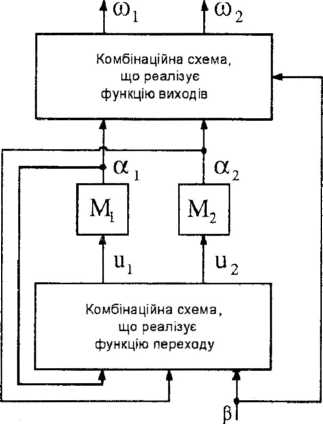
В якості елементів пам’яті структурного автомату можуть бути використані всі відо­мі типи тригерів, зокрема Б-тригери, КБ-тригери, Т-тригери, ДС-тригери.

Якщо в якості елементів пам’яті вибираються тригери, які мають вхід синхронізації, то структурний автомат буде синхронним, а якщо вибираються асинхронні тригери, то автомат буде асинхронним.

Побудова рівнянь булевих функцій збудження і виходів автомату.

Провівши кодування та вибравши систему логічних елементів, можна однозначно визначити структуру комбінаційних схем автомату. Рівняння булевих функцій будують­ся на основі таблиці істинності функції збудження, яка в свою чергу будується на основі структурної таблиці переходів і таблиці переходів елемента пам’яті. Для наведеної вище таблиці маємо