Випадкові величини та їх розподіли

Випадкові величини. Функція розподілу випадкової величини

Розглядаючи випадкові експерименти, дотепер нас цікавили їх можливі наслідки. Але із можливими наслідками експерименту можна пов’язати певну величину, яка в залежності від наслідку експерименту приймає деякі числові значення. Наприклад, при киданні грального кубика нас цікавить число очок, які є на грані. При контролі якості продукції нас може цікавити число бракованих виробів серед випадково взятих n виробів. При проведенні пострілів по мішені кожній точці попадання ставимо у відповідність величину, яка дорівнює віддалі від цієї точки до центра мішені. Тобто, з кожним експериментом ми пов’язуємо величину, яка в залежності від випадку приймає деякі числові значення. Таку величину називають випадковою. Якщо в експерименті спостерігається певна випадкова величина , то при виборі будь-якого із повинно бути задане значення цієї величини . Отже, випадкову величину можна розглядати, як функцію визначену на просторі елементарних подій . Ця функція повинна задовольняти деяким додатковим умовам. Для цього ми спочатку визначимо поняття борелєвої алгебри.

Означення 1. Нехай задано ймовірнісний простір . Випадковою величиною називається будь-яка дійсна функція , що відображає простір елементарних подій в множину дійсних чисел R, для якої прообраз будь-якої борелєвої множини є множина із алгебри : .

Сформулюємо деякі висновки, що випливають із властивостей вимірних функцій. Звідси, зокрема, одержуємо, що множини , , , , , є випадковими подіями.

Якщо випадкові величини і визначені на одному і тому ж ймовірнісному просторі, то , , є також випадковими подіями.

Ми будемо також розглядати і події, що пов’язані із нескінченними послідовностями випадкових величин. Нехай - послідовність випадкових величин, що задані на ймовірнісному просторі , і - випадкова величина на . Тоді існує} , .

Означення 2. Ймовірність називається розподілом випадкової величини .

Означення 3. Нехай . Тоді функція називається функцією розподілу випадкової величини . Тобто, функція, яка для кожного дійсного x визначається рівністю

,

називається функцією розподілу випадкової величини .

Функція розподілу випадкової величини повністю визначає її розподіл.

Там, де це не викличе непорозуміння, замість писатимемо . Отже,

.

Як приклад, розглянемо рівномірний розподіл на відрізку [a,b]. На рідрізок [a,b] випадково кидається точка, причому вважаємо, що всі положення точки рівноможливі (ймовірність попадання точки на деяку частину відрізка пропорційна мірі цієї частини). Простір елементарних подій , є -алгебра борелєвих підмножин даного відрізка, P(.) – така міра, що , якщо . Визначимо випадкову величину , якщо , тобто - координата вибраної точки. Тоді для довільного x

Тому і – випадкова величина, а її функція розподілу має вигляд:

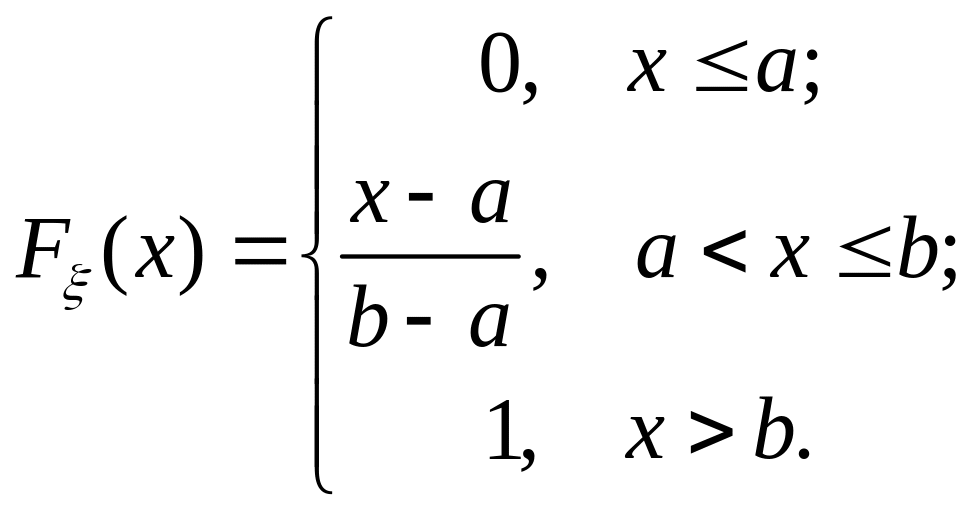
Відзначимо, що для різних випадкових величин їх функції розподілу можуть співпадати. Наприклад, нехай , , , , – випадкова величина, що визначена на : Тоді

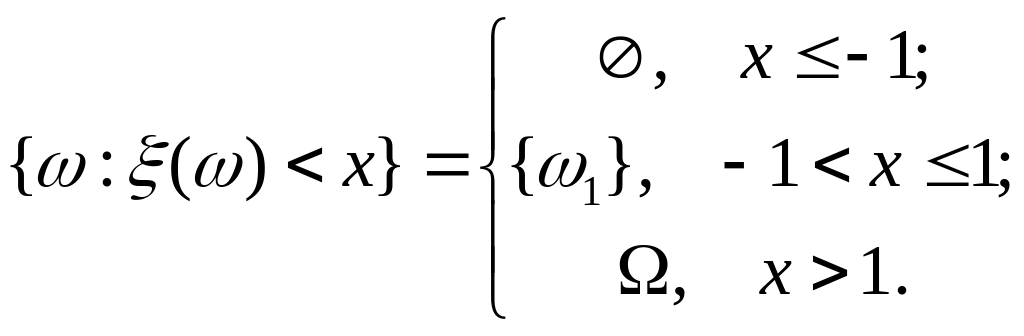
Із визначення функції розподілу одержуємо:

Розглянемо нову випадкову величину Тоді, очевидно,

Якщо , то . Отже, різні випадкові величини можуть мати однакові функції розподілу.

Властивості функції розподілу

1. , бо , а ймовірність міститься в межах від 0 до 1.

2. - неспадна: для довільних .

Наслідок. .

3. Функція розподілу неперервна зліва, тобто, .

4. , .

Дискретні випадкові величини

Означення. Випадкова величина називається дискретною, якщо множина її значень скінченна або зліченна.

Можливі значання дискретної випадкової величини характеризують її ще не повністю, а для повної ймовірнісної характеристики випадкової величини необхідно знати і ймовірності, з якими ці значення приймаються.

Якщо – дискретна випадкова величина, що приймає значення , то для кожного n визначена ймовірність

. (1)

Набір ймовірностей (1) називають розподілом випадкової величини .

Відповідність між можливими значеннями випадкової величини та ймовірностями, з якими ці значення приймаються, називається законом розподілу (рядом розподілу) дискретної випадкової величини.

Оскільки події утворюють повну групу, то і

.

Закон розподілу дискретної випадкової величини зручно подавати у вигляді таблиці:

Значення			…		…
Ймовірності			…		…

За законом розподілу дискретної випадкової величини можна знайти її функцію розподілу. Якщо , то подія , тому . Якщо , то . Тому . Отже,

. (2)

Функція розподілу дискретної випадкової величини має скінченні розриви у кожній точці і величина розриву, за властивістю 5, дорівнює . Між сусідніми точками розриву функція розподілу є сталою.

Розглянемо приклади важливих дискретних розподілів.

Біномний розподіл. Нехай проводиться незалежних випробувань, в кожному із яких ймовірність настання події A дорівнює p. Біномним розподілом називається розподіл випадкової величини , яка дорівнює числу настання події в випробуваннях Бернуллі. Можливими значеннями випадкової величини є числа k = 1, 2, … , n, а відповідні ймовірності знаходяться за формулою Бернуллі

.

Як ми уже відзначали, .

Розподіл Пуассона. Випадкова величина має розподіл Пуассона із параметром >0, якщо вона приймає значення 0, 1, … , n, …, а відповідні ймовірності знаходяться за формулою:

.

Очевидно, .

Розподіл Пуассона відіграє важливу роль в теорії випадкових процесів, теорії масового обслуговування, теорії надійності. Розподіл Пуассона є граничним для біномного розподілу.

Геометричний розподіл. Випадкова величина має геометричний розподіл, якщо вона дорівнює числу експериментів до першої появи події в схемі Бернуллі (без експерименту, в якому подія настала).

Нехай , тоді множина може розглядатись як простір елементарних подій. Враховуючи незалежність подій, одержуємо: . Отже,

і

.

Нехай , тоді . Дійсно,

.

Наведена властивість геометричного розподілу називається властивістю відсутності післядії. Відзначимо, що серед всіх дискретних розподілів цю властивість має тільки геометричний розподіл.

Абсолютно неперервні розподіли. Щільність розподілу випадкової величини

Означення. Нехай випадкова величина має функцію розподілу . Якщо існує така інтегровна функція , що для всіх дійсних x виконується рівність

, (3)

то розподіл називається абсолютно неперервним, а називається щільністю розподілу випадкової величини.

, (5)

. (6)

Графік функції називається кривою розподілу

Наведемо приклади найбільш важливих неперервних розподілів.

Рівномірний розподіл на відрізку [a,b]. На відрізок [a,b] випадково кидається точка, причому вважаємо, що всі положення точки рівноможливі. Визначимо випадкову величину , якщо , тобто – координата вибраної точки. В прикладі 1 ми показали, що функція розподілу випадкової величини має вигляд:

Тому щільність розподілу випадкової величини

Значення випадкової величини, що має рівномірний розподіл на відрізку , одержане внаслідок експерименту, називають випадковим числом. На основі випадкових чисел із рівномірного розподілу можна моделювати випадкові величини із будь-яким наперед заданим розподілом.

Нормальний розподіл. Випадкова величина має нормальний розподіл із параметрами і , якщо її щільність розподілу

.

Позначаємо: ~ . Якщо , а , то – функція Гауса, тоді розподіл називається стандартним.

Функція розподілу має вигляд:

.

Використовуючи інтеграл Пуассона, одержимо:

.

Нехай – функція Лапласа, – функція розподілу стандартного нормального закону, тоді

.

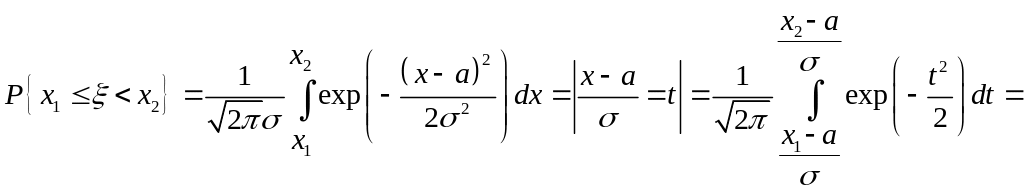
Тобто,

.

Як частинний випадок,

.

Якщо у попередній формулі покласти , то . Тому нормально розподілена випадкова величина з ймовірністю досить близькою до одиниці приймає значення, що відрізняються від параметра a не більше, ніж на .

Якщо випадкова величина ~ , то ~ , тобто буде мати стандартний нормальний розподіл:

.

Показниковий розподіл. Випадкова величина має показниковий розподіл із параметром , якщо

Очевидно,

.

Знайдемо функцію розподілу. Нехай , тоді . Якщо ж , то . Отже,

Відзначимо, що показниковий розподіл має властивість відсутності післядії: при

.

Тобто, при

.

Серед всіх неперервних розподілів цю властивість має тільки показниковий розподіл.

Гамма-розподіл. Розглянемо гамма-функцію . Зробимо в інтегралі заміну , де . Тоді

і

.

Тому для функції

виконуються умови (4) і (5). Отже, вона є щільністю розподілу деякої випадкової величини. Розподіл із такою щільністю називається гамма-розподілом із параметрами .

Багатовимірні випадкові величини

Випадкові вектори, їх розподіли. Нехай на ймовірнісному просторі задані випадкові величини . Вектор - називається -вимірним випадковим вектором або -вимірною випадковою величиною.

.

Ймовірність називають розподілом випадкового вектора . У частинному випадку, якщо , одержимо функцію, яку називають функцією розподілу випадкового вектора :

.

Подія розглядається як сумісне настання подій ,…, .

Очевидно,

.

,

.

Із останньої властивості випливає, що за функцією розподілу вектора можна знайти функцію розподілу вектора для довільного k=1,…,m, зокрема, можна знайти функцію розподілу кожної компоненти вектора.

Відзначимо також, що функція розподілу по кожній із змінних неспадна і неперервна зліва.

Розглянемо двовимірний випадковий вектор . Тоді для функції розподілу будуть справедливі рівності:

,

, ,

.

Якщо існує функція така, що

,

то функцію називають щільністю розподілу випадкового вектора , а розподіл випадкового вектора називають абсолютно неперервним.

Із даного означення випливає:

1) ;

2) якщо – точка неперервності , то ;

3) ;

4) для довільної борелєвої множини

.

Знаючи щільність розподілу випадкового вектора, можна знайти щільності розподілу його компонент. Розглянемо, як частинний випадок, двовимірну випадкову величину зі щільністю . Тоді

,

звідки

,

а

.

Випадковий вектор називається дискретним, якщо множина його значень скінченна або зліченна. Розглянемо для спрощення двовимірну випадкову величину . Нехай , , , , тоді кожній парі можна поставити у відповідність ймовірність . Тут . Таку відповідність називають законом розподілу. Його можна подати у вигляді такої таблиці:

		.....
		.....
…	…	.....	…..	…..
		.....
		.....

Якщо , то утворюють повну групу і , тому 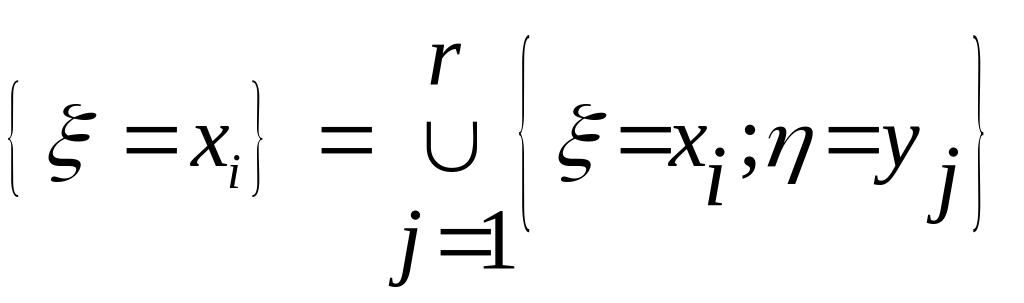. Отже, за аксіомою адитивності . Так само . При цьому, .

Деякі розподіли функцій від нормально розподілених випадкових величин. Нехай випадкові величини – незалежні, . Тоді випадкова величина має розподіл Пірсона (або розподіл ) із ступенями вільності.

Нехай – незалежні нормально розподілені з параметрами випадкові величини. Тоді величина має розподіл Стьюдента (або -розподіл) із ступенями вільності.

Нехай , – незалежні нормально розподілені з параметрами випадкові величини, . Тоді величина має розподіл Фішера із ступенями вільності.

Нормальний розподіл, розподіли Пірсона, Стьюдента, Фішера мають дуже широке використання у математичній статистиці.