4.3. Число зубьев передачи
Принимаем Z3 = 22
тогда Z4 = Z3uозп= 22∙2,24 = 49,3
Принимаем Z4 = 49
4.4.Анализ расчета на прочность по изгибу зуба
Определяем коэффициенты формы колес. Проектируемая открытая
цилиндрическая передача прямозубая, поэтому Zэкв = Z
для Z3 =22→ YF3 = 4,0
для Z4 =49→ YF4 = 3,66
Сравниваем отношения
[σ]F3/ YF3 = 189,9/4,0 = 47,47 МПа
[σ]F4/ YF4 = 166,2/3,66 = 45,4 МПа
Для колеса данное отношение меньше [σ]F3/ YF3 >[σ]F4 /YF4, поэтому
дальнейший расчет производим по колесу Z4.
4.5. Модуль передачи
m = Km(MрвKFβYF4/Z42ψbd[σ]F4)1/3
где Km = 1,4 для прямозубой передачи:
KFβ =1,04 - коэффициент неравномерности распределения нагрузки
по ширине зубчатого венца при несимметричной установке колеса относительно опор;
ψbd - коэффициент ширины зубчатого венца;
ψbd = 0,5ψbа(uозп+1)
где ψbа – стандартный коэффициент зубчатого венца по ГОСТ 2185-66
принимаем ψbа = 0,315, тогда
ψbd = 0,5∙0,315∙(2,2+ 1) = 0,504
m = 1,4(1849∙103∙1,04∙3,66/(492∙0,504∙166,2))1/3 = 4,59 мм
Учитывая повышенный износ зубьев открытой передачи, увеличиваем
модуль в два раза и принимаем по ГОСТ 9563-60
m = 8 мм
Проверим возможность крепления шестерни , рассчитанной по модулю m=5 на первой ступени тихоходного вала.
Диаметр под шестерней Z3 по стандарту dвых =55 мм
На участке под шестерню имеется шпоночный паз для закрепления на нём шестерни открытой передачи. Имеется зависимость между размерами шестерни и диаметром участка под эту шестерню, которая выражается следующим неравенством:
[df3/2-(d(z)/2+t2)]>2,5m,где
df3- диаметр впадин зубьев шестерни
t2- глубина паза втулки под шпоночное соединение,t2=3,3 мм [3]с.302
df3 = d3 – 2,5m = mz3 -2,5m=8∙22– 2,5·8=156 мм
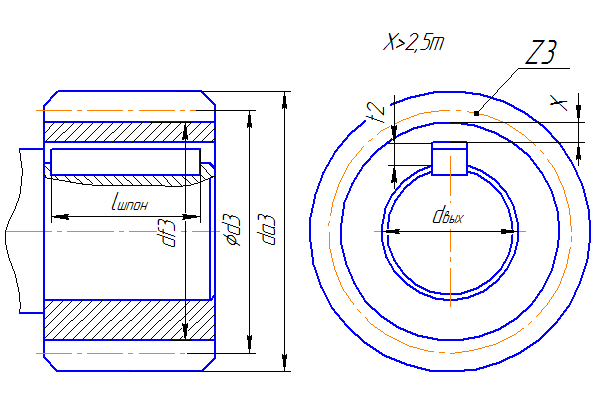
С учётом ранее рассчитанного значения модуля m=6мм:
[156/2-(55/2+4,3)]=46,2>2,5∙8=20 мм
Неравенство верно, значит при заданных параметрах открытая передача будет работать в нормальных условиях.
4.6. Основные размеры зубчатой пары
делительные диаметры
d3 = mz3 =8,0·22 = 176 мм
d4 = mz4 =5,0∙49 = 392 мм
диаметры выступов
da3 = d3+2m = 176+2·8= 192 мм
da4 = d4+2m =384+2·8= 408 мм
диаметры впадин
df3 = d3 – 2,5m = 176– 2,5·8=156 мм
df4 = d4– 2,5m =392– 2,5·8 =372 мм
межосевое расстояние
а = 0,5m(Z3+Z4) = 0,5∙8,0∙(22+49) =284 мм
ширина колеса
b4 = baaw = 0,315·284= 89,5 мм
Принимаем b4=90,0 мм
Ширину шестерни b5 рекомендуют проектировать на (2÷5)мм больше ширины колеса, так как возможна осевая ″игра″ передачи, неточность сборки.
Примем b3=95 мм
4.7. Проверочный расчет передачи по напряжению изгиба
σF4 = 2000YF4ТрвKFαKFβ/(b4md4)
где KFα – коэффициент неравномерности распределения нагрузки между зубьями, зависящий от степени точности изготовления зубчатых колес. При 8-ой степени точности KFα = 0,9
σF4 = 2000∙3,66∙1883∙0,9∙1,0/(90∙8,0∙392) = 46,2 МПа
Так как расчетные напряжения σF4 < [σ]F4 =166,2 МПа, то можно утверждать, что данная передача выдержит передаваемую нагрузку и будет стабильно работать в нормальных условиях.