33. Дискретні та інтервальні ряди розподілу.

Статистичний ряд розподілу - це впорядковані статистичні сукупності (табл. 17). Найпростішим видом статистичного ряду розподілу є ранжированний ряд, тобто ряд чисел, що знаходиться в порядку зростання чи спадання варіюючої ознаки.

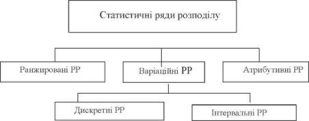
варіаційний ряд розподілу - це такий ряд, у якому варіанти розташовані в порядку зростання або спадання, вказані їх частоти або частості. Варіаційні ряди бувають дискретні (переривні) і інтервальні (непереривні).

Дискретні варіаційні ряди - це такі ряди розподілу, в яких варіанта як величина кількісної ознаки може приймати тільки певне значення. Варіанти різняться між собою на одну чи кілька одиниць.

Так, кількість вироблених деталей за зміну конкретним робітником може виражатися тільки одним певним числом . 

Інтервальні (непереривні) варіаційні ряди - такі ряди розподілу, в яких значення варіанти дано у вигляді інтервалів, тобто значення ознак можуть відрізнятися одне від одного на скільки завгодно малу величину. При побудові варіаційного ряду непереривної ознаки неможливо вказати кожне значення варіанти, тому сукупність розподіляється за інтервалами. Останні можуть бути рівні і нерівні. Для кожного з них вказуються частоти або частості (табл. 19).

В інтервальних рядах розподілу з нерівними інтервалами обчислюють такі математичні характеристики, як щільність розподілу і відносна щільність розподілу на даному інтервалі. Перша характеристика визначається відношенням частоти до величини того ж інтервалу, друга - відношенням частості до величини того ж інтервалу.

34. Концетрація та локалізація

Оцінка нерівномірності розподілу значень ознаки між окремими складовими сукупності грунтується на порівнянні часток двох розподілів – за кількістю елементів сукупності dj та за обсягом значень ознаки Dj . Відхилення часток свідчить про певну нерівномірність розподілу, яка вимірюється коефіцієнтами :

локалізації концентрації .

 

Коефіцієнт локалізації розраховується для кожної j-ї складової сукупності. За рівномірного розподілу всі значення Lj=1. У випадку концентрації значень ознаки в j-ій складовій Lj≥1, і навпаки.

Коефіцієнт концентрації є узагальнюючою характеристикою відхилення розподілу від рівномірного. Значення його коливаються у межах від 0 до 1. У рівномірному розподілі К=0. Чим помітніша концентрація, тим більше значення К відхиляється від 0.

Коефіцієнти концентрації та локалізації є ефективним засобом вимірювання диференціації сукупності за даними інтервальних рядів з нерівними інтервалами та за даними атрибутивних рядів. За аналогією з коефіцієнтом концентрації розраховують коефіцієнт подібності (схожості) структур двох об’єктів або одного об’єкта за двома ознаками: .

Якщо структури однакові, Р=1. Чим більші відхилення структур, тим менше значення коефіцієнта Р.

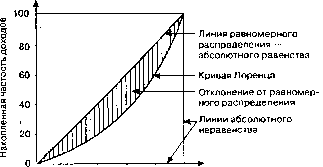
35. Крива Лоренца

Кривая Лоренца — это графическое изображение функции распределения, изобретена  как показатель неравенства в доходах населения. В таком представлении она есть изображение функции распределения, в котором кумулируются доли численности и доходов населения. В прямоугольной системе координат кривая Лоренца является выпуклой вниз и проходит под диагональю единичного квадрата, расположенного в I координатной четверти.

Каждая точка на кривой Лоренца соответствует утверждению вроде «20 самых бедных процентов населения получают всего 7 % дохода». В случае равного распределения каждая группа населения имеет доход, пропорциональный своей численности. Такой случай описывается кривой равенства (line of perfect equality), являющейся прямой, соединяющей начало координат и точку (1;1). В случае полного неравенства (когда лишь один член общества имеет доход) кривая (line of perfect inequality) сначала «прилипает» к оси абсцисс, а потом из точки (1;0) «взмывает» к точке (1;1). Кривая Лоренца заключена между кривыми равенства и неравенства.

Кривые Лоренца применяют для распределений не только доходов, но и имущества домохозяйств, долей рынка для фирм в отрасли, природных ресурсов по государствам. Встретить кривую Лоренца можно и за пределами экономической науки.