31. Структурні середнц.
Поряд з розглянутими вище середніми, для статистичної характеристики варіантних рядів обчислюють так звані структурні (порядкові) середні, до яких відносять моду і медіану. В розподілах, де всі варіанти зустрічаються однакове число раз, моди немає взагалі, або говорять, що всі варіанти однаково модальні. Якщо два варіанти мають однакові частоти, тоді буде дві моди, тобто розподіл буде бімодальним. Медіана - це варіант, який займає середнє положення в рангованому варіаційному ряді. Щоб знайти медіану в дискретному варіаційному ряді, потрібно спочатку розташувати всі варіанти в зростаючому або спадаючому порядку. Потім визначити номер медіани, який вкаже на її розташування в рангованому ряді, за формулою: п + 1 № Мє = , де Ме - медіана; п - число варіантів.
Середні показники динамічного ряду.
Середні рівні використовують насамперед для узагальнення коливних рядів. Наприклад, при аналізі динаміки сільськогосподарського виробництва оперують не річними, а більш сталими середньорічними показниками за певні періоди. Середні рівні необхідні також для забезпечення порівнянності чисельника і знаменника при побудові динамічних рядів похідних показників. Наприклад, виробництво продукції на одного працюючого. Обсяг продукції — інтервальний показник, а кількість працюючих — моментний. Щоб забезпечити порівнянність цих показників, слід обчислити середньорічну кількість працюючих.
Метод обчислення середнього рівня динамічного ряду залежить від статистичної структури показника. В інтервальному ряді абсолютних величин, рівні якого динамічно адитивні, використовується середня арифметична проста:
,
де n — число рівнів ряду.
У моментному ряді, за припущення про рівномірну зміну показника між датами, середня розраховується як півсума значень на початок і кінець періоду:
.
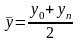Якщо в моментному ряді n > 2 і між суміжнимі датами однакові інтервали, розрахунок виконується за формулою середньої хронологічної:
.
Обґрунтування та розрахунок такої середньої наведено в підрозд. 4.4.
У моментних рядах з різними інтервалами між датами розраховується середня арифметична зважена:
,
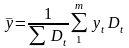де
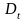— інтервал часу між датами, m
— кількість інтервалів.
Середній абсолютний приріст (абсолютна швидкість динаміки) обчислюється діленням загального приросту за весь період на довжину цього періоду у відповідних одиницях часу (рік, квартал, місяць тощо):
.
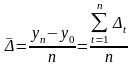Середні показники рядів динаміки.
1) Для моментного ряду:
• Середня арифметична зважена (даних достатньо) У̅=(∑уі*ti):∑ti де уі –рівень ряду на певний момент часу, а ti-тривалість ітого рівня
• Середньо модифікована(даних не достатньо, інтервали між наданими моментами часу не рівні) У̅=∑уi̅*ti:∑ti , де уі – середній рівень між 2-ма сусідніми моментами часу, а ti-тривалість часу між двома сусідніми моментами ряду
• Середньо хронологічна(даних недостатньо, інтервали Між наданими моментами часу рівні) У̅=((у1:2)+у2+…+уn-1+(yn:2)):n-1 Якщо є дані тільки на початок та кінець періоду, то у̅=(уп+yk):2
2) Для інтервального ряду
• Середня арифметична проста у̅=∑уі:n, де уі-рівень ітого періоду
• Середній абсолютний приріст1)∆̅=∑∆̅і:n для інтервального2)∆̅=(yi-y0):(n-1)для моментного
• Середній темп зростання Тзр̅=n-1√yi:y0=n-1√Тзр
• Середній темп приросту Тпр̅=Тзр̅(%)-100 (вимірюється в %)