
- •1.Асиметрія та ексцес
- •17. Коефіцієнти варіації та їх значення
- •18.Комбінаційне та аналітичне групування
- •19. Методи аналізу концентрації ознаки
- •22. Мода та медіана у варіаційних та інтервальних рядах.
- •20. Методи графічного аналізу рядів розподілу
- •21. Параматри рівняння парної лінійної регресії
- •24. Показники динаміки. Ланцюговий та базисний способи розрахунку
- •26. Показники приросту та зростання.
- •23. Оцінювання ваги факторів у рівняннях регресії
- •27. Середня та дисперсія
- •25.Показники концентрації та локалізації ознаки
- •28. Правило розкладання дисперсій. Кореляціцне відношення..
- •32. Характеристики центра розподілу величин.
- •31. Структурні середнц.
- •Середні показники динамічного ряду.
- •33. Дискретні та інтервальні ряди розподілу.
- •34. Концетрація та локалізація
- •35. Крива Лоренца
- •36. Гістограма, полігон, кумулята
- •37. Зважені та прості середні
- •38. Коефіцієнт кореляції
- •40.Нелінійні рівняння регресії
- •Статистика
22. Мода та медіана у варіаційних та інтервальних рядах.
Мода
– це значення варіанти, що найчастіше
повторюються в ряду розподілу. Дискретний
ряд – візуально за найбільшою частотою.
Для інтервальних рядів за формулою:![]()
Медіана
– це варіанта, яка ділить ранжирований
ряд на 2 рівні за обсягом частини.
Дискретний ряд:
1. Непарне число
варіант
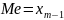 2.
Парне
число варіант
2.
Парне
число варіант
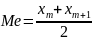
Інтервальні
ряди – визначає медіанний інтервал на
який припадає 50 відсотків і більше від
суми накопиченних частот. Визначається
за формулою:![]()
20. Методи графічного аналізу рядів розподілу
Ряди розподілу зручно вивчати за допомогою графічного методу. Статистичний графік — це креслення, на якому статистичні сукупності, що характеризуються певними показниками, описуються за допомогою умовних геометричних образів або знаків. Представлення даних таблиць у вигляді графіка справляє більш сильне враження, ніж цифри, дозволяє краще осмислити результати статистичного спостереження, правильно їх витлумачувати, значно полегшує розуміння статистичного матеріалу, робить його наочним і доступним.. Графічне зображення дозволяє здійснити контроль вірогідності статистичних показників, оскільки останні, будучи представлені на графіку, яскравіше виражають наявні неточності, пов'язані або з наявністю неточностей/помилок спостереження, або із сутністю досліджуваного явища. Статистичні графіки бувають: діаграми(лінійні, радикальні, секторні, стовпчикові, стрічкові, фігурні, комбіновані), статистичні карти( картограмами, картодіаграми), графіки для аналізу раядів розподілу( гістограми, огіва, полігон, кумулята, крива Лоренца)
21. Параматри рівняння парної лінійної регресії
Парний регресійний аналіз – вид регресійного аналізу, що включає у себе розгляд однієї незалежної змінної величини, а багатофакторний – відповідно дві величини і більше. Найпростішим рівнянням парної регресії, що описує лінійну залежність між факторною і результативною ознаками, є рівняння прямої, яке має такий вигляд:
,
![]()
де
![]() –
залежна змінна, яка оцінюється або
прогнозується (результативна ознака);
–
залежна змінна, яка оцінюється або
прогнозується (результативна ознака);
![]() –
вільний
член рівняння;
–
вільний
член рівняння;
 –
коефіцієнт
регресії;
–
коефіцієнт
регресії;
х – незалежна змінна (факторна ознака), яка використовується для визначення залежної змінної.
Параметри рівняння обчислюються на основі системи нормальних рівнянь методом найменших квадратів:
![]()
Звідси
![]()
![]() ,
,
або
![]()
24. Показники динаміки. Ланцюговий та базисний способи розрахунку
Для аналізу рядів динаміки використовують показники зміни рівнів динамічного ряду, які визначають зміни, що відбуваються у досліджуваному явищі і вказують на напрям, швидкість та інтенсивність такої зміни. Ці показники отримують в результаті зіставлення рівнів ряду.
Можливі 2 варіанти зіставлення поточних рівнів ряду:
З одним і тим самим рівнем (базою) – у такому випадку отримаємо базисні показники, а за базу найзручніше брати 1-ий рівень ряду;
З попереднім рівнем ряду – в такому випадку отримаємо ланцюгові показники.
