1. Построить функции плотности вероятностей диагностического признака для исправного и неисправного состояний.
2. На основе данных о сопротивлении измерительных катушек методом Неймана-Пирсона отсортировать измерительные устройства на два состояния: – исправное состояние, – неисправное состояние. На графике из п. 1 отобразить граничное значение диагностического признака, а также зону неопределенности.
3. Повторить п. 2 по с учетом зоны неопределенности при и . На графике из п. 1 отобразить граничные значения диагностического признака, а также зону неопределенности.
4. Для п. 2 выполнить расчет вероятностей ложной тревоги и пропуска дефекта.
5. Результаты вычислений свести в таблицы. Сделать выводы.
ЗАДАНИЕ 2. Линейные методы разделения
После обследования системы по диагностическим признакам X и Y при диагнозах D1 и D2 получены значения указанных признаков (таблица). Требуется построить разделяющую поверхность в пространстве признаков.
Таблица – Значения диагностических признаков
X1 |
Y1 |
X2 |
Y2 |
1,435078 |
1,076239 |
4,970472 |
2,599426 |
1,737237 |
2,29646 |
4,430288 |
3,724942 |
1,496506 |
2,426908 |
4,882779 |
3,739253 |
2,656624 |
2,016047 |
6,225106 |
3,710343 |
1,463663 |
0,238712 |
5,569891 |
2,224824 |
Содержание отчета по заданию 2:
– график с изображением областей диагнозов;
– вычисления по всем приближениям в процессе построения разделяющей поверхности;
– графики разделяющих поверхностей (в случае их отличия от уже построенных);
– график результирующей разделяющей плоскости.
Вариант №12
ЗАДАНИЕ 1. Методы статистических решений.
При диагностировании электромагнитного измерительного устройства установлено, что в 20% случаев выход подобных устройств связаны с неисправностью измерительной катушки. При этом для исправного состояния среднее значение сопротивления катушки составляет , а среднеквадратичное отклонение . В случае наличия недопустимых изменений в измерительном сигнале среднее значение сопротивления составляет , а среднеквадратичное отклонение .
Выполнено измерение сопротивление измерительных катушек чувствительных элементов: , , , , , , , , , .
1. Построить функции плотности вероятностей диагностического признака для исправного и неисправного состояний.
2.
На основе данных о сопротивлении
измерительных катушек методом минимального
риска отсортировать измерительные
устройства на два состояния:
– исправное состояние,
– неисправное состояние. При этом
стоимость ложной тревоги и цена пропуска
дефекта соответственно составляют
и
.
Сортировку осуществлять при наличии
зоны неопределенности:
.
На графике из п. 1 отобразить граничные
значения диагностического признака.
3.
Повторить п. 2 по методу Неймана-Пирсона
при
,
.
4.
Для п. 3 построить зависимость ширины
зоны неопределенности от величины
.
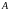4. Результаты вычислений свести в таблицы. Сделать выводы.
ЗАДАНИЕ 2. Линейные методы разделения
После обследования системы по диагностическим признакам X и Y при диагнозах D1 и D2 получены значения указанных признаков (таблица). Требуется построить разделяющую поверхность в пространстве признаков.
Таблица – Значения диагностических признаков
X1 |
Y1 |
X2 |
Y2 |
3,741196 |
-2,3526 |
6,104809 |
0,367956 |
3,620888 |
-4,59099 |
4,198537 |
-0,06395 |
3,995546 |
-2,02514 |
4,935504 |
1,143629 |
3,6662 |
-2,37436 |
4,948912 |
1,406175 |
3,911605 |
-4,17603 |
4,171643 |
0,989052 |
Содержание отчета по заданию 2:
– график с изображением областей диагнозов;
– вычисления по всем приближениям в процессе построения разделяющей поверхности;
– графики разделяющих поверхностей (в случае их отличия от уже построенных);
– график результирующей разделяющей плоскости.
Вариант №13
ЗАДАНИЕ 1. Методы статистических решений.
При диагностировании электромагнитного измерительного устройства установлено, что в 10% случаев выход подобных устройств связаны с неисправностью измерительной катушки. При этом для исправного состояния среднее значение сопротивления катушки составляет , а среднеквадратичное отклонение . В случае наличия недопустимых изменений в измерительном сигнале среднее значение сопротивления составляет , а среднеквадратичное отклонение .
Выполнено измерение сопротивление измерительных катушек чувствительных элементов: , , , , , , , , , .