1. Построить функции плотности вероятностей диагностического признака для исправного и неисправного состояний.
2. На основе данных о сопротивлении измерительных катушек методом минимального количества ошибочных решений отсортировать измерительные устройства на два состояния: – исправное состояние, – неисправное состояние. При этом стоимость ложной тревоги и цена пропуска дефекта соответственно составляют. На графике из п. 1 отобразить граничное значение диагностического признака.
3.
Повторить п. 2 по методу Неймана-Пирсона
с учетом зоны неопределенности:
,
.
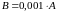4. Выполнить п. 2 методом наибольшего правдоподобия.
5. Результаты вычислений свести в таблицы. Сделать выводы.
ЗАДАНИЕ 2. Линейные методы разделения
После обследования системы по диагностическим признакам X и Y при диагнозах D1 и D2 получены значения указанных признаков (таблица). Требуется построить разделяющую поверхность в пространстве признаков.
Таблица – Значения диагностических признаков
X1 |
Y1 |
X2 |
Y2 |
1,44928 |
-14,2056 |
2,425235 |
-9,52811 |
2,176359 |
-14,7162 |
2,249781 |
-5,60166 |
1,884373 |
-13,6024 |
1,63638 |
-10,3897 |
1,024397 |
-14,8336 |
-0,45354 |
-10,669 |
2,549156 |
-14,8835 |
-0,08056 |
-5,79234 |
Содержание отчета по заданию 2:
– график с изображением областей диагнозов;
– вычисления по всем приближениям в процессе построения разделяющей поверхности;
– графики разделяющих поверхностей (в случае их отличия от уже построенных);
– график результирующей разделяющей плоскости.
Вариант №7
ЗАДАНИЕ 1. Методы статистических решений.
При
диагностировании электромагнитного
измерительного устройства установлено,
что в 7% случаев выход подобных устройств
связаны с неисправностью измерительной
катушки. При этом для исправного состояния
среднее значение сопротивления катушки
составляет
,
а среднеквадратичное отклонение
.
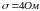В случае наличия недопустимых изменений
в измерительном сигнале среднее значение
сопротивления составляет
,
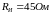а среднеквадратичное отклонение
.
Выполнено измерение сопротивление измерительных катушек чувствительных элементов: , , , , , , , , , .
1. Построить функции плотности вероятностей диагностического признака для исправного и неисправного состояний.
2.
На основе данных о сопротивлении
измерительных катушек методом минимального
риска отсортировать измерительные
устройства на два состояния:
– исправное состояние,
– неисправное состояние. При этом
стоимость ложной тревоги и цена пропуска
дефекта соответственно составляют
и
.
Требуется учесть наличие зоны
неопределенности с ценой за отказ
распознавания
.
На графике из п. 1 отобразить граничные
значения диагностических признаков, а
также зону неопределенности.
3. Повторить п. 2 по методу минимакса без учета зоны неопределенности. Привести обоснование количества приближений для расчета граничного значения диагностического параметра.
4.
Для п. 3 построить зависимость среднего
риска от соотношения
.
5. Результаты вычислений свести в таблицы. Сделать выводы.
ЗАДАНИЕ 2. Линейные методы разделения
После обследования системы по диагностическим признакам X и Y при диагнозах D1 и D2 получены значения указанных признаков (таблица). Требуется построить разделяющую поверхность в пространстве признаков.
Таблица – Значения диагностических признаков
X1 |
Y1 |
X2 |
Y2 |
2,822942 |
3,999581 |
0,572218 |
2,025828 |
1,923564 |
3,139676 |
0,002416 |
-2,30401 |
2,865464 |
4,631123 |
0,502827 |
-0,828 |
2,170201 |
3,211679 |
0,498949 |
0,209649 |
1,214431 |
3,279135 |
0,691698 |
-0,3483 |
Содержание отчета по заданию 2:
– график с изображением областей диагнозов;
– вычисления по всем приближениям в процессе построения разделяющей поверхности;
– графики разделяющих поверхностей (в случае их отличия от уже построенных);
– график результирующей разделяющей плоскости.
Вариант №8
ЗАДАНИЕ 1. Методы статистических решений.
При
диагностировании электромагнитного
измерительного устройства установлено,
что в 30% случаев выход подобных устройств
связаны с неисправностью измерительной
катушки. При этом для исправного состояния
среднее значение сопротивления катушки
составляет
,
а среднеквадратичное отклонение
.
В случае наличия недопустимых изменений
в измерительном сигнале среднее значение
сопротивления составляет
,
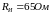а среднеквадратичное отклонение
.
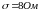Выполнено измерение сопротивление измерительных катушек чувствительных элементов: , , , , , , , , , .
1. Построить функции плотности вероятностей диагностического признака для исправного и неисправного состояний.
2.
На основе данных о сопротивлении
измерительных катушек методом минимального
риска отсортировать измерительные
устройства на два состояния:
– исправное состояние,
– неисправное состояние. При этом
стоимость ложной тревоги и цена пропуска
дефекта соответственно составляют
и
.
На графике из п. 1 отобразить граничное
значение диагностического признака.
3. Повторить п. 2 по методу минимакса. Привести обоснование количества приближений для расчета граничного значения диагностического параметра.
4.
Построить зависимость среднего риска
от величины
.
5. Результаты вычислений свести в таблицы. Сделать выводы.
ЗАДАНИЕ 2. Линейные методы разделения
После обследования системы по диагностическим признакам X и Y при диагнозах D1 и D2 получены значения указанных признаков (таблица). Требуется построить разделяющую поверхность в пространстве признаков.
Таблица – Значения диагностических признаков
X1 |
Y1 |
X2 |
Y2 |
1,222016 |
2,368177 |
0,481457 |
-2,307 |
1,439241 |
-0,14951 |
0,148289 |
-1,26973 |
1,705759 |
4,489303 |
0,059403 |
-2,28768 |
1,273843 |
-0,16842 |
0,615775 |
-1,36823 |
1,919404 |
0,484173 |
0,62051 |
1,523475 |
Содержание отчета по заданию 2:
– график с изображением областей диагнозов;
– вычисления по всем приближениям в процессе построения разделяющей поверхности;
– графики разделяющих поверхностей (в случае их отличия от уже построенных);
– график результирующей разделяющей плоскости.
Вариант №9
ЗАДАНИЕ 1. Методы статистических решений.
При диагностировании электромагнитного измерительного устройства установлено, что в 30% случаев выход подобных устройств связаны с неисправностью измерительной катушки. При этом для исправного состояния среднее значение сопротивления катушки составляет , а среднеквадратичное отклонение . В случае наличия недопустимых изменений в измерительном сигнале среднее значение сопротивления составляет , а среднеквадратичное отклонение .
Выполнено измерение сопротивление измерительных катушек чувствительных элементов: , , , , , , , , , .