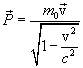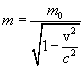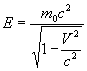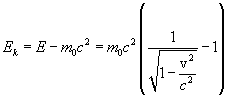6) Релятивистский импульс , основной закон релятивистской динамики

Релятивистский импульс

Уравнения классической механики инвариантны по отношению к преобразованиям Галилея, по отношению же к преобразованиям Лоренца они оказываются неинвариантными. Из теории относительности следует, что уравнение динамики, инвариантное по отношению к преобразованиям Лоренца, имеет вид:

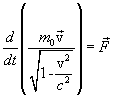
где - инвариантная, т.е. одинаковая во всех системах отсчета величина называемая массой покоя частицы, v- скорость частицы, - сила действующая на частицу. Сопоставим с классическим уравнением

Мы приходим к выводу, что релятивистский импульс частицы равен

(6.7)

Релятивистская масса.

Определив массу частицы m как коэффициент пропорциональности между скоростью и импульсом, получим, что масса частицы зависит от ее скорости.

(6.8)

Энергия в релятивистской динамике.

Для энергии частицы в теории относительности получается выражение:

(6.9)

Из (2.3) следует, что покоящаяся частица обладает энергией

(6.10)

Эта величина носит название энергии покоя частицы. Kинетическая энергия, очевидно, равна

(6.11)

Приняв во внимание, что , выражение для полной энергии частицы можно написать в виде

(6.12)

Из последнего выражения вытекает, что энергия и масса тела всегда пропорциональны друг другу. Всякое изменение энергии тела сопровождается изменением массы тела

и, наоборот, всякое изменение массы сопровождается изменениемэнергии . Это утверждение носит название закона взаимосвязи или закона пропорциональности массы и энергии.

7) Релятивистское выражение для кинетической энергии.

Релятивистская энергия.

 

 Теорема о кинетической энергии, из ньютоновской механике, верна также и для релятивистской частицы. Необходимо только видоизменить формулу кинетической энергии частицы

 

 

                                                ,                                                     (8.1)

 

 

и получить релятивистское выражение для кинетической энергии. Воспользуемся с этой целью формулой релятивистской массы

 

 

                                        .                                            (8.2)

 

 

Подставляя сюда   и возводя в квадрат, получим

 

 

                                          .                                        (8.3)

 

 

Дифференцируя это выражение, учитывая, что масса покоя m величина постоянная, будем иметь

 

.

 

Учитывая в левой части соотношение  , получим

 

                                                                                                         (8.4)

 

 

С другой стороны, формулу работы можно преобразовать следующим образом:

 

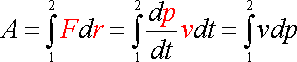
                      ,                                    (8.5)

 

 

где мы воспользовались основным уравнением релятивистской динамики

 

 

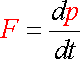
                                                                                               (8.6)

 

 

и соотношениями 

Формула (8.5), полученная для механической работы, верна как в классической, так и в релятивистской механике.  Для ее расчета необходима связь между скоростью и импульсом частицы. В релятивистской механике, учитывая формулу (8.4)  в подынтегральном выражении (8.5), будем иметь

 

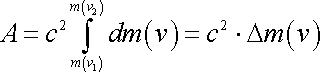
          .                                              (8.7)

 

Здесь    и   - значения массы частицы в начальном и конечном состояниях.

Значит, в релятивистской механике работа, совершенная силой, определяется только приращением релятивистской массы частицы и только ею. Если движение частицы начиналось из состояния покоя, то   и, обозначив конечную скорость через  , для работы (8.7) будем иметь

 

 

            .                                 (8.8)

 

 

Здесь выражен тот факт, что, согласно теореме о кинетической энергии, эта работа идет на увеличение кинетической энергии частицы. Учитывая в (8.8) нормировку кинетической энергии: в состоянии покоя  , получим

 

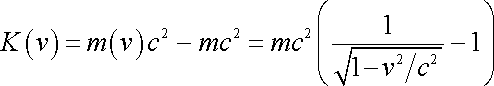
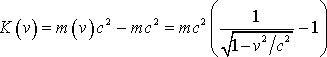.                        (8.9)

 

 

Это и есть формула релятивистской кинетической энергии. В случае малых скоростей, разложив выражение знаменателя формулы (8.9) в ряд по  степеням малой величины  :

 

                                                 

             

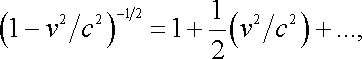
и пренебрегая членами порядка выше  , из (8.9) получим ньютоновское выражение кинетической энергии (8.1).