4) Относительность понятий движения , теорема относительности .

Относительное движение - движение точки (или тела) по отношению к подвижной системе отсчёта перемещающейся определённым образом относительно некоторой другой, основной системы отсчёта, условно наз. неподвижной. Скорость точки в О. д. называется относительной скоростью v_oт, а ускорение — относительным ускорением w_oт. Движение всех точек подвижной системы относительно неподвижной называется в этом случае переносным движением, а скорость и ускорение той точки подвижной системы, через которую в данный момент времени проходит движущаяся точка, — переносной скоростью v_пер и переносным ускорением w_nep. Наконец, движение точки (тела) по отношению к неподвижной системе отсчёта называется сложным или абсолютным, а скорость и ускорение этого движения — абсолютной скоростью v_a и абсолютным ускорением w_a. Например, если c пароходом связать подвижную систему отсчёта, а с берегом — неподвижную, то для шара, катящегося по палубе парохода, движение по отношению к палубе будет О. д., а по отношению к берегу — абсолютным. Соответственно скорость и ускорение шара в первом движении будут v_oт и w_oт, а во втором — v_a и w_a. Движение же всего парохода по отношению к берегу будет для шара переносным движением, а скорость и ускорение той точки палубы, которой в данный момент касается шар, будут v_пео и w_пер (шар рассматривается как точка). Зависимость между этими величинами даётся в классической механике равенствами:

v_a = v_oт + v_пер, w_a = w_oт + w_пер + w_kop, (1)

где w_kop — Кориолиса ускорение. Формулами (1) широко пользуются в кинематике при изучении движения точек и тел.

В динамике О. д. называется движение по отношению к неинерциальной системе отсчёта, для которой законы механики Ньютона несправедливы. Чтобы уравнения О. д. материальной точки сохранили тот же вид, что и в инерциальной системе отсчёта, надо к действующей на точку силе взаимодействия с другими телами F присоединить т. н. переносную силу инерции J_пер = –mw_пер и Кориолиса силу инерции J_kop = –mw_kop, где m — масса точки. Тогда

mw_oт = F + J_пер + J_kop. (2)

При О. д. системы материальных точек аналогичные уравнения составляются для всех точек системы. Этими уравнениями пользуются для изучения О. д. под действием сил различных механических устройств (в частности, Гироскопов), устанавливаемых на подвижных основаниях (кораблях, самолётах, ракетах), а также для изучения движения тел по отношению к Земле в случаях, когда требуется учесть её суточное вращение.

5) Закон сложения скоростей в релятивистской механике . Понятие релятивистской массы

После того, как Эйнштейн предложил принцип эквивалентности массы и энергии, стало очевидно, что понятие массы может интерпретироваться двояко. С одной стороны, это инвариантная масса, которая — именно в силу инвариантности — совпадает с той массой, что фигурирует в классической физике, с другой — можно ввести так называемую релятивистскую массу, эквивалентную полной (включая кинетическую) энергии физического объекта:

.

где — релятивистская масса, — полная энергия объекта.

Для массивного объекта (тела) эти две массы связаны между собой соотношением:

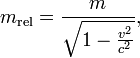
где — инвариантная («классическая») масса, — скорость тела.

Энергия и релятивистская масса — это одна и та же физическая величина (неинвариантная, аддитивная, временная компонента четырёхимпульса).

Эквивалентность релятивистской массы и энергии означает, что во всех системах отсчёта энергия физического объекта (с точностью до множителя ) равна его релятивистской массе.

Введённая таким образом релятивистская масса является коэффициентом пропорциональности между трёхмерным («классическим») импульсом и скоростью тела^[4]:

Аналогичное соотношение выполняется в классической физике для инвариантной массы, что также приводится как аргумент в пользу введения понятия релятивистской массы. Это в дальнейшем привело к тезису, что масса тела зависит от скорости его движения.

В процессе создания теории относительности обсуждались понятия продольной и поперечной массы массивной частицы (тела). Пусть сила, действующая на тело, равна скорости изменения релятивистского импульса. Тогда связь силы и ускорения существенно изменяется по сравнению с классической механикой:

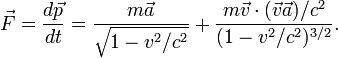
Если скорость перпендикулярна силе, то а если параллельна, то где — релятивистский фактор. Поэтому называют поперечной массой, а — продольной.

Утверждение о том, что масса зависит от скорости, вошло во многие учебные курсы и в силу своей парадоксальности приобрело широкую известность среди неспециалистов. Однако в современной физике избегают использовать термин «релятивистская масса», используя вместо него понятие энергии, а под термином «масса» понимая инвариантную массу (покоя). В частности, выделяются следующие недостатки введения термина «релятивистская масса»:

• неинвариантность релятивистской массы относительно преобразований Лоренца;

• синонимичность понятий энергия и релятивистская масса, и, как следствие, избыточность введения нового термина;

• наличие различных по величине продольной и поперечной релятивистских масс и невозможность единообразной записи аналога второго закона Ньютона в виде

• методологические сложности преподавания специальной теории относительности, наличие специальных правил, когда и как следует пользоваться понятием «релятивистская масса» во избежание ошибок;

• путаница в терминах «масса», «масса покоя» и «релятивистская масса»: часть источников просто массой называют одно, часть — другое.

Несмотря на указанные недостатки, понятие релятивистской массы используется и в учебной,^[ и в научной литературе. Следует, правда, отметить, что в научных статьях понятие релятивистской массы используется по большей части только при качественных рассуждениях как синоним увеличения инертности частицы, движущейся с околосветовой скоростью.

ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ

- определяет связь между значениямискорости материальной точки по отношению к разл. системам отсчёта, движущимсядруг относительно друга. В нерелятивистской физике, когда рассматриваютсяскорости, малые по сравнению со скоростью света с, справедлив законсложения скоростей Галилея:

где u и u' - скорости частицы в двух инерциалъных системах отсчётаК т К' соответственно (система К' движется относительно . со скоростью v). Если скорости движения близки к е, то ф-ла(1) неприменима и справедлив С. с. з. частной (специальной) относительноститеории:

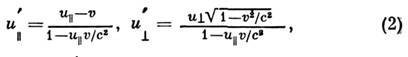
где и - проекции скорости частицы в системе отсчёта К(К' )на направления параллельное и перпендикулярное к v.В пределе и ф-лы(2) переходят в (1). В случае, когда скорости и и v параллельны,(2) переписывается в виде

Из ф-лы (3), в частности, следует, что если и = с, то и и'= с независимо от в, т. е. абс. величина скорости света не зависитот движения системы отсчёта. Тот же вывод справедлив, разумеется, и припроизвольном направлении скоростей, когда надо пользоваться ф-лой (2).

В случае неравномерных относит. движений двух систем отсчёта, а такжепри наличии тяготения (т. е. в случае общей теории относительности)все приведённые соотношения справедливы в локально сопутствующих инерциальныхсистемах отсчёта , т. е. в таких бесконечно малых системах отсчёта, к-рые в данный моменти в данном месте неподвижны относительно рассматриваемых систем К кК' соответствепно и в к-рых в этот момент нет сил ускорения и нет вращенияи деформаций, т. е. они локально инерциальны.