Задача о включении конечной линии без потерь.
Пусть линия длины
без потерь (
)
накоротко замкнута на конце
.
До начального момента напряжение и ток
в цепи отсутствовали, в начальный момент
в конце
включается источник переменного тока
с ЭДС
.
Найти
при
.
В соответствии с
выводами параграфа 3 напряжение
удовлетворяет уравнению колебаний
.
Начальные условия дают
,
.
Краевое условие на правом конце нулевое:
.
На левом конце краевое условие ненулевое:
.
Поэтому сразу невозможно применить
метод Фурье, основанный на том, что
собственные функции
или их производные должны на концах
отрезка обращаться в ноль. Сначала
ликвидируем граничную неоднородность
при помощи дополнительного слагаемого.
Ищем решение в
виде
,
где функцию
подберем так, чтобы она удовлетворяла
данным краевым условиям и уравнению
колебаний. Ищем
в виде
.
Подставляя в краевые условия, получим
.
Подставляя в уравнение колебаний,
получим
.
Решая это дифференциальное уравнение,
имеем
.
Подставляя краевые условия, получим
,
.
Отсюда
.
Поэтому вспомогательная функция,
«вбирающая в себя» краевую неоднородность
и удовлетворяющая уравнению колебаний,
после тригонометрических упрощений
принимает вид
.
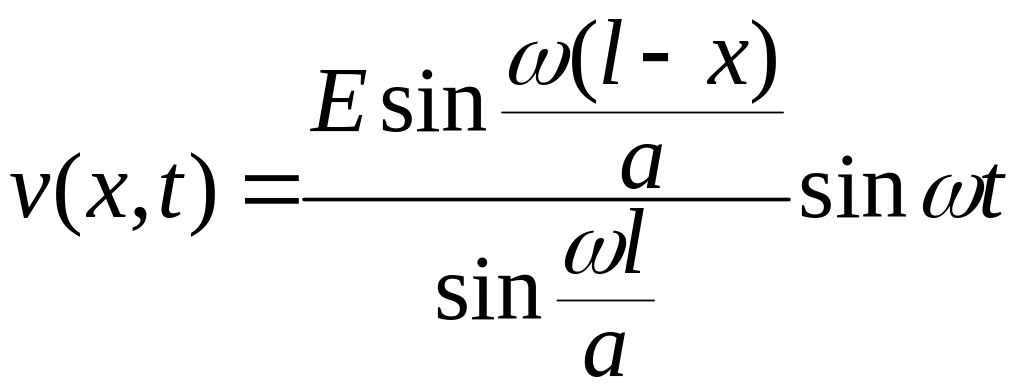Теперь на долю
второго слагаемого, функции
,
остается уравнение колебаний и нулевые
краевые условия. Начальные условия для
функции
будут равны начальным условиям для
функции
минус соответствующие начальные условия
для функции
.
Таким образом, нам предстоит найти
методом Фурье решение уравнения
,
удовлетворяющее
краевым условиям
и начальным условиям
.
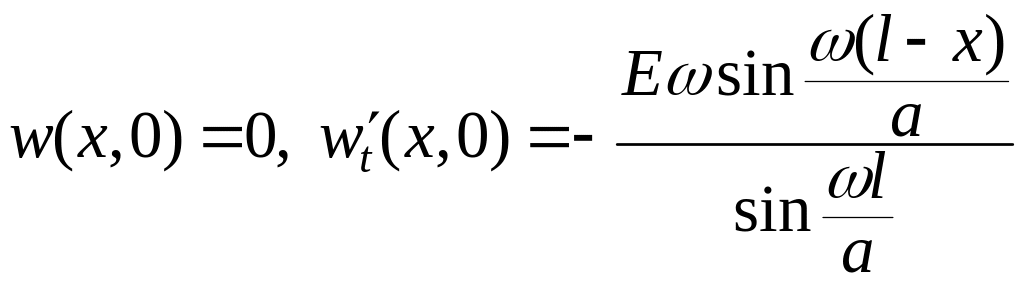Представим решение
в виде
,
где частное решение
удовлетворяет уравнению колебаний и
нулевым краевым условиям. Подставляя
в краевые условия, получим:
.
Подставляя
в уравнение колебаний, получим, разделяя
переменные уравнение
,
справедливое только в случае, если обе
части уравнения при каждом значении
равны константе. Исследуем, какой может
быть эта константа.
А) Предположим,
что
.
В этом случае, решая линейное уравнение
с постоянными коэффициентами
,
получим
.
Требуя выполнения краевых условий
,
построим для коэффициентов
и
систему
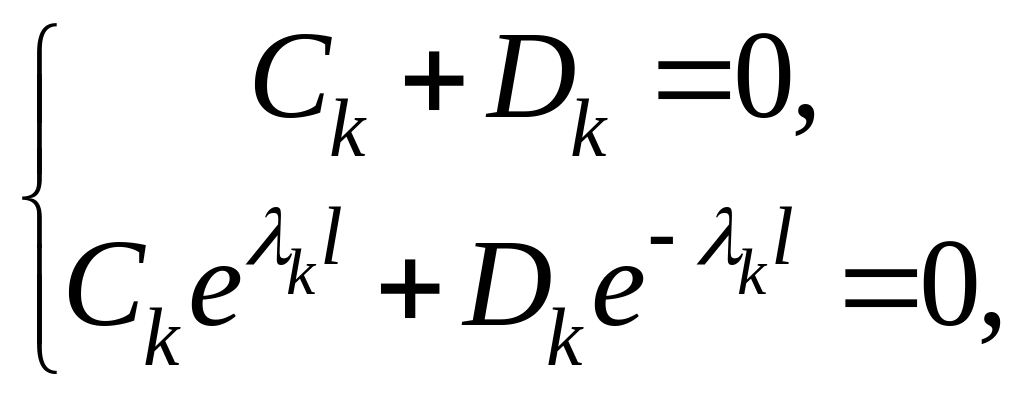имеющую только тривиальные решения.
Следовательно, предположение о том, что
привело только к нулевым частным
решениям.
Б) Предположим,
что
.
Такому уравнению удовлетворяет только
линейная функция:
.
Выполняя краевые условия, получим
.
Таким образом, в этом случае существует
также только тривиальное решение
.
В) Предположим,
что
.
В этом случае, решая линейное уравнение
с постоянными коэффициентами
,
получим
.
Условие
дает
.
Выполняя второе краевое условие
,
приходим к равенству
.
Нетривиальное решение мы получим только
при условии, что
,
.
Решая теперь уравнение для
:
,
получим
.
В силу произвольности констант
и
частное решение можно взять в виде
,
.
Итак, решение
поставленной задачи для функции
имеет вид
.
(30)
Нам остается удовлетворить начальным условиям:
и
.
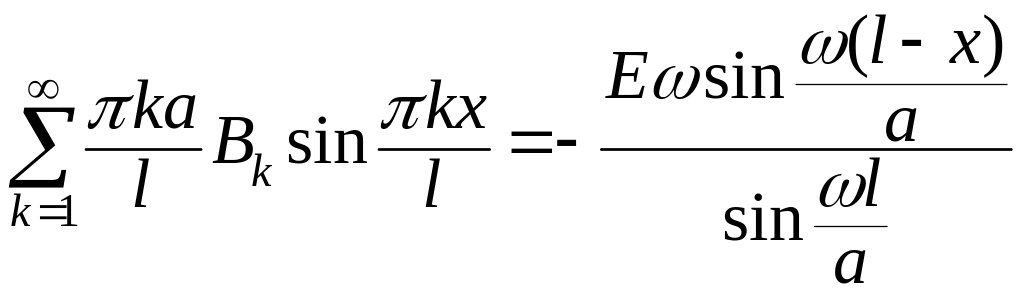Поскольку
произвольные константы оказываются
связанными с коэффициентами Фурье
разложения функции
и константы
в ряды по синусам на отрезке
,
получим
;
,
.
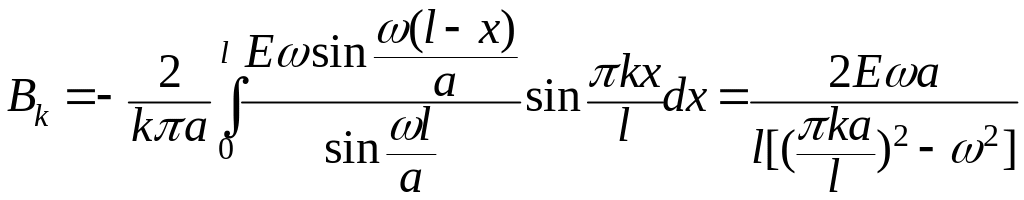Итак, остается подставить найденные константы в (30) и прибавить найденную выше функцию .