3 Законы Кирхгофа

3.1 Первый закон Кирхгофа

Определения:

Ветвью электрической цепи называется участок, состоящий из последовательно включенных источников ЭДС и приемником с одним и тем же током.

Узлом называется место или точка соединения трех и более ветвей.

Контур - замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза.

Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов, сходящихся в узле электрической цепи, равна нулю:

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Данный закон следует из закона сохранения заряда. Если цепь содержит у узлов, то она описывается у - 1 уравнениями токов. Этот закон может применяться и для других физических явлений (к примеру, водяные трубы), где есть закон сохранения величины и поток этой величины [3].

Устанавливать знаки для входящих и исходящих токов можно произвольно, но обычно придерживаются правила знаков.

Правило знаков: токи, входящие в узел, берутся со знаком «+», а выходящие из узла - со знаком «–».

3.2 Второй закон Кирхгофа

Второй закон Кирхгофа применяется к контурам и формулируется следующим образом: алгебраическая сумма падений напряжений по любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений равно нулю.

Для постоянных напряжений:

Для переменных напряжений:

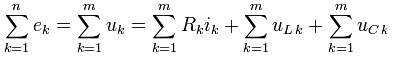
Иными словами, при обходе цепи по контуру, потенциал, изменяясь, возвращается к исходному значению. Если цепь содержит m ветвей, из которых содержат источники тока ветви в количестве m_i, то она описывается m–m_i– (у - 1) уравнениями напряжений. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи [1].

3.3 Решение по первому и второму законам Кирхгофа

Р асставляю произвольное положительное направление искомых токов в ветвях и обозначаю их на схеме, показанной на рисунке 2. Ветвь с условным обозначением вольтметра не участвует в измерениях из-за очень малых токов.

Рисунок 2 - Схема электрическая принципиальная расчетной цепи

В итоге на схеме, рисунок 2, остаётся четыре узла, так как узел есть точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка, то в этом месте есть электрическое соединение двух линий, в противном случае его нет. Узел, в котором сходятся две ветви, одна из которых является продолжением другой, называют устранимым или вырожденным узлом.

Рассчитываю количество уравнений по первому и второму закону Кирхгофа.

у = 4 – число узлов;

в = 6 – число ветвей;

в_ит = 0 – число ветвей с источником тока.

Количество уравнений по первому закону Кирхгофа n1 = у −1 = 3 Количество уравнений по второму закону Кирхгофа n2 = в − в_ит −(у − 1) = 3

Согласно первому заданию составляю системы уравнений по первому и второму законам Кирхгофа. По 1-му закону Кирхгофа для (у-1) узлов схемы, с учетом токов от источников тока, где y – число узлов схемы. Уравнение для последнего узла не составляют, т.к. оно совпало бы с уравнением, полученным при суммировании уже составленных уравнений для предыдущих узлов (т.е. линейно-независимых уравнений – (y-1)). При составлении уравнений следуют правилу: если ток выходит из узла, то его записывают со знаком «–», если входит – то со знаком «+».

Уравнения по первому закону Кирхгофа:

1. I_{4 +} I₆ – I₃ = 0 (по 1 точке)

2. I₅ – I₄ + I₂ = 0 (по 2 точке)

3. I₃ – I₁ - I₂ = 0 (по 3 точке)

Д ля составления уравнений по второму закону Кирхгофа, используется нарисованная схема, показанная на рисунке 3.

Рисунок 3 - Схема электрическая принципиальная расчетной цепи

Уравнения по второму закону Кирхгофа:

1. I₃R₃ + I₂R₂ + I₄R₄ = E₃ + E₂

2. I₁R₁ + I₅R₅ – I₂R₂ = E₁ – E₂

3. I₆R₆ – I₄R₄ – I₅R₅ = 0