4. Контрольные карты по альтернативному признаку

Часто бывает затруднительно, экономически не­оправданно или невозможно проводить измерения, необходимые для использования методов, описан­ных ранее. В настоящей главе будут рассмотрены контрольные карты, используемые при контроле ка­чества по альтернативному признаку: это значит, что после проверки изделие считается либо годным, либо дефектным и решение о качестве контролируемой совокупности принимают в зависимости от числа обнаруженных в выборке или пробе дефектных изделий или от числа дефектов, приходящихся на определенное число изделий (еди­ниц продукции).

С контролем по альтернативному признаку свя­заны понятия «дефект» и «брак».

Дефект – это каждое отдельное несоответст­вие продукции установленным требованиям.

Брак – это продукция, передача которой потребителю не допускается из-за наличия дефектов. Понятие «брак» совпадает с понятием «забракованная продукция» в тех случаях, когда продукция состоит из одной забракованной единицы или из нескольких единиц и все они забракованы.

Если совокупность единиц продукции, например партия продукции, забракована по результатам вы­борочного контроля, то в ней кроме брака могут содержаться и годные единицы продукции. Более того, в этих случаях часто доля брака оказывается малой, и ее целесообразно выделить из состава указанной совокупности.

Наиболее распространенными для метода учета дефектов являются контрольные карты доли де­фектных единиц продукции, называемые р-картами, и количества дефектов на единицу продукции, называемые с-картами. Два других вида контрольных карт этой группы – кон­трольные карты количества дефектных единиц про­дукции пр-карты и среднего числа дефектов с карты аналогичны р- и с- картам.

Понятие доли дефектных единиц продукции употребляется в том случае, когда имеется в виду до­ля дефектных единиц продукции в совокупности де­фектных и годных единиц.

Тогда p определяется следующим образом: р (доля дефектных единиц продукции) равно общему, количеству обнаруженных дефектных изделий, деленному на общее количество проверенных из­делий.

Это отношение можно представить формулой

. (1.4.1)

Иногда вместо доли дефектных единиц продук­ции используется понятие процента брака, или 100 р.

Понятие количества дефектов на единицу про­дукции используется тогда, когда изделие не счи­тается ни браком, ни годным, а определяется толь­ко количество дефектов в изделии.

Таким образом, с (количество дефектов на еди­ницу) равно общему количеству

обнаруженных де­фектов, деленному на общее количество проверен­ных изделий:

. (1.4.2)

Характеристики р и с являются статистиче­скими оценками совокупности р' и с'. Обра­тим внимание на то, что буквой d обозначается и количество дефектных изделий, и количество де­фектов, если из контекста ясно, в каком значении употребляется символ.

1. Биномиальное распределение (Теоретическое распределение доли дефектных единиц продукции при постоянных п и р)

Для того чтобы показать сущность рассматри­ваемых контрольных карт, часто используется со­суд с шариками, из которого можно извлечь вы­борку. Белые шарики считаются изделиями, кото­рые соответствуют установленным требованиям, а красные шарики имитируют дефектные изделия.

Таблица 1.4.1 – Данные для биномиального распределения р' = 0,04; n = 50

d	n	p	Марка	f
0	50	0	|||| |||| |||| |||| |||| |||| ||||	34
1	50	0,02	|||| |||| |||| |||| |||| |||| |||| |||| |||| ||||	49
2	50	0,04	|||| |||| |||| |||| |||| |||| |||| |||| |||| |||| |||| ||||	60
3	50	0,06	|||| |||| |||| |||| |||| |||| ||||	35
4	50	0,08	|||| |||| |||| |||	18
5	50	0,10	|||	3
6	50	0,12	|	1
7	50	0,14		0

Данные, приведенные в таблице 1.4.1, были получены в результате случайной выборки из сосуда, в кото­ром содержится большое количество шариков; при этом известно, что доля брака р' = 0,04. Было ото­брано 200 выборок по 50 образцов в каждой.

Столбчатая диаграмма, часто называемая гистограммой, показывает распределение долей брака. Она служит примером изменения доли дефектных единиц продукции в выборке, которое может воз­никнуть, если выборки по 50 образцов отбираются из совокупности с долей дефектных единиц продук­ции р' = 0,04.

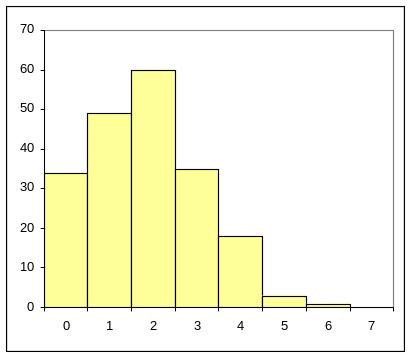
Рисунок 1.4.1 – Гистограмма данных, приведенных в таблице 1.4.1

Распределение частот, полученное таким обра­зом, является примером биномиального распределения, т.е. такого теоретического распределения, которое используется для опреде­ления положения границ регулирования контроль­ных р-карт. Укажем некоторые свойства этого рас­пределения:

1) несимметричность при р' ≠ 50;

2) предполагаемое наличие большой совокуп­ности (по меньшей мере в 10 раз больше объема выборки);

3) среднее значение ( ) величин р' в выборке наилучшим образом определяет эти величины;

4) среднее квадратическое отклонение распре­деления определяется выражением:

Его можно также приблизительно определить вы­ражением:

5) если nр' > 5, то распределение приближается к нормальному;

6) если р' < 0,1, то распределение приближается к распределению Пуассона.

Биномиальное распределение называется так потому, что если (q'+p')ⁿ разлагается по форму­ле бинома Ньютона, то последовательные члены разложения определяют вероятность появления одного, двух или п дефектных изделий в выборке. Выражение q' = 1 – р' иногда называют резуль­тативной долей.

Предположим, например, что р' = 0,2; n = 3. Тогда

(0,8+0,2)³=(0,8)²+3(0,8)²(0,2)+3(0,8)(0,2)²+. +(0,2)³=0,512+0,384+0,096+0,008

или:

Р для нуля дефектных изделий равно 0,512;

Р для одного дефектного изделия равно 0,384;

Р для двух дефектных изделий равно 0,096;

Р для трех дефектных изделий равно 0,008.

Для биномиального распределения имеются таб­лицы, рассчитанные для мно­гих значений р' и п.

Для задач контроля качества распространенной является ситуация с малой долей дефектности р' и большими объемами выборки п. В этих условиях на производстве обычно используется распределение Пуассона (Приложение 2).

Вычисление координат границ регулирования ино­гда осуществляется приближенными методами; при этом возможны случаи, когда для нижних границ регулирования получаются отрицательные значения. Такие результаты являются следствием некоррект­ного применения приближенных методов. Посколь­ку доля дефектности — не отрицательная величина, при получении отрицательных значений координат нижних границ регулирования их принимают рав­ными нулю. С целью упрощения определения коор­динат границ регулирования в приложении (уч. пособие, часть 1) приве­дена таблица 10, в которой содержатся их значения для часто встречающихся случаев. При пользовании этой таблицей не рекомендуется проводить линей­ную интерполяцию. Если же появляется острая не­обходимость в интерполяции, то применяют специ­альную бумагу с повторной логарифмической сеткой. Пользование этой бумагой сопряжено с определенными трудностями, которые преодолеваются разными методами.

2. р-карты для выборок постоянного объема

Таблица 1.4.2 – Данные для р-карты

Номер выборки	n	d	p
1	50	2	0,04
2	50	3	0,06
3	50	1	0,02
4	50	2	0,04
5	50	2	0,04
6	50	0	0
7	50	1	0,02
8	50	1	0,02
9	50	4	0,08
10	50	1	0,02
11	50	0	0
12	50	3	0,06
13	50	1	0,02
14	50	1	0,02
15	50	0	0
16	50	0	0
17	50	5	0,10
18	50	1	0,02
19	50	4	0,08
20	50	2	0,04
Итого	1000	34

ВГР = 0,034 + 0,077 = 0,111 или 11,1%

НГР = 0,034 – 0,077 = 0

Данные, приведенные в таблице 1.4.2, показывают результат 20 выборок (50 образцов каждая) из сосуда, в котором имеется 4 % красных шариков (дефектных единиц продукции). Эти выборки имитируют ежедневную выборку из процесса, продолжающегося в течение месяца. Значения р последовательно наносятся на р-карту (рисунок 1.4.2).

Центральная линия на р-карте определяет значения или среднюю долю дефектных единиц продукции. Величина равна общему количеству дефектных изделий, деленному на общее количество проверенных изделий: . Это значение р можно получить, рассчитав среднее значение всех р, однако если объем выборки не постоянный, то таким способом его вычислить нельзя. А указанная выше формула всегда справедлива.

Рисунок 1.4.2 – р-карта для данных, указанных в таблице 1.4.2

Границы регулирования определяются по формуле:

. (1.4.3)

Если на р-карте по результатам статистического контроля ни одна точка не находится вне границ регулирования, то процесс считается налаженным; при этом все отклонения точек от центральной линии являются случайными.

Если впоследствии какая-либо точка оказывается вне границ регулирования, то это значит, что появилась определенная причина разладки процесса.

Таблица 1.4.3 – Данные для расширенной р-карты

Номер выборки	n	d	p
21	50	3	0,06
22	50	4	0,08
23	50	6	0,12
24	50	9	0,18
25	50	2	0,04
26	50	6	0,12
27	50	4	0,08
28	50	3	0,06
29	50	5	0,10
30	50	4	0,08
Итого	500	46
31	50	0	0
32	50	1	0,02
33	50	0	0
34	50	0	0
35	50	1	0,02
36	50	0	0
37	50	3	0,06
38	50	2	0,04
39	50	1	0,02
40	50	1	0,02
Итого	500	9

Чтобы продемонстрировать чувствительность р-карты, возьмём выборки 21-30 из сосуда с шариками, в котором содержится 9 % дефектных единиц, а также выборки 31-40 из сосуда, в котором содержится 2 % дефектных единиц продукции. Дан­ные, полученные по этим выборкам, приведены в таблице 1.4.3.

Надо учитывать следующие важные факторы.

1. Если точка на карте оказывается выше верхней границы регулирования, то это означает, что процесс разлажен, поскольку увеличилась доля де­фектных единиц продукции. Нужно найти причины этого явления и устранить их.

2. Если точка на карте оказывается ниже нижней границы регулирования, то это значит, что процесс налажен, но его ход изменился в лучшую сторону. Выявленную причину этого необходимо использовать для совершенствования технологического про­цесса.

3. Если р-карта имеет нулевую нижнюю границу регулирования, то обнаружить определенные причины тенденции к улучшению хода процесса нельзя. Доля дефектных единиц р не отрицательная вели­чина, и ниже нулевой линии точки не могут находиться. В этом случае особенно важно следить за всеми точками, находящимися ниже центральной линии.

4. Следует отметить, что приведенный выше пример относится только к выборкам одного и того же объема. Если объем выборки изменяется, то нужно использовать р-карту для выборок переменного объема, которая приводится на рисунке 1.4.4.

5. Обратим внимание на недостаточную чувствительность р-карт. В выборках 21-30 доля дефектных изделий увеличилась с 4 до 9%, однако 7 из 10 точек находятся в пределах границ регулирования

3. np-карты для выборок постоянного объема

|Если объем выборок постоянный, то доля дефектных единиц продукции пропорциональна количеству дефектных изделий. Поэтому на одну и ту же карту можно нанести шкалу по вертикали, при помощи которой определяется количество дефектных единиц в выборке (nр), а не доля дефектных единиц продукции. Это дает возможность контролеру непосредственно отмечать количество дефектных единиц продукции, а не рассчитывать их долю.

Для np-карты:

.

Верхняя граница регулирования ;

Центральная линия ;

Нижняя граница регулирования .

Контрольная np-карта иногда называется d-картой. По данным, приведенным в таблице 1.4.2, получим значения для np-карты и построим ее, как показано на рисунке 1.4.3.

Рисунок 1.4.3 – Карта для данных, приведенных в таблицах 1.4.2 и 1.4.3.

Верхняя граница регулирования 1,7 + 3,8 = 5,5;

Центральная линия 1,7;

Нижняя граница регулирования 1,7 – 3,8 = - 2,1.

В результате получилось отрицательное число, поэтому вместо него принимается нулевое значение. Тогда

;

.

4. р-карты для выборок переменного объема

Часто при использовании р-карты бывает удобно принимать, за выборку всю продукцию, изготовленную за единицу времени, например, за час, день или неделю. В этом случае объем выборки будет непостоянным. Поскольку зависит от n, границы регулирования будут изменяться с изменением объема выборки. Рассмотрим несколько методов, используемых в подобной ситуации:

1) Границы регулирования для каждой точки на контрольной карте.

Используются следующие данные:

верхняя граница регулирования ;

центральная линия ;

нижняя граница регулирования .

Таблица 1.4.4 – Данные для р-карты при переменном объеме выборки

Номер партии	Количество проверенных образцов	Число дефектов	Доля дефектных единиц продукции	Границы регулирования
				Нижняя	Верхняя
1	100	3	0,030	0	0,1000
2	50	5	0,100	0	0,1245
3	200	8	0,040	0	0,0826
4	150	9	0,060	0	0,0891
5	50	2	0,040	0	0,1245
6	250	9	0,036	0,0032	0,0782
7	150	5	0,033	0	0,0891
8	100	4	0,040	0	0,1000
9	200	7	0,035	0	0,0826
10	250	11	0,044	0,0032	0,0782
11	50	1	0,020	0	0,1245
12	150	9	0,060	0	0,0891
13	200	5	0,025	0	0,0826
14	100	4	0,040	0	0,1000
15	250	11	0,044	0,0032	0,0782
16	50	2	0,040	0	0,1245
17	150	4	0,027	0	0,0891
18	200	8	0,040	0	0,0826
19	250	12	0,048	0,0032	0,0782
20	100	3	0,030	0	0,1000
Итого	3000	122

.

Формула для расчета :

n = 50:

n = 100:

n = 150:

n = 200:

n = 250:

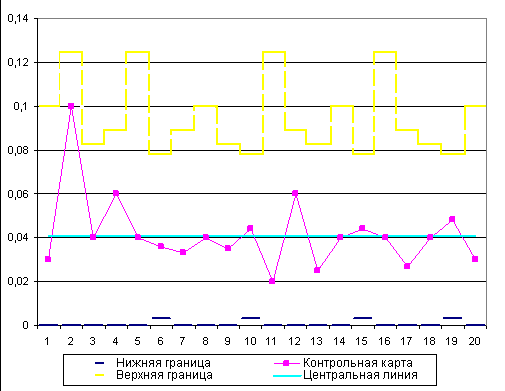
Рисунок 1.4.4 – р-карта для данных, приведенных в таблице 1.4.4

Границы регулирования рассчитываются отдель­но для каждой точки на контрольной карте, как показано в таблице 1.4.4.

Следует отметить, что если объем выборки изме­няется, то р нельзя определить при помощи расчета средних значений р; его можно определить, разделив общее количество дефектных изделий на общее количество проверенных изделий. Отметим также, что когда объем выборки изменяется, конт­рольную nр-карту использовать неудобно, поскольку центральная линия и граница регулирования также изменяются.

2) Границы регулирования, рассчитанные для нескольких выборок разного объема.

Согласно этому методу по всей контрольной карте устанавливается несколько границ регулирования, которые рассчитаны для нескольких выборок разного объема; каждая точка сверяется с со­ответствующей границей регулирования. Если какая-либо точка находится вблизи своей границы регулирования, то нужно проверить граница регулироваиия для выборку данного объема.