2.4). Классифицировать квадратичную форму и матрицу Гессе .

1. Выпишем квадратичную форму – квадратичная форма положительно определена → H(x)>0

2. Выпишем квадратичную форму

– квадратичная форма положительно определена → H(x)>0

2.5). Какая последовательность {x_k}, k=0,1,2… называется минимизирующей? Привести пример минимизирующей последовательности, не сходящейся к точке минимума.

Последовательность {x_k}, удовлетворяющая требованию: (U*-мн-во точек глобального минимума)

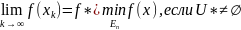
, называется минимизирующей для функции f(x).

Пример: Для функции , последовательность x^k=k является минимизирующей, но не сходится к единственной точке минимума x*=0. Напротив, минимизирующая последовательность x^k=1/k сходится к точке минимума x*=0.

2.8). Какие задачи линейного программирования можно решить графически?

Л.п. – задача нахождения экстремума функций на множестве линейных уравнений и неравенств.

Общей (основной) задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции (целевая функция) при выполнении условий: - ограничения данной задачи.

Вектор X=(x₁, x₂,…,x_n)^T, удовлетворяющий ограничениям задачи, называется допустимым решением, или планом. План X*=(x₁*, x₂*,…,x_n*)^T, при котором целевая функция принимает свое максимальное (минимальное) значение, называется оптимальным.

Непустое множество планов общей (основной) задачи линейного программирования называется многогранником решений. Если основная задача линейного программирования имеет оптимальный план, то максимальное значение целевая функция принимает в одной из вершин многогранника решений.

Вариант 5

2.1). Сформулировать свойства функций, удовлетворяющих на отрезке [a;b] условию Липшица.

Функция f(x) удовлетворяет на отрезке [a,b] условию Липшица, если существует такое число L>0 (константа Липшица), что |f(x’)-f(x”)|≤L|x’-x”| для всех x’ и x”, принадлежащих [a,b].

Из условия Липшица следует непрерывность f(x) на отрезке [a,b]. Поэтому, согласно теореме Вейерштрасса, функция f(x), удовлетворяющая на отрезке [a,b] условию Липшица, имеет на нем хотя бы одну точку минимума, хотя не является унимодальной.

Если функция f(x) имеет на отрезке [a,b] непрерывную производную, то она удовлетворяет на этом отрезке условию Липшица с константой .

2.2). Требуется найти точку минимума унимодальной функции на отрезке длины 1 с точностью ε=0,02. Имеется возможность измерить не более 10 значений f(x). Какой из прямых методов минимизации можно использовать для этого?

Число итераций, необходимое для достижения заданной точности ε на отрезке [a;b] в методе золотого сечения определяется формулой . Количество вычислений функции N=n+1=8. Ответ: можно использовать метод золотого сечения.

2.3). Сформулировать достаточные условия сходимости метода Ньютона.

f(x) − трижды непрерывно дифференцируемая выпуклая функция, разложим f(x) в ряд Тейлора в окрестности точки x_k,, x*-искомый корень:

.

Разделим на f”(x_k): , отсюда следует оценка: