Нижегородский государственный технический университет им. Р. Е. Алексеева.

Кафедра «фтос» Курсовая работа по курсу «Информатика (спец. Главы)» «Решение систем линейных уравнений методом Гаусса-Зейделя»

Выполнил: студент гр. 11-ОСС Курзенков М. И.

Проверил: Малахов В.А.

Нижний Новгород. 2012 год.

Содержание

1. Теория ………………………………………………………………… 3

2. Описание программы ……………………………………………….... 7

1. Язык программирования, среда программирования, операционная система…………………………………………….. 7

2. Блок схема……………………………………………………. 7 – 8

3. Интерфейс………………………………………………………… 8

4. Принцип работы…………………………………………………. 9

3. Листинг программы…………………………………………………... 13

4. Проверка результатов………………………………………………… 17

Решение систем линейных уравнений методом Гаусса - Зейделя.

Теория.

Одним из самых распространенных итерационных методов, отличающийся простотой и легкостью программирования, является метод Гаусса – Зейделя.

Проиллюстрируем сначала этот метод на примере системы

,

, (4.27)

,

Предположим, что диагональные элементы отличны от нуля (в противном случае можно переставить уравнение). Выразим неизвестные соответственно из первого, второго и третьего уравнений системы (4.27):

(4.28)

(4.29)

(4.30)

Зададим некоторые начальные (нулевые) приближения значений неизвестных: Подставляя эти значения в правую часть выражения (4.28), получаем новое (первое) приближение для

Используя это значение для находим из (4.29) первое приближение для

И наконец, используя вычисленные значения

с помощью выражения (4.30) первое приближения для

На этом заканчивается первая итерация решения системы (4.28) – (4.30). Используя теперь значения можно таким же способом провести вторую итерацию, в результате которой будут найдены вторые приближения к решению: и т.д.

Приближения с номером k можно вычислить, зная приближения с номером k – 1, как

Итерационный процесс продолжается до тех пор, пока значения

П р и м е р. Решить с помощью метода Гаусса – Зейделя следующую систему уравнений:

Легко проверить, что решение данной системы следующее:

Р е ш е н и е. Выразим неизвестные соответственно из первого, второго и третьего уравнений:

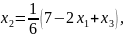
В качестве начального приближения (как это обычно делается) примем Найдем новые приближения неизвестных:

Аналогично вычислим следующие приближения:

Итерационный процесс можно продолжать до получения малой разности между значениями неизвестных в двух последовательных итерациях.

Рассмотрим теперь систему из n линейных уравнений с n неизвестными. Запишем ее в виде

Здесь также будем, предполагать, что все диагональные элементы отличны от нуля. Тогда в соответствии с методом Гаусса – Зейделя k-е приближение к решению можно представить виде

(4.31)

Итерационный процесс продолжается до тех пор, пока все значения не станут близкими к , т.е. в качестве критерия завершения итераций используется одно из условий (4.21) – (4.23), (4.24).

Для сходимости итерационного процесса (4.31) достаточно, чтобы модули диагональных коэффициентов для каждого уравнения системы были не меньше сумм модулей всех остальных коэффициентов (преобладание диагональных элементов):

При этом хотя бы для одного уравнения неравенство должно выполняться строго. Эти условия являются достаточными для сходимости метода, но они не являются необходимыми, т.е. для некоторых систем итерации сходятся и при нарушении условий (4.32).

Алгоритм решений системы n линейных уравнений методом Гаусса – Зейделя представлен в блок схеме на стр.7 – 8. В качестве исходных данных вводятся n, коэффициенты и правые части уравнений системы, погрешность ε, максимально допустимое число итераций M, а также начальные приближения переменных Отметим, что начальные приближения можно не вводить в компьютер, а полагать их равными некоторым значениям (например, нулю). Критерием итераций выбрано условие (4.22), в котором через δ обозначена максимальная абсолютная величина разности :

Для удобства чтения структурограммы объясним другие обозначения: k – порядковый номер итерации; i – номер уравнения, а также перемен-ного, которое вычисляется в соответствующем цикле; j – номер члена вида в правой части соотношения (4.31). Итерационный процесс прекращается либо при δ < ε, либо при k = M. В последнем случае итерации не сходятся, о чем выдается сообщение. Для завершения цикла, реализующего итерационный процесс, используется переменная l, которая принимает значения 0, 1 и 2 соответственно при продолжении итераций, при выполнении условия δ < ε и при выполнении условия k = M.