
- •Усиление приливов
- •Мощность приливных течений
- •Мощность приливного подъема воды
- •Перспективные районы строительства приливных электростанций
- •Глава 14
- •Теплообменники
- •Требования к насосным агрегатам
- •Другие практические соображения
- •Глава 15
- •Введение
- •Геофизика
- •Анализ свойств сухих горных пород и естественных водоносных пластов
- •Использование геотермальных ресурсов
- •Биологическое аккумулирование
- •Химическое аккумулирование
- •Аккумулирование тепла
- •Аккумулирование электроэнергии: свинцово-кислотные
- •Топливные элементы
- •Механическое аккумулирование
- •Передача энергии
Луна
A*f #«'
\а>
Земля
(Вид вдоль
оси вращения)
Рис. 13.1. Взаимное движение Земли и Луны.
Вращение происходит вокруг точки О
с частотой to, L'
— 4670
км
Рис. 13.2. Физическое обоснование
существования суточных и полусуточных
приливов. Упрощенное объяснение
равновесного прилива при нахождении
Луны в плоскости экватора Земли. В точке
Р
равные приливы наблюдаются 2 раза в
сутки— полусуточные приливы, (а).
Обычно Луна не лежит в экваториальной
плоскости Земли. Поэтому приливы в
точке Р возникают 1 раз в сутки — суточные
приливы, (б)
Приливы,
индуцируемые Луной. Земля
и Луна вращаются в космическом
пространстве вокруг друг друга (рис.
13.1), но так как масса Земли примерно в
100 раз больше массы Луны, то движение
Луны более очевидно. Центр этого вращения
находится в точке О, для которой
справедливо соотношение ML
= = M'L'.
Таким образом,
U
= MD
/(М'
+ М). (13.1)
Так
Отстояние
Луны от Земли поддерживается за счет
равенства гравитационного взаимодействия
и центробежной силы. Если обозначить
гравитационную постоянную G,
то
GMM'/D2
= M'L'o)2
= М
Lid2. (13.2)
321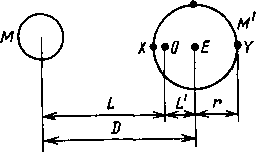

 = 4670 км, а средний радиус Земли равен
6371 км, то центр О
лежит внутри земного шара.
= 4670 км, а средний радиус Земли равен
6371 км, то центр О
лежит внутри земного шара.
Fy = m(L' + r)co2 - GMm/(D + г)2. |
(13.3) |
Для ближайшей к Луне точке X |
|
Fx = m(r — L')a>2 + GMm/(D — г)2. |
(13.4) |
По определению (см. рис. 13.1) |
|
GMm/D2 = mL' со2. |
(13.5) |
Но так как r<cD, то |
|
l/(D±r)2 = {l±2r/D)/D2. |
(13.6) |
Подставляя (13.5) и (13.6) в (13.3) и (13.4), получаем |
|
Fx = FY = mriо2(1 +2 L'/D). |
(13.7) |
Таким образом, ежедневно наблюдать два приливных |
пика с |
322
одинаковой
амплитудой. Безусловно, это имеет место
лишь в открытом океане при условии,
когда Луна находится в экваториальной
плоскости Земли.
Согласно
этой равновесной модели при малой воде
(в отлив) действующая на частицы жидкости
сила равна m/
Существуют
три принципиальные причины, по которым
действительное поведение приливов
отличается от описываемого упрощенной
моделью равновесного прилива.
Объяснение
действия приливообразующих сил в этой
модели физически корректно, однако
допущение о том, что приливный пик
может перемещаться в океане со скоростью
1600 км/ч, отслеживая вращение Земли,
ошибочно. На самом деле приливная волна
не может двигаться с такой большой
скоростью, оставаясь на меридиане
Луны (см. задачу 13.3). По мере прохождения
Луны над океаном приливное движение
распространяется всего со скоростью
500 км/ч и запаздывает по отношению к'
положению Луны. Время этого запаздывания
есть «возраст прилива». В каждом океане
образуется собственная система
вызванных Луной приливов, фазы которых
изменяются от одного океана к
другому.
Луна
обычно находится не в экваториальной
плоскости Земли (рис. 13.2, б), в результате
чего возникает суточная компонента
прилива с меньшей частотой. Существуют
и другие низкочастотные компоненты
приливного движения. Например,
расстояние между Землей и Луной
колеблется от максимального 4,06-108
м в апогее до 3,63-108
м в перигее с периодом 27,55 солнечных
суток (близким к месячному). Кроме того,
плоскость движения Луны колеблется
относительно плоскости эклиптики
системы Земля — Солнце примерно на
2°.
Большие
сложности возникают в связи с
особенностями различных океанских
бассейнов. Например, возможно образование
резонансов, особенно вблизи континентальных
шельфов, в результате которых высота
прилива существенно увеличивается. В
§ 13.3 показано, что резонансы очень
важны для создания приливных
энергетических установок.
Периодичность
лунных приливов. Для
более точного расчета периода прилива
необходимо уточнить само представление
о том, что же мы подразумеваем под
«сутками» (рис. 13.3). В точке А
на Земле солнечные сутки есть интервал
времени между двумя прохождениями
Солнца через меридиан этой точки. В
действительности этот интервал не
остается постоянным, а изменяется
в течение года из-за возмущений земной
орбиты, и, таким образом, принятая в
обиходе единица времени — средняя про-
323 2
и, таким образом, приливообразующая
сила в (13.7) есть не что иное, как т
22Ь'/D.
Можно показать (см. задачу 13.1), что
получаемый за счет этой силы
максимальный равновесный подъем воды
(равновесная высота прилива) равен 0,36
м.
2
и, таким образом, приливообразующая
сила в (13.7) есть не что иное, как т
22Ь'/D.
Можно показать (см. задачу 13.1), что
получаемый за счет этой силы
максимальный равновесный подъем воды
(равновесная высота прилива) равен 0,36
м.
Рис.
13.3. Сравнение трех различных «суток»,
наблюдаемых с Земли: звездные
и солнечные сутки (а); звездные и
лунные сутки (б). Солнечные сутки длятся
24 ч, звездные — несколько дольше,
лунные — несколько короче.
Масштабы
не соблюдены
дол
ж ител ьность сол неч ных суток tSy
определяется как интервал, осредненный
за весь год. Это и есть в точности 24
ч, т. е. /$ = 86 400 с.
Звездные
сутки — подобным образом рассчитанный
средний интервал между последовательными
прохождениями «фиксиро
ванной
звезды», т. е. настолько удаленной, что
ее видимое смещение по отношению к
Земле пренебрежимо мало. Звездные сутки
— величина, наиболее точно определяющая
период вращения Земли как бы удаленным
наблюдателем.
Из
рис. 13.3,а видно, как различие между ts
и f
связано с движением Земли вокруг Солнца
(период Ts
= 365,256 /s).
Предположим, что в полдень какого-то
известного дня центр Земли Еу
точка А
на земной поверхности, Солнце S
и некоторая фиксированная звезда
находятся на одной линии. По истечении
солнечных суток Солнце, точка А
и центр Земли снова оказываются на
одной линии. В то же время точка Е
смещается на угол 01
относительно Солнца в положение £'. Так
как ts
есть
продолжительность средних солнечных
суток, то с целью сохранения периода
мы можем представить Землю движущейся
строго по круговой орбите. В этом случае
соблюдается равенство
В
то же время точка А
поворачивается вокруг Е
на угол (2л + + 0i)
в положение А".
Время поворота на угол 2л — не что иное,
как t*
(определенное удаленным наблюдателем),
так что
Приравнивая
(13.8) и (13.9), получаем
t*
= ts/[\+(ts/Ts)]
=86 164 с = 23 ч 56 мин 4 с. (13.10)
Подобным
же образом продолжительность средних
лунных суток определяется как средний
интервал между двумя последовательными
попаданиями на одну линию центра Земли
£, точки А
и центра Луны М.
На рис. 13.3,6 показаны моменты движения
М по круговой орбите вокруг Земли. В
течение времени tM
Луна
Q\/2n
= ts/Ts.
(13.8)
01/2л=(*5-О/<*-
(13.9)
324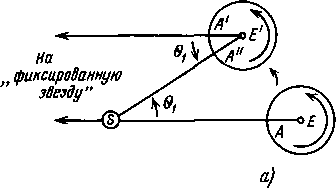

переместилась
на угол 02
из точки М
в точку М\
за то же время точка А
на поверхности Земли повернулась на
угол 2л + 02
в точку А'.
Таким образом, с точки зрения удаленного
наблюдателя
02/2я
=
tM/T*
= (tM
- /*)//*, (13.11)
где
r*
= 27,32£s
(так называемый звездный лунный месяц,
«действительный» лунный месяц) —
период вращения Луны вокруг Земли с
точки зрения удаленного наблюдателя.
Эта величина несколько менее лунного
месяца, фиксируемого наблюдателем,
находящимся на поверхности Земли (Г =
29,53 сут), в связи с вращением Земля вокруг
Солнца. Выражение (13.11) подразумевает,
что
tM
= t*/[\—(i*/T*)]
=89 428 с = 24 ч 50 мин 28 с. (13.12)
Приливы,
вызываемые Солнцем. Смешанные приливы.
С
помощью теории Ньютона объясняется
и возникновение солнечных приливов,
происходящих 2 раза в сутки с периодом,
в точности равным половине солнечных
суток. Правда, высота солнечного прилива
примерно в 2,2 раза меньше лунного,
являющегося доминирующим. Это следует
из предположения о том, что отличие
высот приливов пропорционально различию
в гравитационных силах, создаваемых
Луной и Солнцем в противоположных по
диаметру d
точках земной поверхности. Если Мм
и Ms
— массы Луны и Солнца, а расстояние от
них до Земли — соответственно DM
и Ds,
то для обеих систем гравитационные
силы пропорциональны M/D2
и различие в силах
^d=-2Md/D\ (13.13)
Отношение
высот лунного RM
и солнечного Rs
приливов пропорционально приращениям
соответствующих гравитационных сил:
(ду
Dfr) =
/ РдчЗМа,
=
Rs
(MS/D3S)
DM'
Ms
Солнечные
приливы могут возникать в фазе и в
противофазе с лунными. Если Солнце,
Земля и Луна оказываются на одной линии
— оба прилива в фазе: возникает прилив
максимальной высоты. Это случается
дважды в лунный месяц, во время полнолуния
и новолуния, называются такие приливы
сизигийными.
Когда же направления Солнце — Земля и
Земля — Луна перпендикулярны
(находятся в квадратуре), высоты суммарных
приливов минимальны (квадратурные
приливы). Подобные угасания приливов
повторяются также дважды за лунный
месяц. Если возрастание высоты прилива
— результат суммирования лунной и
солнечной составляющих, то угасание —
результат их вычитания. Отношение
высот сизигийного и квадратурного
приливов
325
можно
представить в следующем виде:
RC/RKB
=
(1 + 1 /2,2)/( 1 — 1/2,2) = 3. (13.15)
На
практике различные динамические и
локальные эффекты вызывают несоответствие
реальных приливов этой упрощенной
модели, отношение высот Rc/Rkb
чаще всего приближается к двум. Сизигийные
приливы во время перигея Луны имеют
большую высоту, чем при ее апогее, а
комбинация эффектов, включающих ветровой
нагон, может стать причиной необычайно
высоких приливов.
Обычный
прилив в открытом океане имеет высоту
менее 1 м и не пригоден для целей
энергетики. Однако вблизи ряда эстуариев
и некоторых других природных образований
высоты приливов увеличиваются. Это
может происходить за счет эффекта
воронки (напоминает усиление звуковых
волн в сужающемся канале старомодного
стетоскопа) и за счет резонансного
совпадения естественных частот движения
водных масс и соответствующих бассейнов
на побережье.
Приливное
движение в море имеет форму движущейся
волны, называемой приливной
волной.
В этой волне, длина которой довольно
велика, если сравнивать с глубиной
моря, весь столб воды от поверхности
до дна движется с одинаковой скоростью
(рис. 13.4). Движение непрерывно
распространяющейся естественной
приливной волны имеет скорость с,
связанную с ускорением силы тяжести и
глубиной моря h
соотношением c
= (gH)/l.
Естественно, что вынужденное движение
приливных волн, вызванных притяжением
Луны и Солнца, не подчиняется требованиям
условия свободного распространения
волн и что в открытом океане не происходит
резонансного усиления этого вынужденного
движения. Резонансы могут возникать
в некоторых эстуариях и заливах, однако
это не единственная причина значительных
изменений в приливном движении.
Землетрясения в толще океанского дна
или извержения подводных вулканов
могут вызвать свободно распространяющуюся
«приливную волну», называемую цунами,
но такая волна лишь по форме движения
похожа на приливную.
Вообразим
слой воды глубиной Л, шириной 6, толщиной
Дх. и с подъемом уровня поверхности над
средним положением z.
Изменение
положения уровня поверхности на толщине
Ах, равное
zf
^ z
X
Лх
Z-~h
I и
Рис. 13.4. Движение воды в при-
I 1-^.
ливной волне: и
— скорость; h
—
1
I-»- глубина
326Усиление приливов
(dz/dx)Ax,
по сравнению с z
— малая величина. Боковая поверхность
слоя имеет площадь A
= hb.
Чтобы
описать условие образования волны,
достаточно знать ньютоновское уравнение
движения жидкости для слоя и условие
сохранения ее массы. Разность давлений
на противоположных сторонах слоя,
возникающая в результате небольшого
изменения высоты подъема поверхности,
равнй
Таким
образом, уравнение движения слоя в
форме второго закона динамики Ньютона
при скорости и
имеет вид
Разность
потоков жидкости, втекающей в слой и
вытекающей из слоя, должна компенсироваться
изменением во времени его объема,
выполнение требования сохранения массы
определяется уравнением неразрывности
вида
Резонансное
усиление приливов в эстуариях и заливах
аналогично тому, как это происходит
при резонансе звуковых волн в акустических
резонаторах (рис. 13.5).
Резонанс
для приливной волны, надвигающейся со
стороны открытого моря, наступает,
когда
где
/ — нечетное целое.
Соответствующая
резонансная частота fr
и период Тг
связаны
(13.16)
(13.17)
ди
W
g
dz_
дх
’
(13.18)
[±{А
+ bz)u]
Ах =^~ =
?-[(Л
+^х].
(13.19)
Так
как A=bh
— константа и A^bz,
то
а
ди
.dz
ди
1 dz
дх
dt
’ дх h
dt
’
Из
(13.18) и (13.20) следует, что
д2и
d2z
д2и
1 d2z
dtdx ®
дх2
дхд* h
dt2
Таким
образом,
(13.20)
(13.21)
— =gh—
=
г—,
dt2 дх2
дх2
(13.22)
а
это и есть уравнение движения волны со
скоростью
c
= {gh)h.
(13.23)
L
= jX/4,
(13.24)
327![]()
![]()
![]()
g.
АЛ
Открытое
море
I
^
*777777777777/
У.
Суша
Рис. 13.5. Резонансное усиление приливной
волны в эстуарии, вид в плане.
Идеализированный залив глубиной h
и
длиной L—X/4
(четвертьволновый резонатор)
между
собой следующим образом:
fr=\/Tr
= c/k. (13.25)
Отсюда
Т
г ==Х/с = AL/j(gh)/2. (13.26)
Резонанс
возникает, когда период собственных
колебаний соответствующего бассейна
оказывается равным (кратным) периоду
вынужденных колебаний прилива в открытом
море Г/, в этом случае
= -±-=Ш/гТ,. (13.27)
(gh)1
А 4
Полусуточный
период прилива равен 12 ч 25 мин (45 000 с),
таким образом, для случая / = 1 (основная
гармоника) резонанс наступает, когда
L/ft'/2
= (45 ООО с) (9,8 м/с2)774=36
ООО м7\
(13.28)
Пример
13.1.
Эстуарий р. Северн между Уэлсом и
Великобританией имеет протяженность
около 200 км при глубине около 30 м, так
что для него
L/Л /2«36 400 м'/2. (13.29)
В
этом примере видно близкое совпадение
собственной частоты эстуария с
характерной частотой прилива, в
результате чего в указанном эстуарии
достигаются значительные амплитуды
приливного* движения, высота прилива
здесь доходит до 10—14 м.
На
практике эстуарии и заливы, конечно,
не имеют таких однозначно определенных
размеров, какие использованы в примере.
Поэтому анализ резонансных условий
сильно усложняется. Стало необходимым
проводить моделирование природных
условий в лабораторных волновых
бассейнах с использованием соответствующей
техники масштабирования и путем
теоретического анализа. Это очень
важно в связи с тем, что одним из основных
вопросов при проектировании приливных
энергоузлов является выяснение того,
как дамба и плотина будут влиять на
резонансные условия в бассейне. Некоторые
расчеты, выполненные для эстуария
р. Северн, показали возможность уменьшения
и увеличения высоты приливов в зависимости
от «размещения ПЭС. Строительство ПЭС
слишком дорого, чтобы позволить
разработчикам ошибаться.
328
