Целочисленная арифметика

1. Напечатать все простые делители заданного натурального числа

2. Определить, является ли заданное натуральное число совершенным, т. е. равным сумме всех своих (положительных) делителей, кроме самого этого числа (например, число 6 совершенно: 6=1+2+3).

3. Определить число, получаемое выписыванием в обратном порядке цифр заданного натурального числа.

4. Дано натуральное . Напечатать -ю цифру последовательности

   1. 12345678910111213..., в которой выписаны подряд все натуральные числа;

   2. 149162536..., в которой выписаны подряд квадраты всех натуральных чисел;

   3. 1123581321..., в которой выписаны подряд все числа Фибоначчи.

5. Напечатать все простые делители заданного натурального числа.

6. Дано натуральное число . Выяснить, верно ли, что равно кубу суммы цифр числа .

7. Дано натуральное число .

   1. Сколько цифр в числе ?

   2. Чему равна сумма его цифр?

   3. Найти первую цифру числа .

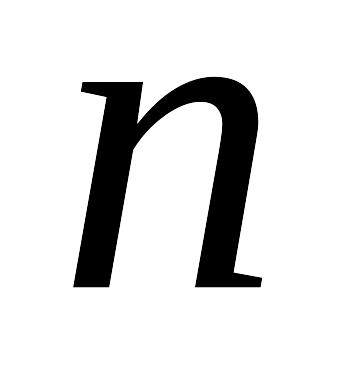   4. Найти знакочередующуюся сумму цифр числа (пусть запись в десятичной системе есть ; найти ).

8. Дано натуральное число .

   1. Является ли это число палиндромом (с учетом четырех цифр, например 2222, 6116, 0440 и т. д.)?

   2. Верно ли, что это число содержит ровно три одинаковые цифры, как, например, числа 6676, 4544, 0006 и т. д.?

   3. Верно ли, что все четыре цифры числа различны?

9. Даны целые числа , указывающие момент времени: часов, минут. Определить наименьшее время (число полных минут), которое должно пройти до того момента, когда часовая и минутная стрелка на циферблате

   1. совпадут;

   2. расположатся перпендикулярно друг к другу.

10. Доказано, что любое целое 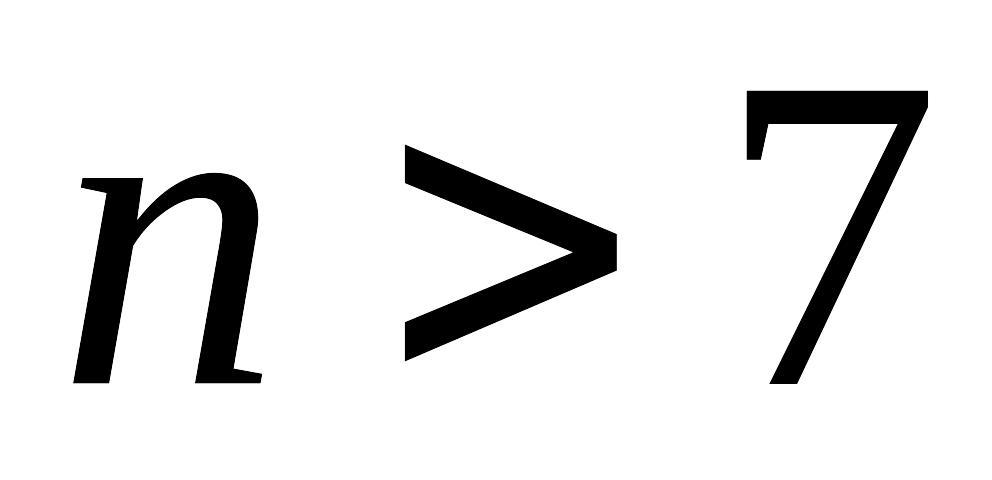можно представить в виде , где и целые неотрицательные числа. Для данного найти целые неотрицательные и .

11. Получить сумму последних цифр числа .

12. Дано натуральное число .

    1. Выяснить, входит ли цифра 3 в запись числа .

    2. Поменять порядок цифр числа на обратный.

    3. Переставить первую и последнюю цифры числа .

    4. Приписать по единице в начало и в конец записи числа .

13. Дано натуральное число _{. Выбросить из записи числа} цифры 0 и 5, оставив прежним порядок остальных цифр. Например, из числа 59015509 должно получиться 919.

14. Алгоритм Евклида нахождения наибольшего общего делителя (НОД) неотрицательных целых чисел основан на следующих свойствах этой величины. Пусть 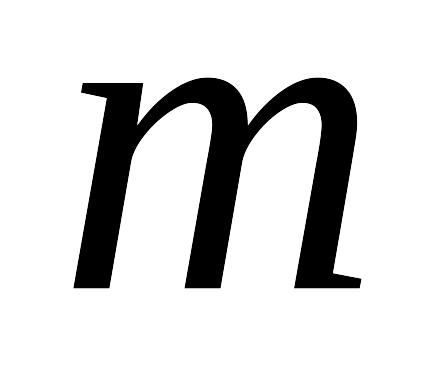и  одновременно не равные нулю целые неотрицательные числа и пусть . Тогда, если , то НОД( , )= , а если , то для чисел , и , где  остаток от деления на , выполняется равенство НОД( , )= НОД( , ). Например, НОД(15, 6)=  =НОД(6, 3)=НОД(3,0)=3. Даны натуральные числа , .

    1. Используя алгоритм Евклида, найти наибольший общий делитель и .

    2. Найти наименьшее общее кратное и . (Как здесь может помочь алгоритм Евклида)?

15. Даны натуральные числа и . Найти такие натуральные и , не имеющие общих делителей, что .

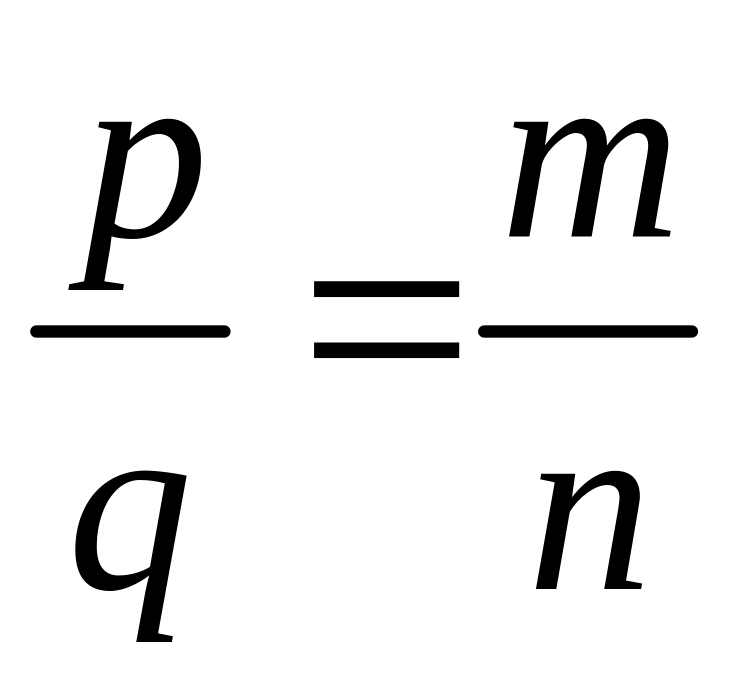16. Даны натуральные числа , 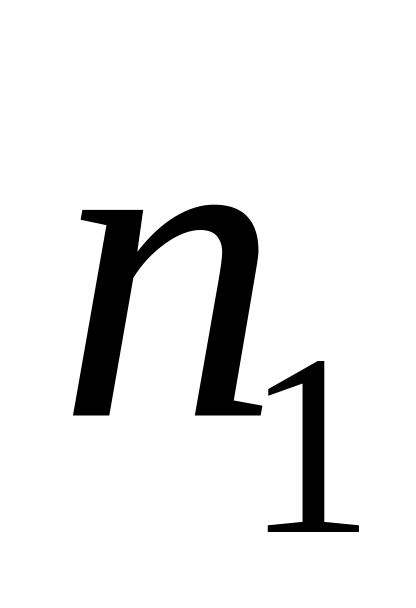,…, ( ). Вычислить НОД( ,…, ), воспользовавшись для этого соотношением НОД( ,…, )=НОД(НОД( ,…, ), ).

17. Треугольником Паскаля называется числовой треугольник

в котором по краям стоят единицы, а каждое число равно сумме двух стоящих над ним в ближайшей сверху строке. Дано натуральное . Получить первые строк треугольника Паскаля.

18. Два натуральных числа называют дружественными, если каждое из них равно сумме делителей другого, кроме самого этого числа. Найти все пары дружественных чисел, лежащих в диапазоне от 200 до 300.

19. Дано натуральное число . Среди чисел найти все такие, запись которых совпадает с последними цифрами записи их квадрата (как, например, , и т. д.).

20. Назовем натуральное число палиндромом, если его запись читается одинаково с начала и с конца (как, например, 4884, 393, 1).

    1. Найти все меньшие 100 натуральные числа, которые при возведении в квадрат дают палиндром.

    2. Найти все меньшие 100 натуральные числа  палиндромы, которые при возведении в квадрат также дают палиндромы.

21. Дано натуральное число ( ). Получить все трехзначные натуральные числа, сумма цифр которых равна .

22. Построить первые натуральных чисел, делителями которых являются только числа 2, 3 и 5.

23. Даны натуральные числа , . Получить все меньшие натуральные числа, квадрат суммы цифр которых равен .

24. Указать то число заданного множества целых чисел, в двоичном представлении которого больше всего единиц.

25. Перечислить все натуральные числа, не превосходящие заданного , в двоичном представлении которых номера ненулевых разрядов образуют арифметическую прогрессию.

26. Найти все пары двузначных натуральных чисел , таких, что значение произведения не изменится, если поменять местами цифры каждого из сомножителей (такой парой будет, например, 38 и 83).

27. Найти все натуральные числа, не превосходящие заданного и делящиеся на каждую из своих цифр.

28. Найти все натуральные числа, не превосходящие заданного , десятичная запись которых есть строго возрастающая или строго убывающая последовательность цифр.

29. Для натуральных , операцию определим так:

. Найти все такие пары , , не превосходящие заданного , для которых .